

所属成套资源:人教版八年级数学上册全套课件
人教版八年级上册11.1.2 三角形的高、中线与角平分线教课ppt课件
展开
这是一份人教版八年级上册11.1.2 三角形的高、中线与角平分线教课ppt课件,共34页。PPT课件主要包含了学习目标,导入新课,复习导入,三角形的高的定义,从三角形的一个顶点,向它的对边,所在直线作垂线,和垂足,之间的线段,叫作三角形的高线等内容,欢迎下载使用。
1.掌握三角形的高,中线及角平分线的概念.(重点)2.掌握三角形的高,中线及角平分线的画法.3.掌握钝角三角形的两短边上高的画法.(难点)
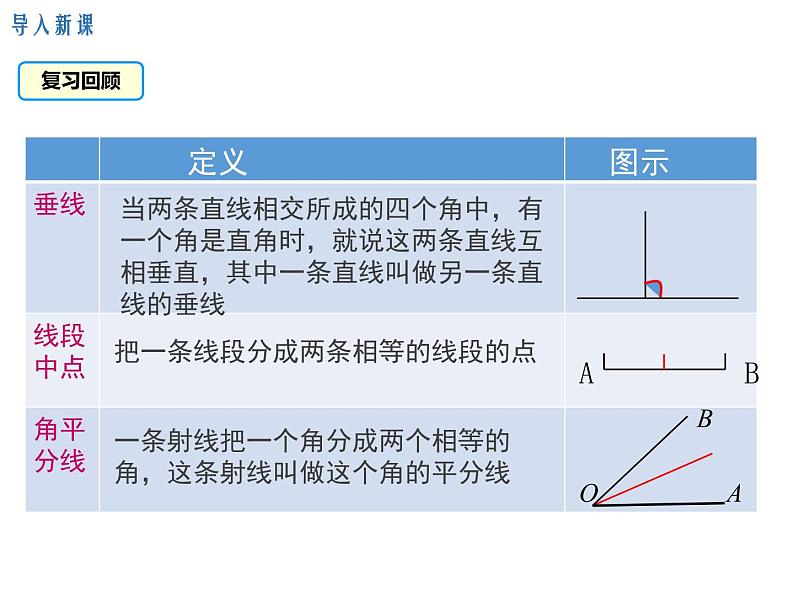
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
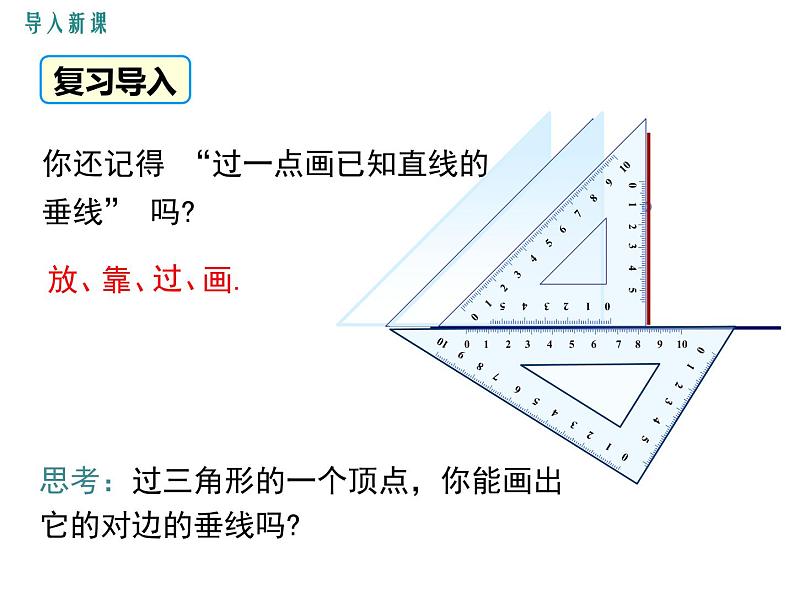
你还记得 “过一点画已知直线的垂线” 吗?
思考:过三角形的一个顶点,你能画出它的对边的垂线吗?
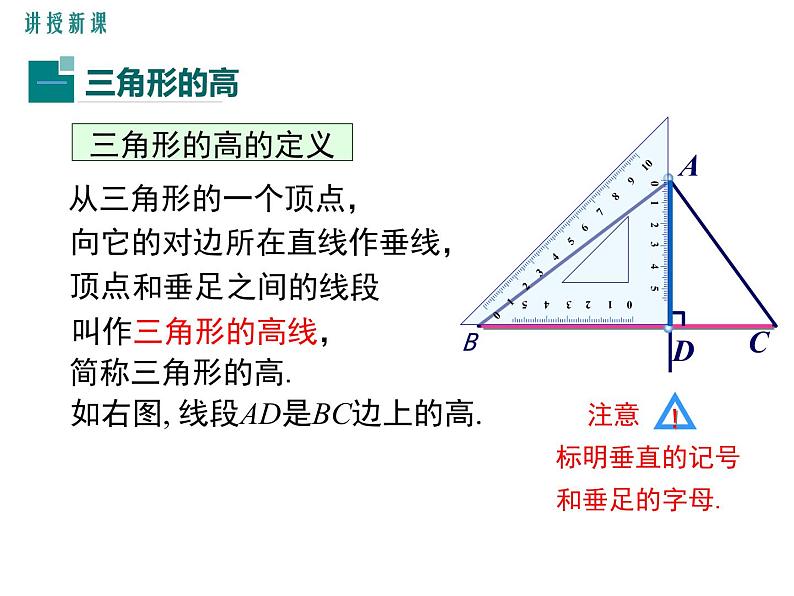
如右图, 线段AD是BC边上的高.
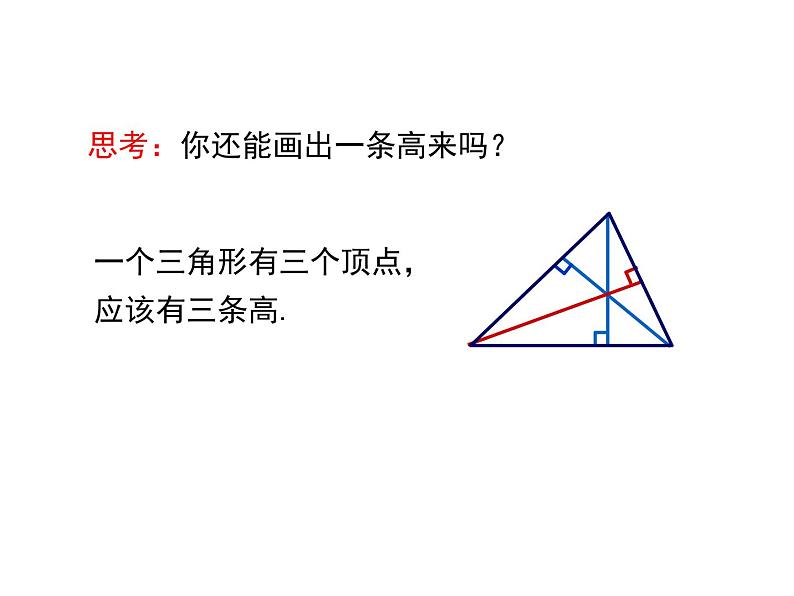
思考:你还能画出一条高来吗?
一个三角形有三个顶点,应该有三条高.
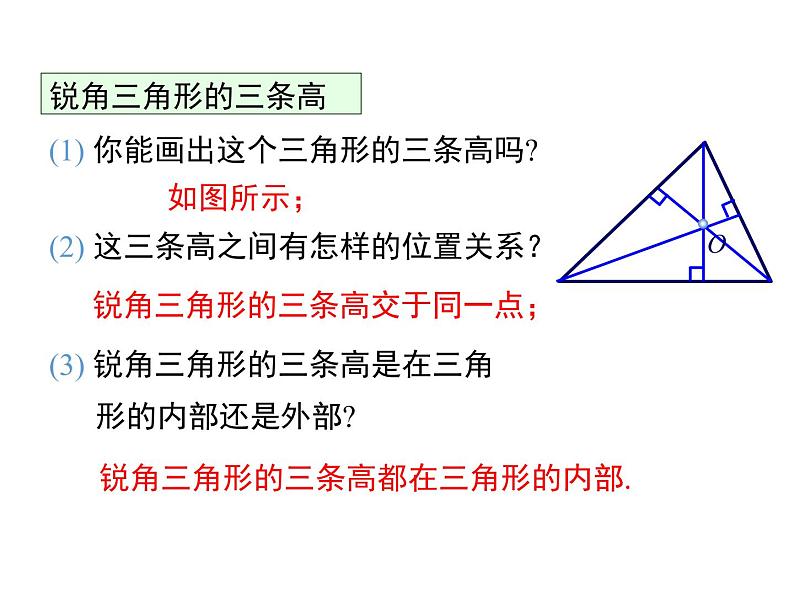
(1) 你能画出这个三角形的三条高吗?
(2) 这三条高之间有怎样的位置关系?
(3) 锐角三角形的三条高是在三角 形的内部还是外部?
锐角三角形的三条高交于同一点;
锐角三角形的三条高都在三角形的内部.
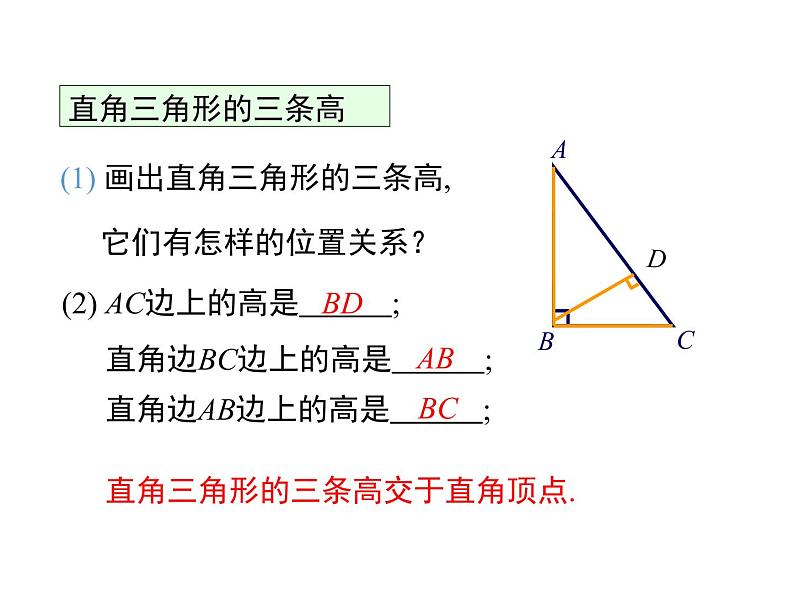
(1) 画出直角三角形的三条高,
它们有怎样的位置关系?
直角三角形的三条高交于直角顶点.
(1) 你能画出钝角三角形的三条 高吗?
(3)钝角三角形的三条高 交于一点吗?
(4)它们所在的直线交于 一点吗?
钝角三角形的三条高不相交于一点;
钝角三角形的三条高所在直线交于一点.
视频:画钝角三角形的高
例1 作△ABC的边AB上的高,下列作法中,正确的是( )
方法总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
例2 如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为____.
例3 如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
解:∵AD是△ABC的角平分线,∠BAC=60°, ∴∠DAC=∠BAD=30°.∵CE是△ABC的高,∠BCE=40°,∴∠B=50°,∴∠ADB=180°-∠B-∠BAD=180°-30°-50°=100°.
在三角形中,连接一个顶点与它对边中点的线段,叫作这个三角形的中线(median). AE是BC边上的中线.
(1)在纸上画出一个锐角三角形,确定它的中线. 你有什么方法?它有多少条中线?它们有怎样的 位置关系?
(2)钝角三角形和直角三角形的中线又是怎样的? 折一折,画一画,并与同伴交流.
三角形的三条中线交于一点,这个交点就是三角形的重心.
例4 在△ABC中,AC=5cm,AD是△ABC的中线,若△ABD的周长比△ADC的周长大2cm,则BA=________.
提示:将△ABD与△ADC的周长之差转化为边长的差.
在一张薄纸上任意画一个三角形,你能设法画出它的一个内角的平分线吗?你能通过折纸的方法得到它吗?
用量角器画最简便,用圆规也能.
在一张纸上画出一个一个三角形并剪下,将它的一个角对折,使其两边重合.
折痕AD即为三角形的∠A的平分线.
三角形的角平分线的定义:
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫三角形的角平分线.
注意:“三角形的角平分线”是一条线段.
每人准备锐角三角形、钝角三角形和直角三角 形纸片各一个. (1) 你能分别画出这三个三角形的三条角平分线吗? (2) 你能用折纸的办法得到它们吗? (3) 在每个三角形中,这三条角平分线之间有怎样的 位置关系 ?
三角形的三条角平分线交于同一点.
解:∵AD是△ABC的角平分线,∠BAC=68°, ∴∠DAC=∠BAD=34°. 在△ABD中, ∠B+∠ADB+∠BAD=180°, ∴∠ADB=180°-∠B-∠BAD =180°-36°-34°=110°.
例5 如图,在△ABC中,∠BAC=68°,∠B=36°,AD是△ABC的一条角平分线,求∠ADB的度数.
1.下列说法正确的是 ( )A.三角形三条高都在三角形内 B.三角形三条中线相交于一点C.三角形的三条角平分线可能在三角形内,也可 能在三角形外D.三角形的角平分线是射线
2.在△ABC中,AD为中线,BE为角平分线,则在以下等式中:①∠BAD=∠CAD;②∠ABE=∠CBE;③BD=DC;④AE=EC.其中正确的是 ( )A.①② B.③④ C.①④ D.②③
3.如图,△ABC中∠C=90°,CD⊥AB,图中线段中可以作为△ABC的高的有 ( )A.2条 B.3条 C.4条 D.5条
5.填空:(1)如图①,AD,BE,CF是△ABC的三条中线,则 AB= 2__,BD= __,AE= __
(2)如图②,AD,BE,CF是△ABC的三条角平分线,则∠1= __, ∠3=_________, ∠ACB=2______.
6.在ΔABC中,CD是中线,已知BC-AC=5cm,ΔDBC 的周长为25cm,求ΔADC的周长.
解:∵CD是△ABC的中线,∴BD=AD,∴△DBC的周长=BC+BD+CD=25cm,则BD+CD=25-BC.∴△ADC的周长=AD+CD+AC =BD+CD+AC =25-BC+AC =25-(BC-AC)=25-5=20cm.
7.如图,AE是 △ABC的角平分线.已知∠B=45°, ∠C=60°,求∠BAE和∠AEB的度数.
解:∵AE是△ABC的角平分线,
∵ ∠BAC+∠B+∠C=180°,
∴∠BAC=180°-∠B-∠C=180°-45°-60°=75°,∴∠BAE=37.5°.
∵∠AEB=∠CAE+∠C,∠CAE=∠BAE=37.5°,
∴∠AEB=37.5°+60°=97.5°.
8.如图,在△ABC中,AD是△ABC的高,AE是 △ABC的角平分线,已知∠BAC=82°,∠C=40°, 求∠DAE的大小.
解: ∵ AD是△ABC的高,
∵ ∠ADC+∠C+∠DAC=180°,
∴ ∠DAC=180°-(∠ADC+∠C )
=180°-90°-40°=50°.
∵AE是△ABC的角平分线,且∠BAC=82°,
∴∠DAE=∠DAC-∠CAE=50°-41°= 9°.
相关课件
这是一份数学八年级上册第十一章 三角形11.1 与三角形有关的线段11.1.2 三角形的高、中线与角平分线教学课件ppt,共21页。PPT课件主要包含了回忆与思考,用几何符号表示为,范例学习,新知运用2等内容,欢迎下载使用。
这是一份初中数学人教版八年级上册第十一章 三角形11.1 与三角形有关的线段11.1.2 三角形的高、中线与角平分线优秀ppt课件
这是一份初中11.1.2 三角形的高、中线与角平分线图文课件ppt,共60页。PPT课件主要包含了符号语言,三角形的高线定义,对边的中点,三角形的中线定义,反之如图,课堂小结,三角形的高线,三角形的中线,三角形的角平分线,课后作业等内容,欢迎下载使用。









