

【数学】北京市东城区2019-2020学年高二下学期期末统一检测试题
展开北京市东城区2019-2020学年
高二下学期期末统一检测试题
本试卷共4页,共100分。考试时长120分钟。考生务必将答案答在答题卡上,在试卷上作答无试效。考结束后,将答题卡一并交回。
第一部分(选择题共40分)
一、选择题共10小题,每小题4分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
(1) 展开式中各项系数之和为
(2)已知函数y=f(x)在处的导数为1,则
(3)若变量x,y之间是线性相关关系,则由以下数据表得到的回归直线必过定点
(A) (2,6)
(B) (3,8)
(C) (4,9)
(D)(5,10)
(4)3位老师和4名学生站成一排,要求任意两位老师都不相邻,则不同的排法种数为
(5)已知随机变量X服从二项分布,即X~B(n,p),且E(X)=2,D(X)=1.6,则二项分布的参数n,p的值为
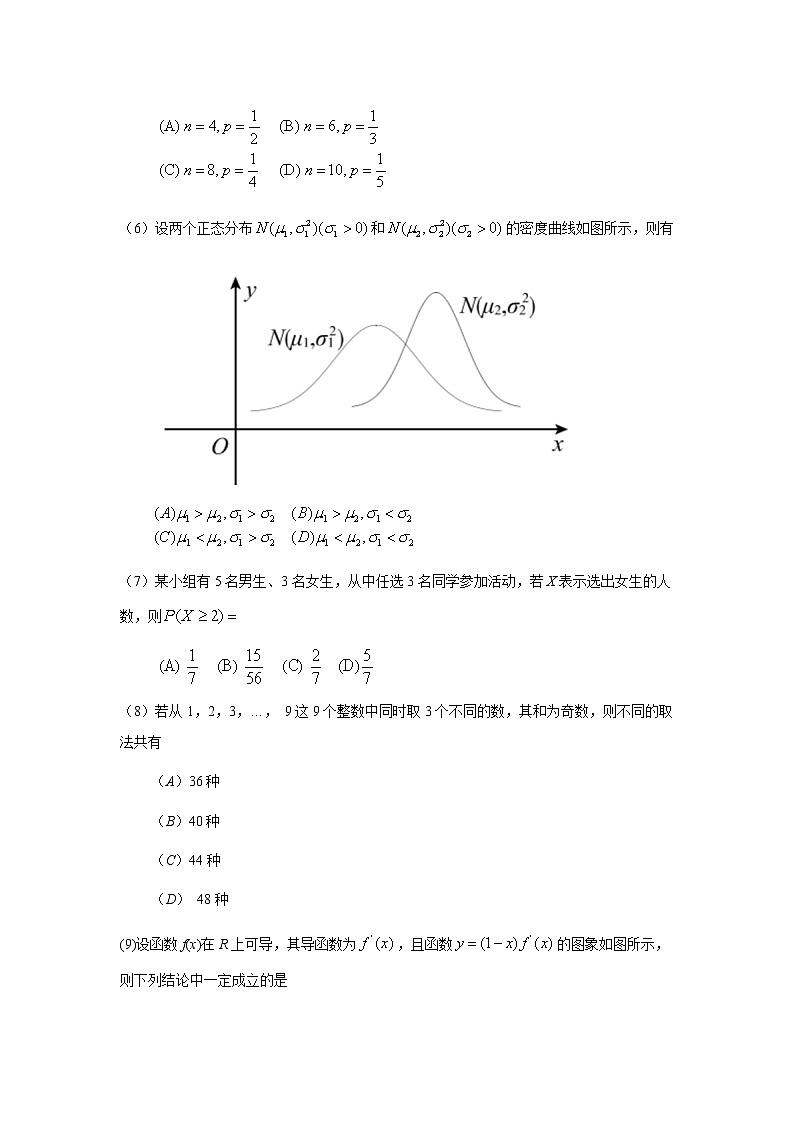
(6)设两个正态分布和的密度曲线如图所示,则有
(7)某小组有5名男生、3名女生,从中任选3名同学参加活动,若X表示选出女生的人数,则
(8)若从1,2,3,…, 9这9个整数中同时取3个不同的数,其和为奇数,则不同的取法共有
(A)36种
(B)40种
(C)44种
(D) 48种
(9)设函数f(x)在R上可导,其导函数为,且函数的图象如图所示,则下列结论中一定成立的是
(A)f(x)有极大值f(-2)
(B) f(x)有极小值f(-2)
(C)f(x)有极大值f(1)
(D)f(x)有极小值f(1)
(10)某企业拟建造一个容器(不计厚度,长度单位:米),该容器的底部为圆柱形,高为1,底面半径为r,上部为半径为r的半球形,按照设计要求容器的体积为立方米.假设该容器的建造费用仅与其表面积有关,已知圆柱形部分每平方米建造费用为3万元,半球形部分每平方米建造费用为4万元,则该容器的建造费用最小时,半径r的值为
第二部分(非选择题共60分)
二、填空题共5小题,每小题4分,共20分。
(11)在的展开式中,的系数为________(用数字作答)
(12)给出下列三个结论:
①若,则
②若,则;
③若,则.
其中正确结论的序号是________
(13)盒子中有4个白球和3个红球,现从盒子中依次不放回地抽取2个球,那么在第一次抽出白球的条件下,第二次抽出红球的概率是________
(14)某年级举办线上小型音乐会,由6个节目组成,演出顺序有如下要求:节目甲必须排在前两位,节目丙必须排在节目乙的下一个,则该小型音乐会节目演出顺序的编排方案共有________种. (用数字作答)
(15)已知函数,若f(m)=g(n)成立,则n-m的最小值为________
三、解答题共5小题,共40分。解答应写出文字说明,演算步骤或证明过程。
(16) (本小题8分)
已知函数
(Ⅰ)求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求f(x)的单调区间.
(17) (本小题8分)
为了迎接冬奥会,某中学推广冰上运动,从全校学生中随机抽取了100人,统计是否爱好冰上运动,得到如下的列表:
参考附表:
参考公式:,其中n=a+b+c+d
(I) 补全2x2 联表;
(Ⅱ)能否在犯错误的概率不超过0.05的前提下认为“爱好冰上运动与性别有关"?请说明理由.
(18)(本小题8分)
2020年5月1日起,《北京市垃圾分类管理条例》正式实施,某社区随机对200种垃圾辨识度进行了随机调查,经分类整理得到下表:
辨识率是指:一类垃圾中辨识准确度高的数量与该类垃圾的种类数的比值.
(Ⅰ)从社区调查的200种垃圾中随机选取一种,求这种垃圾辨识度高的概率;
(Ⅱ)从可回收物中有放回的抽取三种垃圾,记X为其中辨识度高的垃圾种数,求X的分布列和数学期望.
(19) (本小题8分)
已知函数.
(Ⅰ)求f(x)的极值;
(Ⅱ)若函数在定义域内有三个零点,求实数a的取值范围.
(20)(本小题8分)
设集合,若X是的子集,把X中所有数的和称为X的“容量”(规定空集的容量为0),若 X的容量为奇(偶)数,则称X为的奇(偶)子集.
(Ⅰ)当n=3时,写出的所有奇子集;
(Ⅱ)求证:当n≥3时,的所有奇子集的容量之和等于所有偶子集的容量之和;
(Ⅲ)当n≥3时,求的所有奇子集的容量之和.
参考答案
一、选择题(共10小题,每小题4分,共40分)
(1)A (2)B (3)B (4)D (5)D
(6)C (7)C (8)B (9)A (10)C
二、填空题(共5小题,每小题4分,共20分)
(11) (12)①③ (13)
(14) (15)
注:(12)题给出的结论中,有多个符合题目要求。全部选对得4分,不选或错选得0分,其他得2分。
三、解答题(共5小题,共40分)
(16)(共8分)
解:由题意可知函数的定义域为.
(Ⅰ)因为,
所以, ………1分
. ………2分
因为, ………3分
所以曲线在点处的切线方程为.………4分
(Ⅱ) 的定义域为. ………5分
因为,
由,得,. ………6分
因为函数的定义域为,
当变化时,,的变化情况如下表:
| |||
| |||
单调递减 | 极小值 | 单调递增 |
………7分
所以,的单调递增区间为,
的单调递减区间为. ………8分
(17)(共8分)
解:(Ⅰ)
| 爱好 | 不爱好 | 共计 |
男生 | |||
女生 | |||
共计 |
共需要填6个空,对2个空 ……1分
对4个空 ………2分
全对 ………4分
(Ⅱ)由题可知,
,经过计算,,………7分
参照附表,所以在犯错误的概率不超过的前提下,
可以认为“爱好冰上运动与性别有关”. ………8分
(18)(共8分)
解:(Ⅰ)由题意可知,样本中垃圾种类一共种,
辨识度高的垃圾种数是:.………1分
所求概率为. ………3分
(Ⅱ)的可能取值为. ………4分
依题意可知,.
,
,
,
. ………6分
所以的分布列为
………7分
. ………………8分
(19)(共8分)
解:由题意可知函数的定义域为.
(Ⅰ)因为,
所以. ………1分
由,得,. ………2分
当变化时,,的变化情况如下表:
|
|
| |||
单调递增 |
| 单调递减 | 单调递增 |
………3分
因此,当时,有极大值,并且极大值为;
当时,有极小值,并且极小值为.
………4分(全对给1分)
(Ⅱ)因为,
所以.
所以为一个零点.
所以“函数在定义域内有三个零点”可以转化为
“方程有两个非零实根”. ………5分
令,则,
所以,当时,,在上单调递减;
当时,,在上单调递增.
当时,有最小值. ………6分
若方程有两个非零实根,则,即.
又,,恒成立,不存在零点,………7分
所以.
综上,.
所以当时,函数在定义域内有三个零点.
………8分
(20)(共8分)
(Ⅰ)解:当时,.
的所有奇子集为. ………3分(少写或写错扣1分)
(Ⅱ)证明:首先证明的奇子集与偶子集个数相等.
设奇数,对于的每个奇子集,
当时,取且.
当时,取,则为的偶子集.
反之,亦然.
所以,的奇子集与偶子集是一一对应的.
所以,的奇子集与偶子集个数相等.
对于,,含的的子集共有个, …4分
其中必有一半是奇子集,一半是偶子集,从而对于每个数,在奇子集的和与偶子集的和中,所占的个数是一样的.
所以的所有奇子集的容量的和与所有偶子集的容量的和相等. …6分
(Ⅲ)解:由于每个元素在奇子集中都出现次,故奇子集的容量和为
. ………8分
①








