

还剩18页未读,
继续阅读
【数学】黑龙江省哈尔滨师范大学附属中学2019-2020学年高二下学期期末考试(文)(解析版)
展开
黑龙江省哈尔滨师范大学附属中学2019-2020学年
高二下学期期末考试(文)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的)
1.复数(其中i是虚数单位)的实部是( )
A.1 B.﹣1 C.﹣2 D.0
2.已知函数f(x)=sinx,其导函数为,则=( )
A.﹣ B. C. D.﹣
3.独立性检验中,为了调查变量X与变量Y的关系,经过计算得到P(K2≥3.841)=0.01,表示的意义是( )
A.有99%的把握认为变量X与变量Y没有关系
B.有1%的把握认为变量X与变量Y有关系
C.有0.01%的把握认为变量X与变量Y有关系
D.有99%的把握认为变量X与变量Y有关系
4.曲线y=x3﹣x在点(1,0)处的切线方程为( )
A.2x﹣y=0 B.2x+y﹣2=0 C.2x+y+2=0 D.2x﹣y﹣2=0
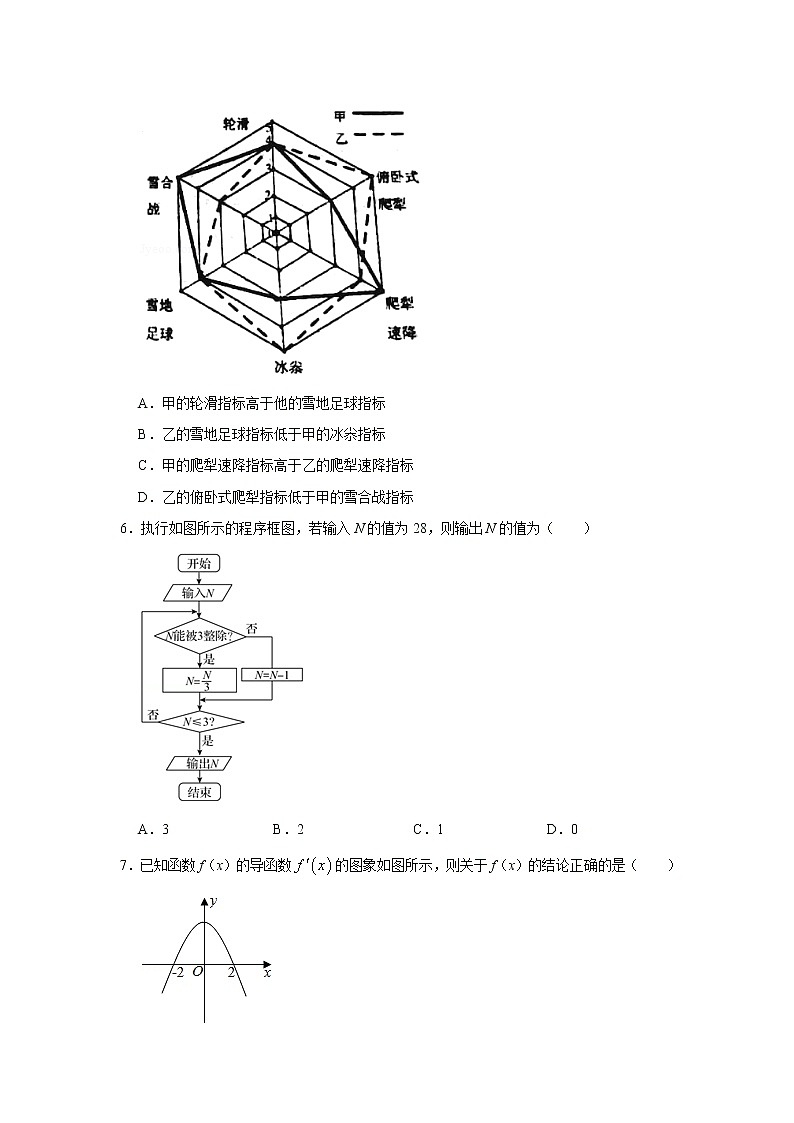
5.2020年冬奥会申办成功,让中国冰雪项目迎来了新的发展机会,“十四冬”作为北京冬奥会前重要的练兵场,对冰雪运动产生了不可忽视的带动作用.某校对冰雪体育社团中甲、乙两人的滑轮、雪合战、雪地足球、冰尜(ga)、爬犁速降及俯卧式爬犁6个冬季体育运动项目进行了指标测试(指标值满分为5分,分高者为优),根据测试情况绘制了如图所示的指标雷达图.则下面叙述正确的是( )
A.甲的轮滑指标高于他的雪地足球指标
B.乙的雪地足球指标低于甲的冰尜指标
C.甲的爬犁速降指标高于乙的爬犁速降指标
D.乙的俯卧式爬犁指标低于甲的雪合战指标
6.执行如图所示的程序框图,若输入N的值为28,则输出N的值为( )
A.3 B.2 C.1 D.0
7.已知函数f(x)的导函数的图象如图所示,则关于f(x)的结论正确的是( )
A.在区间(﹣2,2)上为减函数
B.在x=﹣2处取得极小值
C.在区间(﹣∞,﹣2),(2,+∞)上为增函数
D.在x=0处取得极大值
8.采用简单随机抽样的方法,从含有6个个体的总体中抽取1个容量为2的样本,则某个个体被抽到的概率为( )
A. B. C. D.
9.若某10人一次比赛得分数据如茎叶图所示,则这组数据的中位数是( )
A.82.5 B.83 C.93 D.72
10.若函数f(x)=kex﹣x2在区间(0,+∞)上单调递增,则实数k的取值范围是( )
A.[,+∞) B.(0,+∞) C.(,+∞) D.[0,+∞)
11.华罗庚是上世纪我国伟大的数学家,以华氏命名的数学科研成果有“华氏定理”、“华氏不等式”、“华王方法”等.他除了数学理论研究,还在生产一线大力推广了“优选法”和“统筹法”.“优选法”,是指研究如何用较少的试验次数,迅速找到最优方案的一种科学方法.在当前防疫取得重要进展的时刻,为防范机场带来的境外输入,某机场海关在对入境人员进行检测时采用了“优选法”提高检测效率:每16人为组,把每个人抽取的鼻咽拭子分泌物混合检查,如果为阴性则全部放行;若为阳性,则对该16人再次抽检确认感染者.
某组16人中恰有一人感染(鼻咽拭子样本检验将会是阳性),若逐一检测可能需要15次才能确认感染者.现在先把这16人均分为2组,选其中一组8人的样本混合检查,若为阴性则认定在另一组;若为阳性,则认定在本组.继续把认定的这组的8人均分两组,选其中一组4人的样本混合检查……以此类推,最终从这16人中认定那名感染者需要经过( )次检测.
A.3 B.4 C.6 D.7
12.已知函数f(x)=,函数g(x)=k(x﹣1),若方程f(x)=g(x)恰有三个实数解,则实数k的取值范围为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.总体由编号为01,02,…,29,30的30个个体组成,现从中抽取一个容量为6的样本,请以随机数表第1行第5列开始,向右读取,则选出来的第5个个体的编号为 .
70 29 17 12 13 40 33 12 38 26 13 89 51 03
56 62 18 37 35 96 83 50 87 75 97 12 55 93
14.一个社会调查机构就某地居民的月收入情况调查了1000人,并根据所得数据绘制了样本频率分布直方图(如图所示),则月收入在[2000,3500)范围内的人数为 .
15.若函数f(x)=x3﹣ax2+4在区间[0,2]上不单调,则实数a的取值范围为 .
16.用火柴棒按如图的方法搭三角形:
按图示的规律搭下去,则第100个图形所用火柴棒数为__________
三.解答题(解答应写出文字说明,证明过程或演算步骤)
17. (本小题满分10分) 在直角坐标系xOy中,以原点为极点,x轴非负半轴为极轴,已知直线的极坐标方程为l:ρcosθ+2ρsinθ=5,曲线C:=1.
(1)写出直线l的直角坐标方程和曲线C的参数方程;
(2)在曲线C上求一点P,使它到直线l的距离最小,并求出最小值.
18.(本小题满分12分) 设函数f(x)=2x3+3x2+ax+b,曲线y=f(x)在点(0,f(0))处的切线方程为y=﹣12x+1.
(1)求f(x)的解析式;
(2)求f(x)的极值.
19. (本小题满分12分) 已知f(x)=|x|+|x﹣2|.
(1)求不等式的解集;
(2)若f(x)的最小值为M,且a+2b+2c=M(a,b,c∈R),求证:.
20. (本小题满分12分)目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.
(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长潜伏者”的人数;
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取300人,得到如表表格.
(i)请将表格补充完整;
短潜伏者
长潜伏者
合计
60岁及以上
90
60岁以下
140
合计
300
(ii)研究发现,某药物对新冠病毒有一定的抑制作用,现需在样本中60岁以下的140名患者中按分层抽样方法抽取7人做I期临床试验,再从选取的7人中随机抽取两人做Ⅱ期临床试验,求两人中恰有1人为“长潜伏者”的概率.
21. (本小题满分12分)已知椭圆与过其右焦点F(1,0)的直线交于不同的两点A,B,线段AB的中点为
D,且直线l与直线OD的斜率之积为.
(1)求C的方程;
(2)设椭圆的左顶点为M,kMA,kMB如分别表示直线MA,MB的斜率,求证.
22. (本小题满分12分)设函数f(x)=x2+cos2x.
(Ⅰ)讨论函数f(x)的单调性.
(Ⅱ)若x≥0,不等式f(x)≥kx+1恒成立,求实数k的取值范围.
参考答案
一.选择题
1.复数(其中i是虚数单位)的实部是( )
A.1 B.﹣1 C.﹣2 D.0
【解答】解:∵=,
∴的实部是0.
故选:D.
2.已知函数f(x)=sinx,其导函数为f'(x),则f'()=( )
A.﹣ B. C. D.﹣
【解答】解:∵f(x)=sinx,
∴f′(x)=cosx,
∴.
故选:C.
3.独立性检验中,为了调查变量X与变量Y的关系,经过计算得到P(K2≥3.841)=0.01,表示的意义是( )
A.有99%的把握认为变量X与变量Y没有关系
B.有1%的把握认为变量X与变量Y有关系
C.有0.01%的把握认为变量X与变量Y有关系
D.有99%的把握认为变量X与变量Y有关系
【解答】解:独立性检验中,P(K2≥3.841)=0.01表示的意义是
有99%的把握认为变量X与变量Y有关系.
故选:D.
4.曲线y=x3﹣x在点(1,0)处的切线方程为( )
A.2x﹣y=0 B.2x+y﹣2=0 C.2x+y+2=0 D.2x﹣y﹣2=0
【解答】解:y=x3﹣x
∴y′=3x2﹣1,
所以k=3×12﹣1=2,
所以切线方程为y=2(x﹣1),
即2x﹣y﹣2=0
故选:D.
5.2020年冬奥会申办成功,让中国冰雪项目迎来了新的发展机会,“十四冬”作为北京冬奥会前重要的练兵场,对冰雪运动产生了不可忽视的带动作用.某校对冰雪体育社团中甲、乙两人的滑轮、雪合战、雪地足球、冰尜(ga)、爬犁速降及俯卧式爬犁6个冬季体育运动项目进行了指标测试(指标值满分为5分,分高者为优),根据测试情况绘制了如图所示的指标雷达图.则下面叙述正确的是( )
A.甲的轮滑指标高于他的雪地足球指标
B.乙的雪地足球指标低于甲的冰尜指标
C.甲的爬犁速降指标高于乙的爬犁速降指标
D.乙的俯卧式爬犁指标低于甲的雪合战指标
【解答】解:A选项,甲的滑轮指标为4分,雪地足球指标也为4分,故A错误;
B选项,甲的雪地足球指标为4分,乙的雪地足球指标也为4分,故B错误;
C选项,甲的爬犁速降指标为4分,乙的爬犁速降指标为4分,故C正确,
D选项,乙的俯卧式爬犁指标为5分,甲的雪合战指标为5分,故D错误.
故选:C.
6.执行如图所示的程序框图,若输入N的值为28,则输出N的值为( )
A.3 B.2 C.1 D.0
【解答】解:模拟程序的运行,可得
N=28,不能被3整除,可得:N=28﹣1=27;
27能被3整除,;
9能被3整除,,
此时,3≤3,终止循环,输出N=3.
故选:A.
7.已知函数f(x)的导函数f'(x)的图象如图所示,则关于f(x)的结论正确的是( )
A.在区间(﹣2,2)上为减函数
B.在x=﹣2处取得极小值
C.在区间(﹣∞,﹣2),(2,+∞)上为增函数
D.在x=0处取得极大值
【解答】解:由图象得:f(x)在(﹣∞,﹣2)递减,在(﹣2,2)递增,在(2,+∞)递减,
故f(x)在x=﹣2取极小值,在x=2取极大值,
故选:B.
8.采用简单随机抽样的方法,从含有6个个体的总体中抽取1个容量为2的样本,则某个个体被抽到的概率为( )
A. B. C. D.
【解答】解:由题意事件“抽取一个容量为2的样本,某个被抽到”包含了5个基本事件,而总的基本事件数是C62=15
∴事件“某个个体被抽到的”概率是=
故选:B.
9.若某10人一次比赛得分数据如茎叶图所示,则这组数据的中位数是( )
A.82.5 B.83 C.93 D.72
【解答】解:将这组数据从小到大排列为72,74,76,81,82,83,86,93,93,99,
则这组数据的中位数是=82.5.
故选:A.
10.若函数f(x)=kex﹣x2在区间(0,+∞)上单调递增,则实数k的取值范围是( )
A.[,+∞) B.(0,+∞) C.(,+∞) D.[0,+∞)
【解答】解:f′(x)=kex﹣x,依题意,kex﹣x≥0在(0,+∞)上恒成立,即在(0,+∞)上恒成立,
令,则,
易知函数g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴,
∴.
故选:A.
11.华罗庚是上世纪我国伟大的数学家,以华氏命名的数学科研成果有“华氏定理”、“华氏不等式”、“华王方法”等.他除了数学理论研究,还在生产一线大力推广了“优选法”和“统筹法”.“优选法”,是指研究如何用较少的试验次数,迅速找到最优方案的一种科学方法.在当前防疫取得重要进展的时刻,为防范机场带来的境外输入,某机场海关在对入境人员进行检测时采用了“优选法”提高检测效率:每16人为组,把每个人抽取的鼻咽拭子分泌物混合检查,如果为阴性则全部放行;若为阳性,则对该16人再次抽检确认感染者.
某组16人中恰有一人感染(鼻咽拭子样本检验将会是阳性),若逐一检测可能需要15次才能确认感染者.现在先把这16人均分为2组,选其中一组8人的样本混合检查,若为阴性则认定在另一组;若为阳性,则认定在本组.继续把认定的这组的8人均分两组,选其中一组4人的样本混合检查……以此类推,最终从这16人中认定那名感染者需要经过( )次检测.
A.3 B.4 C.6 D.7
【解答】解:第一次:16人分两组,每组8人,如果第一组检测结果为阳性,放行第二组,留下第一组继续检测,
如果第一组检测结果为阴性,放行第一组,留下第二组继续检测;
第二次:留下的8人分两组,每组4人,如果第一组检测结果为阳性,放行第二组,留下第一组继续检测,
如果第一组检测结果为阴性,放行第一组,留下第二组继续检测;
第三次:留下的4人分两组,每组2人,如果第一组检测结果为阳性,放行第二组,留下第一组继续检测,
如果第一组检测结果为阴性,放行第一组,留下第二组继续检测;
第四次:留下的2人分两组,每组1人,如果第一人检测结果为阳性,则第2人没有感染.
如果第一组检测结果为阴性,则第2人感染.
综上,最终从这16人中认定那名感染者需要经过4次检测.
故选:B.
12.已知函数f(x)=,函数g(x)=k(x﹣1),若方程f(x)=g(x)恰有三个实数解,则实数k的取值范围为( )
A. B. C. D.
【解答】解:依题意,画出的图象,
如图.直线g(x)=k(x﹣1)过定点(1,0),
由图象可知,函数g(x)的图象与的图象相切时,
函数f(x),g(x)的图象恰有两个交点.
下面利用导数法求该切线的斜率.
设切点为P(x0,y0),由f'(x)=x+2,x<0,
得,化简得,
解得或(舍去),
要使方程f(x)=g(x)恰有三个实数解,
则函数f(x),g(x)的图象恰有三个交点,
结合图象可知,
所以实数k的取值范围为,
故选:D.
二.填空题
13.总体由编号为01,02,…,29,30的30个个体组成,现从中抽取一个容量为6的样本,请以随机数表第1行第5列开始,向右读取,则选出来的第5个个体的编号为( )
70 29 17 12 13 40 33 12 38 26 13 89 51 03
56 62 18 37 35 96 83 50 87 75 97 12 55 93
A.12 B.13 C.03 D.40
【解答】解:从随机数表第1行第5列开始,向右读取,
依次选取两个数字中小于30的编号依次为17,12,13,26,03
则第5个个体的编号为03.
14.一个社会调查机构就某地居民的月收入情况调查了1000人,并根据所得数据绘制了样本频率分布直方图(如图所示),则月收入在[2000,3500)范围内的人数为 700 .
【解答】解:由图[2000,3500)收入段的频率是(0.0005+0.0005+0.0004)×500=0.7;
则在[2000,3500)收入段应抽出人数为0.7×1000=700.
故答案为:700.
15.若函数f(x)=x3﹣ax2+4在区间[0,2]上不单调,则实数a的取值范围为 (0,3) .
【解答】解:f′(x)=3x2﹣2ax,
∵函数f(x)=x3﹣ax2+4在区间[0,2]上不单调,
∴3x2﹣2ax=0在(0,2)内有解.
∴a=x∈(0,3).
故答案为:(0,3).
16.用火柴棒按如图的方法搭三角形:
按图示的规律搭下去,则第100个图形所用火柴棒数为____201______
A.401 B.201 C.402 D.202
【解答】解:由图形可知,第一个图形用3个火柴,以后每一个比前一个多两个火柴,
则第n个使用火柴为2n+1,则第100个图形所用火柴棒数为2×100+1=201.
三.解答题
17. 在直角坐标系xOy中,以原点为极点,x轴非负半轴为极轴,已知直线的极坐标方程为l:ρcosθ+2ρsinθ=5,曲线C:=1.
(1)写出直线l的直角坐标方程和曲线C的参数方程;
(2)在曲线C上求一点P,使它到直线l的距离最小,并求出最小值.
【解答】解:(1)直线的极坐标方程为l:ρcosθ+2ρsinθ=5,转换为直角坐标方程为:x+2y﹣5=0.
曲线C:=1.转换为参数方程为(θ为参数).
(2)设,
则,
当,
即,(k∈Z),
此时,
即时,.
18.设函数f(x)=2x3+3x2+ax+b,曲线y=f(x)在点(0,f(0))处的切线方程为y=﹣12x+1.
(1)求f(x)的解析式;
(2)求f(x)的极值.
【解答】解:(1)f′(x)=6x2+6x+a,
k切=f′(0)=a,
又因为切线方程为y=﹣12x+1,
所以k切=﹣12,
得a=﹣12,
因为切点在切线上也在曲线上,
所以,
所以b=1,
所以f(x)的解析式为y=2x3+3x2﹣12x+1.
(2)f(x)定义域为R,
f′(x)=6x2+6x﹣12
令f′(x)=0得,x=﹣2或1,
所以在(﹣∞,﹣2),(1,+∞)上单调递增,
在(﹣2,1)上单调递减,
所以f(x)极大值=f(﹣2)=21
f(x)极小值=f(1)=﹣6.
19.已知f(x)=|x|+|x﹣2|.
(1)求不等式的解集;
(2)若f(x)的最小值为M,且a+2b+2c=M(a,b,c∈R),求证:.
【解答】(1)解:∵f(x)=|x|+|x﹣2|,
∴当x<0时,等价于|x|+|x﹣2|>﹣4,该不等式恒成立;
当0<x≤2时,等价于2>4,该不等式不成立;
当x>2时,等价于,解得x>3,
∴不等式的解集为(﹣∞,0)∪(3,+∞).
(2)证明:∵f(x)=|x|+|x﹣2|≥|x﹣(x﹣2)|=2,
当且仅当0≤x≤2时取等号,∴M=2,a+2b+2c=2,
由柯西不等式,可得4=(a+2b+2c)2≤(12+22+22)(a2+b2+c2)=9(a2+b2+c2),
当且仅当时等号成立,
∴.
时,函数f(x)为,当x=4时,函数f(x)的最小值为.
20. 目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.
(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长潜伏者”的人数;
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取300人,得到如表表格.
(i)请将表格补充完整;
短潜伏者
长潜伏者
合计
60岁及以上
90
60岁以下
140
合计
300
(ii)研究发现,某药物对新冠病毒有一定的抑制作用,现需在样本中60岁以下的140名患者中按分层抽样方法抽取7人做I期临床试验,再从选取的7人中随机抽取两人做Ⅱ期临床试验,求两人中恰有1人为“长潜伏者”的概率.
【解答】解:(1)平均数x=(0.02×1+0.08×3+0.15×5+0.18×7+0.03×9+0.03×11+0.01×13)×2=6,
“长潜伏者”即潜伏期时间不低于6天的频率为0.5,
所以500人中“长潜伏者”的人数为500×0.5=250人;
(2)(i)由题意补充后的表格如图:
短潜伏者
长潜伏者
合计
60岁及以上
90
70
160
60岁以下
60
80
140
合计
150
150
300
(ii)由分层抽样知7人中,“短潜伏者”有3人,记为a,b,c,“长潜伏者”有4人,记为D,E,F,G,
从中抽取2人,共有21种不同结果,分别为:
(a,b),(a,c),(a,D),(a,E),(a,F),(a,G),(b,c),(b,D),(b,E),(b,F),(b,G),
(c,D),(c,E),(c,F),(c,G),(D,E),(D,F),(D,G),(E,F),(E,G),(F,G),
两人中恰好有1人为“长潜伏者”包含了12种结果.
所以两人中恰有1人为“长潜伏者”的概率为.
21. 已知椭圆与过其右焦点F(1,0)的直线交于不同的两点A,B,线段AB的中点为
D,且直线l与直线OD的斜率之积为.
(1)求C的方程;
(2)设椭圆的左顶点为M,kMA,kMB如分别表示直线MA,MB的斜率,求证.
【解答】解:(1)设A(x1,y1),B(x2,y2),D(x0,y0),
将点A,B坐标代入椭圆的方程两式相减+=0,
所以kAB==﹣,
因为D为AB的中点,所以kOD=,
所以kAB•kOD=﹣=﹣,
所以=,又a2﹣b2=1,解得:a2=4,b2=3,
所以椭圆C的方程为:+=1;
(2)由(1)可得左顶点M(﹣2,0),由题意设直线AB的方程:x=my+1,
联立直线与椭圆的方程:整理可得:(4+3m2)y2+6my﹣9=0,
所以y1+y2=﹣,y1y2=﹣,
所以kAM+kBM=+==
==﹣m,
因为kAB•kOD=﹣•kOD=﹣,所以m=﹣kOD,
所以kAM+kBM=kOD.
22. 设函数f(x)=x2+cos2x.
(Ⅰ)讨论函数f(x)的单调性.
(Ⅱ)若x≥0,不等式f(x)≥kx+1恒成立,求实数k的取值范围.
【解答】解:(Ⅰ)f′(x)=2x﹣2sinxcosx=2x﹣sin2x,f''(x)=2﹣2cos2x=2(1﹣cos2x)≥0,
∴函数f′(x)为增函数,又f′(0)=0,
∴当x<0时,f′(x)<0,当x>0时,f′(x)>0,
∴函数f(x)在(﹣∞,0)上单调递减,在(0,+∞)上单调递增;
(Ⅱ)不等式f(x)≥kx+1即为x2﹣kx﹣1+cos2x≥0,设g(x)=x2﹣kx﹣1+cos2x,x≥0,
则g′(x)=2x﹣k﹣sin2x,
由(Ⅰ)可知,g′(x)是[0,+∞)上的增函数,
因为g′(0)=﹣k,
所以当k≤0时,g′(0)≥0,函数g(x)在区间[0,+∞)上单调递增,g(x)≥g(0)=0,符合题意;
当k>0时,g′(0)=﹣k<0,故存在x0>0,使得g′(x0)=0,
且当x∈(0,x0)时,g′(x)<0,当x∈(x0,+∞)时,g′(x)>0,
所以函数g(x)在x∈(0,x0)上为减函数,在x∈(x0,+∞)上为增函数,故g(x)min=g(x0)<g(0)=0,不合题意.
综上,实数k的取值范围为(﹣∞,0].
高二下学期期末考试(文)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的)
1.复数(其中i是虚数单位)的实部是( )
A.1 B.﹣1 C.﹣2 D.0
2.已知函数f(x)=sinx,其导函数为,则=( )
A.﹣ B. C. D.﹣
3.独立性检验中,为了调查变量X与变量Y的关系,经过计算得到P(K2≥3.841)=0.01,表示的意义是( )
A.有99%的把握认为变量X与变量Y没有关系
B.有1%的把握认为变量X与变量Y有关系
C.有0.01%的把握认为变量X与变量Y有关系
D.有99%的把握认为变量X与变量Y有关系
4.曲线y=x3﹣x在点(1,0)处的切线方程为( )
A.2x﹣y=0 B.2x+y﹣2=0 C.2x+y+2=0 D.2x﹣y﹣2=0
5.2020年冬奥会申办成功,让中国冰雪项目迎来了新的发展机会,“十四冬”作为北京冬奥会前重要的练兵场,对冰雪运动产生了不可忽视的带动作用.某校对冰雪体育社团中甲、乙两人的滑轮、雪合战、雪地足球、冰尜(ga)、爬犁速降及俯卧式爬犁6个冬季体育运动项目进行了指标测试(指标值满分为5分,分高者为优),根据测试情况绘制了如图所示的指标雷达图.则下面叙述正确的是( )
A.甲的轮滑指标高于他的雪地足球指标
B.乙的雪地足球指标低于甲的冰尜指标
C.甲的爬犁速降指标高于乙的爬犁速降指标
D.乙的俯卧式爬犁指标低于甲的雪合战指标
6.执行如图所示的程序框图,若输入N的值为28,则输出N的值为( )
A.3 B.2 C.1 D.0
7.已知函数f(x)的导函数的图象如图所示,则关于f(x)的结论正确的是( )
A.在区间(﹣2,2)上为减函数
B.在x=﹣2处取得极小值
C.在区间(﹣∞,﹣2),(2,+∞)上为增函数
D.在x=0处取得极大值
8.采用简单随机抽样的方法,从含有6个个体的总体中抽取1个容量为2的样本,则某个个体被抽到的概率为( )
A. B. C. D.
9.若某10人一次比赛得分数据如茎叶图所示,则这组数据的中位数是( )
A.82.5 B.83 C.93 D.72
10.若函数f(x)=kex﹣x2在区间(0,+∞)上单调递增,则实数k的取值范围是( )
A.[,+∞) B.(0,+∞) C.(,+∞) D.[0,+∞)
11.华罗庚是上世纪我国伟大的数学家,以华氏命名的数学科研成果有“华氏定理”、“华氏不等式”、“华王方法”等.他除了数学理论研究,还在生产一线大力推广了“优选法”和“统筹法”.“优选法”,是指研究如何用较少的试验次数,迅速找到最优方案的一种科学方法.在当前防疫取得重要进展的时刻,为防范机场带来的境外输入,某机场海关在对入境人员进行检测时采用了“优选法”提高检测效率:每16人为组,把每个人抽取的鼻咽拭子分泌物混合检查,如果为阴性则全部放行;若为阳性,则对该16人再次抽检确认感染者.
某组16人中恰有一人感染(鼻咽拭子样本检验将会是阳性),若逐一检测可能需要15次才能确认感染者.现在先把这16人均分为2组,选其中一组8人的样本混合检查,若为阴性则认定在另一组;若为阳性,则认定在本组.继续把认定的这组的8人均分两组,选其中一组4人的样本混合检查……以此类推,最终从这16人中认定那名感染者需要经过( )次检测.
A.3 B.4 C.6 D.7
12.已知函数f(x)=,函数g(x)=k(x﹣1),若方程f(x)=g(x)恰有三个实数解,则实数k的取值范围为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.总体由编号为01,02,…,29,30的30个个体组成,现从中抽取一个容量为6的样本,请以随机数表第1行第5列开始,向右读取,则选出来的第5个个体的编号为 .
70 29 17 12 13 40 33 12 38 26 13 89 51 03
56 62 18 37 35 96 83 50 87 75 97 12 55 93
14.一个社会调查机构就某地居民的月收入情况调查了1000人,并根据所得数据绘制了样本频率分布直方图(如图所示),则月收入在[2000,3500)范围内的人数为 .
15.若函数f(x)=x3﹣ax2+4在区间[0,2]上不单调,则实数a的取值范围为 .
16.用火柴棒按如图的方法搭三角形:
按图示的规律搭下去,则第100个图形所用火柴棒数为__________
三.解答题(解答应写出文字说明,证明过程或演算步骤)
17. (本小题满分10分) 在直角坐标系xOy中,以原点为极点,x轴非负半轴为极轴,已知直线的极坐标方程为l:ρcosθ+2ρsinθ=5,曲线C:=1.
(1)写出直线l的直角坐标方程和曲线C的参数方程;
(2)在曲线C上求一点P,使它到直线l的距离最小,并求出最小值.
18.(本小题满分12分) 设函数f(x)=2x3+3x2+ax+b,曲线y=f(x)在点(0,f(0))处的切线方程为y=﹣12x+1.
(1)求f(x)的解析式;
(2)求f(x)的极值.
19. (本小题满分12分) 已知f(x)=|x|+|x﹣2|.
(1)求不等式的解集;
(2)若f(x)的最小值为M,且a+2b+2c=M(a,b,c∈R),求证:.
20. (本小题满分12分)目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.
(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长潜伏者”的人数;
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取300人,得到如表表格.
(i)请将表格补充完整;
短潜伏者
长潜伏者
合计
60岁及以上
90
60岁以下
140
合计
300
(ii)研究发现,某药物对新冠病毒有一定的抑制作用,现需在样本中60岁以下的140名患者中按分层抽样方法抽取7人做I期临床试验,再从选取的7人中随机抽取两人做Ⅱ期临床试验,求两人中恰有1人为“长潜伏者”的概率.
21. (本小题满分12分)已知椭圆与过其右焦点F(1,0)的直线交于不同的两点A,B,线段AB的中点为
D,且直线l与直线OD的斜率之积为.
(1)求C的方程;
(2)设椭圆的左顶点为M,kMA,kMB如分别表示直线MA,MB的斜率,求证.
22. (本小题满分12分)设函数f(x)=x2+cos2x.
(Ⅰ)讨论函数f(x)的单调性.
(Ⅱ)若x≥0,不等式f(x)≥kx+1恒成立,求实数k的取值范围.
参考答案
一.选择题
1.复数(其中i是虚数单位)的实部是( )
A.1 B.﹣1 C.﹣2 D.0
【解答】解:∵=,
∴的实部是0.
故选:D.
2.已知函数f(x)=sinx,其导函数为f'(x),则f'()=( )
A.﹣ B. C. D.﹣
【解答】解:∵f(x)=sinx,
∴f′(x)=cosx,
∴.
故选:C.
3.独立性检验中,为了调查变量X与变量Y的关系,经过计算得到P(K2≥3.841)=0.01,表示的意义是( )
A.有99%的把握认为变量X与变量Y没有关系
B.有1%的把握认为变量X与变量Y有关系
C.有0.01%的把握认为变量X与变量Y有关系
D.有99%的把握认为变量X与变量Y有关系
【解答】解:独立性检验中,P(K2≥3.841)=0.01表示的意义是
有99%的把握认为变量X与变量Y有关系.
故选:D.
4.曲线y=x3﹣x在点(1,0)处的切线方程为( )
A.2x﹣y=0 B.2x+y﹣2=0 C.2x+y+2=0 D.2x﹣y﹣2=0
【解答】解:y=x3﹣x
∴y′=3x2﹣1,
所以k=3×12﹣1=2,
所以切线方程为y=2(x﹣1),
即2x﹣y﹣2=0
故选:D.
5.2020年冬奥会申办成功,让中国冰雪项目迎来了新的发展机会,“十四冬”作为北京冬奥会前重要的练兵场,对冰雪运动产生了不可忽视的带动作用.某校对冰雪体育社团中甲、乙两人的滑轮、雪合战、雪地足球、冰尜(ga)、爬犁速降及俯卧式爬犁6个冬季体育运动项目进行了指标测试(指标值满分为5分,分高者为优),根据测试情况绘制了如图所示的指标雷达图.则下面叙述正确的是( )
A.甲的轮滑指标高于他的雪地足球指标
B.乙的雪地足球指标低于甲的冰尜指标
C.甲的爬犁速降指标高于乙的爬犁速降指标
D.乙的俯卧式爬犁指标低于甲的雪合战指标
【解答】解:A选项,甲的滑轮指标为4分,雪地足球指标也为4分,故A错误;
B选项,甲的雪地足球指标为4分,乙的雪地足球指标也为4分,故B错误;
C选项,甲的爬犁速降指标为4分,乙的爬犁速降指标为4分,故C正确,
D选项,乙的俯卧式爬犁指标为5分,甲的雪合战指标为5分,故D错误.
故选:C.
6.执行如图所示的程序框图,若输入N的值为28,则输出N的值为( )
A.3 B.2 C.1 D.0
【解答】解:模拟程序的运行,可得
N=28,不能被3整除,可得:N=28﹣1=27;
27能被3整除,;
9能被3整除,,
此时,3≤3,终止循环,输出N=3.
故选:A.
7.已知函数f(x)的导函数f'(x)的图象如图所示,则关于f(x)的结论正确的是( )
A.在区间(﹣2,2)上为减函数
B.在x=﹣2处取得极小值
C.在区间(﹣∞,﹣2),(2,+∞)上为增函数
D.在x=0处取得极大值
【解答】解:由图象得:f(x)在(﹣∞,﹣2)递减,在(﹣2,2)递增,在(2,+∞)递减,
故f(x)在x=﹣2取极小值,在x=2取极大值,
故选:B.
8.采用简单随机抽样的方法,从含有6个个体的总体中抽取1个容量为2的样本,则某个个体被抽到的概率为( )
A. B. C. D.
【解答】解:由题意事件“抽取一个容量为2的样本,某个被抽到”包含了5个基本事件,而总的基本事件数是C62=15
∴事件“某个个体被抽到的”概率是=
故选:B.
9.若某10人一次比赛得分数据如茎叶图所示,则这组数据的中位数是( )
A.82.5 B.83 C.93 D.72
【解答】解:将这组数据从小到大排列为72,74,76,81,82,83,86,93,93,99,
则这组数据的中位数是=82.5.
故选:A.
10.若函数f(x)=kex﹣x2在区间(0,+∞)上单调递增,则实数k的取值范围是( )
A.[,+∞) B.(0,+∞) C.(,+∞) D.[0,+∞)
【解答】解:f′(x)=kex﹣x,依题意,kex﹣x≥0在(0,+∞)上恒成立,即在(0,+∞)上恒成立,
令,则,
易知函数g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴,
∴.
故选:A.
11.华罗庚是上世纪我国伟大的数学家,以华氏命名的数学科研成果有“华氏定理”、“华氏不等式”、“华王方法”等.他除了数学理论研究,还在生产一线大力推广了“优选法”和“统筹法”.“优选法”,是指研究如何用较少的试验次数,迅速找到最优方案的一种科学方法.在当前防疫取得重要进展的时刻,为防范机场带来的境外输入,某机场海关在对入境人员进行检测时采用了“优选法”提高检测效率:每16人为组,把每个人抽取的鼻咽拭子分泌物混合检查,如果为阴性则全部放行;若为阳性,则对该16人再次抽检确认感染者.
某组16人中恰有一人感染(鼻咽拭子样本检验将会是阳性),若逐一检测可能需要15次才能确认感染者.现在先把这16人均分为2组,选其中一组8人的样本混合检查,若为阴性则认定在另一组;若为阳性,则认定在本组.继续把认定的这组的8人均分两组,选其中一组4人的样本混合检查……以此类推,最终从这16人中认定那名感染者需要经过( )次检测.
A.3 B.4 C.6 D.7
【解答】解:第一次:16人分两组,每组8人,如果第一组检测结果为阳性,放行第二组,留下第一组继续检测,
如果第一组检测结果为阴性,放行第一组,留下第二组继续检测;
第二次:留下的8人分两组,每组4人,如果第一组检测结果为阳性,放行第二组,留下第一组继续检测,
如果第一组检测结果为阴性,放行第一组,留下第二组继续检测;
第三次:留下的4人分两组,每组2人,如果第一组检测结果为阳性,放行第二组,留下第一组继续检测,
如果第一组检测结果为阴性,放行第一组,留下第二组继续检测;
第四次:留下的2人分两组,每组1人,如果第一人检测结果为阳性,则第2人没有感染.
如果第一组检测结果为阴性,则第2人感染.
综上,最终从这16人中认定那名感染者需要经过4次检测.
故选:B.
12.已知函数f(x)=,函数g(x)=k(x﹣1),若方程f(x)=g(x)恰有三个实数解,则实数k的取值范围为( )
A. B. C. D.
【解答】解:依题意,画出的图象,
如图.直线g(x)=k(x﹣1)过定点(1,0),
由图象可知,函数g(x)的图象与的图象相切时,
函数f(x),g(x)的图象恰有两个交点.
下面利用导数法求该切线的斜率.
设切点为P(x0,y0),由f'(x)=x+2,x<0,
得,化简得,
解得或(舍去),
要使方程f(x)=g(x)恰有三个实数解,
则函数f(x),g(x)的图象恰有三个交点,
结合图象可知,
所以实数k的取值范围为,
故选:D.
二.填空题
13.总体由编号为01,02,…,29,30的30个个体组成,现从中抽取一个容量为6的样本,请以随机数表第1行第5列开始,向右读取,则选出来的第5个个体的编号为( )
70 29 17 12 13 40 33 12 38 26 13 89 51 03
56 62 18 37 35 96 83 50 87 75 97 12 55 93
A.12 B.13 C.03 D.40
【解答】解:从随机数表第1行第5列开始,向右读取,
依次选取两个数字中小于30的编号依次为17,12,13,26,03
则第5个个体的编号为03.
14.一个社会调查机构就某地居民的月收入情况调查了1000人,并根据所得数据绘制了样本频率分布直方图(如图所示),则月收入在[2000,3500)范围内的人数为 700 .
【解答】解:由图[2000,3500)收入段的频率是(0.0005+0.0005+0.0004)×500=0.7;
则在[2000,3500)收入段应抽出人数为0.7×1000=700.
故答案为:700.
15.若函数f(x)=x3﹣ax2+4在区间[0,2]上不单调,则实数a的取值范围为 (0,3) .
【解答】解:f′(x)=3x2﹣2ax,
∵函数f(x)=x3﹣ax2+4在区间[0,2]上不单调,
∴3x2﹣2ax=0在(0,2)内有解.
∴a=x∈(0,3).
故答案为:(0,3).
16.用火柴棒按如图的方法搭三角形:
按图示的规律搭下去,则第100个图形所用火柴棒数为____201______
A.401 B.201 C.402 D.202
【解答】解:由图形可知,第一个图形用3个火柴,以后每一个比前一个多两个火柴,
则第n个使用火柴为2n+1,则第100个图形所用火柴棒数为2×100+1=201.
三.解答题
17. 在直角坐标系xOy中,以原点为极点,x轴非负半轴为极轴,已知直线的极坐标方程为l:ρcosθ+2ρsinθ=5,曲线C:=1.
(1)写出直线l的直角坐标方程和曲线C的参数方程;
(2)在曲线C上求一点P,使它到直线l的距离最小,并求出最小值.
【解答】解:(1)直线的极坐标方程为l:ρcosθ+2ρsinθ=5,转换为直角坐标方程为:x+2y﹣5=0.
曲线C:=1.转换为参数方程为(θ为参数).
(2)设,
则,
当,
即,(k∈Z),
此时,
即时,.
18.设函数f(x)=2x3+3x2+ax+b,曲线y=f(x)在点(0,f(0))处的切线方程为y=﹣12x+1.
(1)求f(x)的解析式;
(2)求f(x)的极值.
【解答】解:(1)f′(x)=6x2+6x+a,
k切=f′(0)=a,
又因为切线方程为y=﹣12x+1,
所以k切=﹣12,
得a=﹣12,
因为切点在切线上也在曲线上,
所以,
所以b=1,
所以f(x)的解析式为y=2x3+3x2﹣12x+1.
(2)f(x)定义域为R,
f′(x)=6x2+6x﹣12
令f′(x)=0得,x=﹣2或1,
所以在(﹣∞,﹣2),(1,+∞)上单调递增,
在(﹣2,1)上单调递减,
所以f(x)极大值=f(﹣2)=21
f(x)极小值=f(1)=﹣6.
19.已知f(x)=|x|+|x﹣2|.
(1)求不等式的解集;
(2)若f(x)的最小值为M,且a+2b+2c=M(a,b,c∈R),求证:.
【解答】(1)解:∵f(x)=|x|+|x﹣2|,
∴当x<0时,等价于|x|+|x﹣2|>﹣4,该不等式恒成立;
当0<x≤2时,等价于2>4,该不等式不成立;
当x>2时,等价于,解得x>3,
∴不等式的解集为(﹣∞,0)∪(3,+∞).
(2)证明:∵f(x)=|x|+|x﹣2|≥|x﹣(x﹣2)|=2,
当且仅当0≤x≤2时取等号,∴M=2,a+2b+2c=2,
由柯西不等式,可得4=(a+2b+2c)2≤(12+22+22)(a2+b2+c2)=9(a2+b2+c2),
当且仅当时等号成立,
∴.
时,函数f(x)为,当x=4时,函数f(x)的最小值为.
20. 目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.
(1)求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长潜伏者”的人数;
(2)为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取300人,得到如表表格.
(i)请将表格补充完整;
短潜伏者
长潜伏者
合计
60岁及以上
90
60岁以下
140
合计
300
(ii)研究发现,某药物对新冠病毒有一定的抑制作用,现需在样本中60岁以下的140名患者中按分层抽样方法抽取7人做I期临床试验,再从选取的7人中随机抽取两人做Ⅱ期临床试验,求两人中恰有1人为“长潜伏者”的概率.
【解答】解:(1)平均数x=(0.02×1+0.08×3+0.15×5+0.18×7+0.03×9+0.03×11+0.01×13)×2=6,
“长潜伏者”即潜伏期时间不低于6天的频率为0.5,
所以500人中“长潜伏者”的人数为500×0.5=250人;
(2)(i)由题意补充后的表格如图:
短潜伏者
长潜伏者
合计
60岁及以上
90
70
160
60岁以下
60
80
140
合计
150
150
300
(ii)由分层抽样知7人中,“短潜伏者”有3人,记为a,b,c,“长潜伏者”有4人,记为D,E,F,G,
从中抽取2人,共有21种不同结果,分别为:
(a,b),(a,c),(a,D),(a,E),(a,F),(a,G),(b,c),(b,D),(b,E),(b,F),(b,G),
(c,D),(c,E),(c,F),(c,G),(D,E),(D,F),(D,G),(E,F),(E,G),(F,G),
两人中恰好有1人为“长潜伏者”包含了12种结果.
所以两人中恰有1人为“长潜伏者”的概率为.
21. 已知椭圆与过其右焦点F(1,0)的直线交于不同的两点A,B,线段AB的中点为
D,且直线l与直线OD的斜率之积为.
(1)求C的方程;
(2)设椭圆的左顶点为M,kMA,kMB如分别表示直线MA,MB的斜率,求证.
【解答】解:(1)设A(x1,y1),B(x2,y2),D(x0,y0),
将点A,B坐标代入椭圆的方程两式相减+=0,
所以kAB==﹣,
因为D为AB的中点,所以kOD=,
所以kAB•kOD=﹣=﹣,
所以=,又a2﹣b2=1,解得:a2=4,b2=3,
所以椭圆C的方程为:+=1;
(2)由(1)可得左顶点M(﹣2,0),由题意设直线AB的方程:x=my+1,
联立直线与椭圆的方程:整理可得:(4+3m2)y2+6my﹣9=0,
所以y1+y2=﹣,y1y2=﹣,
所以kAM+kBM=+==
==﹣m,
因为kAB•kOD=﹣•kOD=﹣,所以m=﹣kOD,
所以kAM+kBM=kOD.
22. 设函数f(x)=x2+cos2x.
(Ⅰ)讨论函数f(x)的单调性.
(Ⅱ)若x≥0,不等式f(x)≥kx+1恒成立,求实数k的取值范围.
【解答】解:(Ⅰ)f′(x)=2x﹣2sinxcosx=2x﹣sin2x,f''(x)=2﹣2cos2x=2(1﹣cos2x)≥0,
∴函数f′(x)为增函数,又f′(0)=0,
∴当x<0时,f′(x)<0,当x>0时,f′(x)>0,
∴函数f(x)在(﹣∞,0)上单调递减,在(0,+∞)上单调递增;
(Ⅱ)不等式f(x)≥kx+1即为x2﹣kx﹣1+cos2x≥0,设g(x)=x2﹣kx﹣1+cos2x,x≥0,
则g′(x)=2x﹣k﹣sin2x,
由(Ⅰ)可知,g′(x)是[0,+∞)上的增函数,
因为g′(0)=﹣k,
所以当k≤0时,g′(0)≥0,函数g(x)在区间[0,+∞)上单调递增,g(x)≥g(0)=0,符合题意;
当k>0时,g′(0)=﹣k<0,故存在x0>0,使得g′(x0)=0,
且当x∈(0,x0)时,g′(x)<0,当x∈(x0,+∞)时,g′(x)>0,
所以函数g(x)在x∈(0,x0)上为减函数,在x∈(x0,+∞)上为增函数,故g(x)min=g(x0)<g(0)=0,不合题意.
综上,实数k的取值范围为(﹣∞,0].
相关资料
更多








