备战2021年中考训练 专题十 四边形


专题十 四边形
一、单选题
1.（2020·台州）把一张宽为1cm的长方形纸片ABCD折叠成如图所示的阴影图案，顶点A，D互相重合，中间空白部分是以E为直角顶点，腰长为2cm的等腰直角三角形，则纸片的长AD（单位:cm）为（   ）

A. 7+3                              B. 7+4                              C. 8+3                              D. 8+4
2.（2020·台州）下是关于某个四边形的三个结论:①它的对角线相等；②它是一个正方形;③它是一个矩形.下列推理过程正确的是（   ）
A. 由②推出③，由③推出①                                    B. 由①推出②，由②推出③
C. 由③推出①，由①推出②                                    D. 由①推出③，由③推出②
3.（2020·台州）如图，已知线段AB，分别以A，B为圆心，大于 AB同样长为半径画弧，两弧交于点C，D，连接AC，AD，BC，BD，CD，则下列说法错误的是（  ）

A. AB平分∠CAD                       B. CD平分∠ACB                       C. AB⊥CD                       D. AB=CD
4.（2020·温州）如图，在△ABC中，∠A=40°，AB=AC，点D在AC边上，以CB，CD为边作 BCDE，则∠E的度数为(    )

A. 40°                                       B. 50°                                       C. 60°                                       D. 70°
5.（2020·湖州）四边形具有不稳定性，对于四条边长确定的四边形，当内角度数发生变化时，其形状也会随之改变，如图，改变正方形ABCD的内角，正方形ABCD变为菱形ABC′D′，若∠D′AB＝30°，则菱形ABC′D′的面积与正方形ABCD的面积之比是（   ）

A. 1                                       B.                                        C.                                        D. 
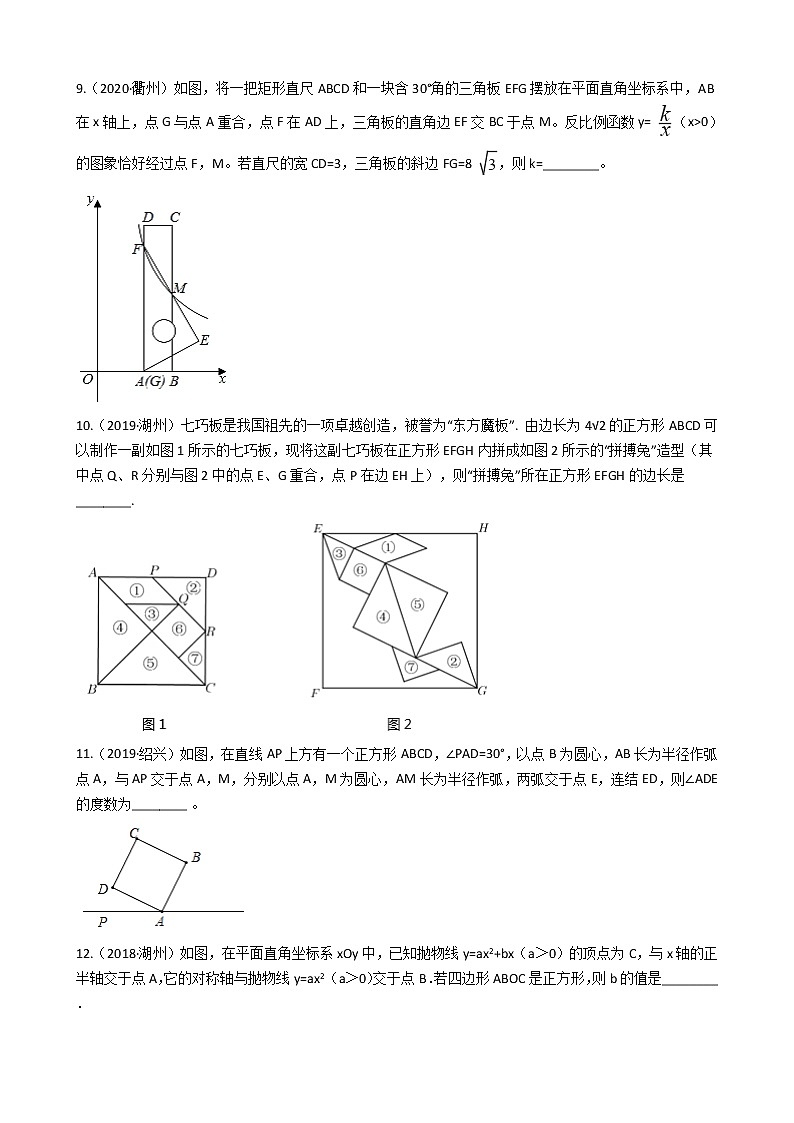
6.（2020·金华·丽水）如图，⊙O是等边△ABC的内切圆，分别切AB，BC，AC于点E，F，D，P是 上一点，则∠EPF的度数是（   ）

A. 65°                                       B. 60°                                       C. 58°                                       D. 50°
7.（2020·金华·丽水）如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH.连结EG，BD相交于点O，BD与HC相交于点P.若GO=GP，则 的值是（   ）

A.                                  B.                                  C.                                  D. 
8.（2019·绍兴）正方形ABCD的边AB上有一动点E，以EC为边作矩形ECFG，且边FG过点D，在点E从点A移动到点B的过程中，矩形ECFG的面积（   ）

A. 先变大后变小                       B. 先变小后变大                       C. 一直变大                       D. 保持不变
二、填空题
9.（2020·衢州）如图，将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中，AB在x轴上，点G与点A重合，点F在AD上，三角板的直角边EF交BC于点M。反比例函数y= （x>0）的图象恰好经过点F，M。若直尺的宽CD=3，三角板的斜边FG=8 ，则k=________。

10.（2019·湖州）七巧板是我国祖先的一项卓越创造，被誉为“东方魔板”. 由边长为4√2的正方形ABCD可以制作一副如图1所示的七巧板，现将这副七巧板在正方形EFGH内拼成如图2所示的“拼搏兔”造型（其中点Q、R分别与图2中的点E、G重合，点P在边EH上），则“拼搏兔”所在正方形EFGH的边长是________.

11.（2019·绍兴）如图，在直线AP上方有一个正方形ABCD，∠PAD=30°，以点B为圆心，AB长为半径作弧点A，与AP交于点A，M，分别以点A，M为圆心，AM长为半径作弧，两弧交于点E，连结ED，则∠ADE的度数为________ 。

12.（2018·湖州）如图，在平面直角坐标系xOy中，已知抛物线y=ax2+bx（a＞0）的顶点为C，与x轴的正半轴交于点A，它的对称轴与抛物线y=ax2（a＞0）交于点B．若四边形ABOC是正方形，则b的值是________．

13.（2018·湖州）如图，已知菱形ABCD，对角线AC，BD相交于点O．若tan∠BAC= ，AC=6，则BD的长是________．

14.（2018·宁波）如图，在菱形ABCD中，AB=2，∠B是锐角，AE⊥BC于点E，M是AB的中点，连结MD，ME．若∠EMD=90°，则cosB的值为________。

15.（2018·宁波）如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连结PM，以点P为圆心，PM长为半径作⊙P．当⊙P与正方形ABCD的边相切时，BP的长为________。

16.（2018·温州）如图，直线 与 轴、 轴分别交于A，B两点，C是OB的中点，D是AB上一点，四边形OEDC是菱形，则△OAE的面积为________．

17.（2018·杭州）折叠矩形纸片ABCD时，发现可以进行如下操作：①把△ADE翻折，点A落在DC边上的点F处，折痕为DE，点E在AB边上；②把纸片展开并铺平；③把△CDG翻折，点C落在直线AE上的点H处，折痕为DG，点G在BC边上，若AB=AD+2，EH=1，则AD=________。

18.（2018·绍兴）等腰三角形ABC中，顶角A为40°，点P在以A为圆心，BC长为半径的圆上，且BP=BA，则∠PBC的度数为________。
三、解答题
19.（2019·嘉兴）如图，在矩形 ABCD中,点 E，F 在对角线BD．请添加一个条件，使得结论“AE=CF”成立，并加以证明．

20.（2018·衢州）如图，在▱ABCD中，AC是对角线，BE⊥AC，DF⊥AC，垂足分别为点E，F。

求证：AE＝CF。
四、作图题
21.（2020·衢州）如图，在5×5的网格中，△ABC的一个顶点都在格点上。

（1）在图1中画出一个以AB为边的 ABDE，使顶点D，E在格点上。
（2）在图2中画出一条恰好平分△ABC周长的直线l（至少经过两个格点）。
五、综合题
22.（2020·衢州）【性质探究】
如图，在矩形ABCD中，对角线AC，BD相交于点O，AE平分∠BAC，交BC于点E。作DF⊥AE于点H，分别交AB，AC于点F，G。

（1）判断△AFG的形状并说明理由。
（2）求证：BF=2OG。
（3）【迁移应用】
记△DGO的面积为S1 ， △DBF的曲积为S2 ， 当 时，求 的值。
（4）【拓展延伸】
若DF交射线AB于点F，【性质探究】中的其余条件不变，连结EF。当△BEF的面积为矩形ABCD面积的 时，请直接写出tan∠BAE的值。
23.（2020·杭州）如图，在正方形ABCD中，点E在BC边上， 连接AE、∠DAE的平分线AG与CD边交于点G，与BC的延长线交于点F，设 =λ(λ>0)。

（1）若AB=2，λ=1，求线段CF的长。
（2）连接EG，若EG⊥AF，
①求证：点G为CD的中点。
②求λ的值。
24.（2020·宁波）如图

（1）【基础巩固】
如图1，在△ABC中，D为AB上一点，∠ACD=∠B.求证： .
（2）【尝试应用】
如图2，在 中，E为BC上一点，F为CD延长线上一点，∠BFE=∠A.若BF=4，BE=3，求AD的长.
（3）【拓展提高】
如图3，在菱形ABCD中，E是AB上一点，F是△ABC内一点，EF∥AC，AC=2EF， ，AE=2，DF=5，求菱形ABCD的边长.
25.（2020·金华·丽水）如图，在平面直角坐标系中，正方形ABOC的两直角边分别在坐标轴的正半轴上，分别过OB，OC的中点D，E作AE，AD的平行线，相交于点F， 已知OB=8.

（1）求证：四边形AEFD为菱形.
（2）求四边形AEFD的面积.
（3）若点P在x轴正半轴上(异于点D)，点Q在y轴上，平面内是否存在点G，使得以点A，P， Q，G为顶点的四边形与四边形AEFD相似？若存在，求点P的坐标；若不存在，试说明理由.
26.（2019·绍兴）如图，矩形ABCD中，AB=a，BC=b，点M，N分别在边AB，CD上，点E，F分别在边BC，AD上，MN，EF交于点P，记k=MN:EF.

（1）若a:b的值为1，当MN⊥EF时，求k的值。
（2）若a:b的值为 ，求k的最大值和最小值。
（3）若k的值为3，当点N是矩形的顶点，∠MPE=60°，MP=EF=3PE时，求a:b为的值。
27.（2019·绍兴）有一块形状如图的五边形余料ABCDE，AB=AE=6，BC=5，∠A=∠B=90°， ∠C=135°. ∠E＞90°.要在这块余料中截取一块矩形材料，其中一条边在AE上，并使所截矩形材料的面积尽可能大。

（1）若所截矩形材料的一条边是BC或AE，求矩形材料的面积。
（2）能否数出比（1）中更大面积的矩形材料？如果能，求出这些矩形材料面积的最大值；如果不能，说明理由.
28.（2019·嘉兴）在 6×6 的方格纸中，点 A，B，C 都在格点上，按要求画图：

（1）在图1中找一个格点D，使以点 A，B，C，D 为顶点的四边形是平行四边形．
（2）在图2中仅用无刻度的直尺，把线段AB 三等分（保留画图痕迹，不写画法）．
29.（2019·湖州）如图，已知在△ABC中，D，E，F分别是AB，BC，AC的中点，连结DF，EF，BF.

（1）求证：四边形BEFD是平行四边形；
（2）若∠AFB＝90°，AB＝6，求四边形BEFD的周长.
30.（2019·宁波）如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F、H在菱形ABCD的对角线BD上.

（1）求证：BG=DE；
（2）若E为AD中点，FH=2，求菱形ABCD的周长。
31.（2019·杭州）如图，已知正方形ABCD的边长为1，正方形CEFG的面积为S1 ， 点E在DC边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为 S2 ， 且S1=S2.

（1）求线段CE的长.
（2）若点日为BC边的中点，连接HD，求证：HD=HG.
32.（2019·嘉兴）小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．

请帮助小波解决“温故”、“推理”、“拓展”中的问题．
（1）温故：如图1，在△ 中， ⊥ 于点 ，正方形 的边 在 上，顶点 ， 分别在 ， 上，若  ， ，求正方形 的边长．
（2）操作：能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作：如图2，任意画△ ，在 上任取一点 ，画正方形 ，使 ， 在 边上， 在△ 内，连结 并延长交 于点N，画 ⊥ 于点 ， ⊥ 交 于点 ， ⊥ 于点 ，得到四边形P ．小波把线段 称为“波利亚线”．
推理：证明图2中的四边形 是正方形．
（3）拓展：在(2)的条件下，于波利亚线 上截取 ，连结 ， (如图3)．当 时，猜想∠ 的度数，并尝试证明．


答案解析部分
一、单选题
1. D
【解答】解：如图，过点M作MH⊥A′R于H，过点N作NJ⊥A′W于J．

由题意△EMN是等腰直角三角形，EM＝EN＝2，MN＝ ，
∵四边形EMHK是矩形，
∴EK＝A′K＝MH＝1，KH＝EM＝2，
∵△RMH是等腰直角三角形，
∴RH＝MH＝1，RM＝ ，同法可证NW＝ ，
由题意AR＝RA′＝A′W＝WD＝4，
∴AD＝AR+RM+MN+NW+DW＝4+ + + +4＝8+ ，
故答案为：D．
【分析】如图，过点M作MH⊥A′R于H，过点N作NJ⊥A′W于J．想办法求出AR，RM，MN，NW，WD即可解决问题．
2. A
【解答】解：对角线相等的四边形推不出是正方形或矩形，
故①→②，①→③错误，
故选项B，C，D错误，
故答案为：A．
【分析】根据对角线相等的四边形推不出是正方形或矩形即可判断．
3. D
【解答】解：由作图知AC＝AD＝BC＝BD，
∴四边形ACBD是菱形，
∴AB平分∠CAD、CD平分∠ACB、AB⊥CD，
不能判断AB＝CD，
故答案为：D．
【分析】根据作图判断出四边形ACBD是菱形，再根据菱形的性质：菱形的对角线平分一组对角、菱形的对角线互相垂直平分可得出答案．
4. D
【解答】 在 中， ， ，
，
四边形 是平行四边形，
．
故答案为： ．
【分析】利用等腰三角形的性质及三角形内角和定理可求出∠C的度数，再利用平行四边形的对角相等，可求出∠E的度数。
5. B
【解答】解：根据题意可知菱形 的高等于 的一半，
菱形 的面积为 ，正方形 的面积为 .
菱形 的面积与正方形 的面积之比是 .
故答案为：B.
【分析】利用30°角所对的直角边等于斜边的一半，就可证得菱形 的高等于 的一半，由此可得到菱形ABC′D′的面积与正方形ABCD的面积，然后求出它们的面积之比。
6. B
【解答】解：连接OE，OF，

∵点EF分别是切点，∴∠OEB=∠OFB=90°，
∵△ABC是等边三角形，∴∠B=60°，
∴∠EOF=360°-∠OEB-∠OFB-∠B=120°，
∴∠P=∠EOF=60°.
故答案为：B.
【分析】连接OE，OF，根据切线的性质可得∠OEB=∠OFB=90°，利用等边三角形的性质可得∠B=60°，根据四边形内角和等于360°，可求出∠EOF的度数，根据圆周角定理可得∠P=∠EOF，据此求出结论.
7. B
【解答】解：设AF=y，BF=x，
∴ 正方形EFGH的边长GH=y-x，
∴EG=GF=（y-x）,
∴ 正方形ABCD的面积为x2+y2 ， 正方形EFGH的面积为（y-x）2 ，
∵ED∥BG，∴∠EDO=∠GBO，
∵ED=BG，∠EOD=∠BOG，
∴△EOD≌GOB，
∴EO=GO，
∴GO=EG=（y-x）,
∵GP=GO，
∴GP=（y-x），
∴GH:GP=，
∴PH：PG=
∵DH∥GB，
∴△DHP∽BGH，
∴， 即得， ∴x=()y
∴ .
故答案为：B.
【分析】设AF=y，BF=x，可得正方形EFGH的边长GH=y-x，即得EG=GF=（y-x）,根据正方形的面积公式可得正方形ABCD的面积为x2+y2 ， 正方形EFGH的面积为（y-x）2 ， 先证△EOD≌GOB，可得EO=GO，可得GO=EG=（y-x），从而可得GP=GO=（y-x），从而可得PH：PG=， 由于DH∥GB，可得△DHP∽BGH，利用相似三角形对应边成比例可得DH：GB=x:y=， 代入正方形的面积进行计算即得结论.
8. D
【解答】解：如图，连接DE，过点E作EH⊥CD于点H，过点D作DM⊥EC于点M

∵正方形ABCD，矩形ECFG
∴四边形AEDH是矩形
∴EH=DC=AD，FC=DM
∴S△DEC= DC·EH= EC·DM
∴DC·EH=EC·DM
∵S矩形ECFG=FC·EC=EC·DM
S正方形ABCD=AD·DC=DC·EH
∴S矩形ECFG=S正方形ABCD
∴在点E从点A移动到点B的过程中，矩形ECFG的面积保持不变。
故答案为：D
【分析】连接DE，过点E作EH⊥CD于点H，过点D作DM⊥EC于点M，易证四边形AEHD是矩形，利用正方形和矩形的性质，可证得EH=DC=AD，FC=DM，再根据同一个三角形的面积相等，可证得DC·EH=EC·DM，因此可得到在点E从点A移动到点B的过程中，矩形ECFG的面积等于正方形ABCD的面积，即可得出答案。
二、填空题
9. 40
【解答】解：过点M作MN⊥AD ， 垂足为N ，

则MN＝AD＝3，
在Rt△FMN中，∠MFN＝30°，
∴FN＝ MN＝3 ，
∴AN＝MB＝8 ﹣3 ＝5 ，
设OA＝x ， 则OB＝x+3，
∴F（x ， 8 ），M（x+3，5 ），
∴8 x＝（x+3）×5 ，
解得，x＝5，
∴F（5，8 ），
∴k＝5×8 ＝40 ．
故答案为：40 ．
【分析】通过作辅助线，构造直角三角形，求出MN ， FN ， 进而求出AN、MB ， 表示出点F、点M的坐标，利用反比例函数k的意义，确定点F的坐标，进而确定k的值即可．
10.
【解答】 解：如图，延长EO交GH于点K，取②中三角形斜边中点J，连结JK，由图1知KJ一定过②中三角形的直角顶点，

由图1可得：
EO=8，OK=2，KJ=4，
∴EK=EO+OK=8+2=10，
在Rt△KGJ中，
∴KG= ，
设正方形EFGH边长为a，则HK=a-2 ，
在Rt△KEH中，
∵EK2=EH2+HK2 ，
即102=a2+（a-2 ）2 ，
解得：a=4 或a=-2 （舍去），
∴正方形EFGH边长为4 .
故答案为：4 .
【分析】由图1可得：EO=8，OK=2，KJ=4，EK=10，在Rt△KGJ中，根据勾股定理求得KG长，
设正方形EFGH边长为a，则HK=a-2 ，在Rt△KEH中，根据勾股定理建立一元二次方程，解之即可求得答案.
11. 15°或45°
【解答】解：如图，

∵正方形ABCD
∴∠DAB=90°，∠BAD=45°，AD=AB
∵∠DAP=30°
∴∠BAM=90°-30°=60°
由题意可知AB=BM
∴△ABM是等边三角形，
∴AM=AB=BM
由题意可知
当点E的位置在直线PA上方，与点B重合，此时∠ADE2=45°；
当点E的位置在直线PA下方，此时点B（E2）与点E1关于直线PA对称，
∴BA=AE,2=AM=AD
∴∠MAE1=60°，∠ADE1=∠AE1D
∴∠DAE1=360°-∠DAB-∠BAM-∠MAE1
=360°-90°-60°-60°
=150°
∴∠ADE1=（180°-150°）÷15°
故答案为： 15°或45°
【分析】根据题意画出图形，利用正方形的性质及作图，可证△ABM是等边三角形，易证AM=AB=BM，就可求出∠BAM的度数，再分情况讨论：当点E的位置在直线PA上方，与点B重合，此时∠ADE2=45°；当点E的位置在直线PA下方，此时点B（E2）与点E1关于直线PA对称，利用轴对称的性质，可得到BA=AE,2=AM=AD，从而可证得∠ADE1=∠AE1D，求出∠MAE1的度数，再利用∠DAE1=360°-∠DAB-∠BAM-∠MAE1 ， 求出∠DAE1的度数，然后利用三角形内角和定理求出∠ADE1的度数即可。
12.﹣2
【解答】解：∵四边形ABOC是正方形，
∴点B的坐标为（- ，- ）．
∵抛物线y=ax2过点B，
∴- =a（- ）2 ，
解得：b1=0（舍去），b2=-2．
故答案为：-2．
【分析】根据正方形的性质得出B点的坐标，根据抛物线上点的坐标特点，将B点坐标代入抛物线y=ax2即可得出方程，求解即可得出b的值。
13.2
【解答】解：∵四边形ABCD是菱形，AC=6，
∴AC⊥BD，OA= AC=3，BD=2OB．
在Rt△OAB中，∵∠AOD=90°，
∴tan∠BAC= ，
∴OB=1，
∴BD=2．
故答案为2．
【分析】根据菱形的性质得出AC⊥BD，OA=AC=3，BD=2OB．在Rt△OAB中根据正切函数的定义得出tan∠BAC=，即可得出OB的长，进而得出BD的长。
14.
【解答】解：延长DM交CB的延长线于H，

∵四边形ABCD为菱形，
∴AB=AD=BC=2,AD∥BC，
∴∠ADM=∠H，
又∵M是AB的中点，
∴AM=BM=1，
在△ADM和△BHM中，
∵ ，
∴△ADM≌△BHM（AAS），
∴DM=HM，AD=BH=2,
∵EM⊥DM，
∴EH=ED,
设BE=x，
∴EH=ED=2+x，
∵AE⊥BC，
∴∠AEB=∠EAD=90°,
∴AE2=AB2-BE2=ED2-AD2,
即22-x2=（2+x）2-22,
化简得：x2+2x-2=0，
解得：x=-1，
在Rt△ABE中，
∴cosB=.

故答案为： .
【分析】延长DM交CB的延长线于H，由菱形的性质和平行线的性质可得：AB=AD=BC=2,∠ADM=∠H；由全等三角形的判定AAS得△ADM≌△BHM，再根据全等三角形的性质得DM=HM，AD=BH=2,根据等腰三角形三线合一的性质可得EH=ED,设BE=x，则EH=ED=2+x，根据勾股定理得AE2=AB2-BE2=ED2-AD2,代入数值解这个方程即可得出BE的长.
15.3或
【解答】解：①如图1，当⊙P与边CD相切时，切点为C，

∴PM=PC=R，
∵M是AB的中点，正方形ABCD的边长为8，
∴BM=4,BP=8-R，
在Rt△PBM中，
∴PM2=PB2+BM2,
即R2=（8-R）2+42 ，
解得：R=5，
∴BP=8-R=8-5=3.
②如图2，当当⊙P与边AD相切时，设切点为K，连结PK，

∴PK⊥AD,
∴四边形ABPK为矩形，
∴PK=PM=8，
∵M是AB的中点，正方形ABCD的边长为8，
∴BM=4,
在Rt△PBM中，
∴PM2=PB2+BM2,
即82=PB2+42 ，
解得：PB=4 ，
综上所述：PB的长度为3或4 .
故答案为：3或4 .
【分析】①如图1，当⊙P与边CD相切时，切点为C，根据切线和正方形的性质得PM=PC=R，BM=4,BP=8-R，在Rt△PBM中，根据勾股定理即可得
R2=（8-R）2+42 ， 解之即可得R，从而求得BP；
②如图2，当当⊙P与边AD相切时，设切点为K，连结PK，根据切线的性质得PK⊥AD,由矩形判定和性质得PK=PM=8，在Rt△PBM中，根据勾股定理即可得82=PB2+42 ， 解之即可得PB长.
16.
【解答】解 ：把x=0代入 y = − x + 4 得出y=4,∴B(0,4);∴OB=4;   ∵C是OB的中点，∴OC=2,∵四边形OEDC是菱形,∴DE=OC=2;DE∥OC,把y=0代入 y = − x + 4 得出x=,∴A(,0);∴OA=,设D(x,) ,∴E(x,-x+2),延长DE交OA于点F，∴EF=-x+2,OF=x,在Rt△OEF中利用勾股定理得：,解得 ：x1=0(舍），x2=；∴EF=1,∴S△AOE=·OA·EF=2.
故答案为：2
【分析】根据直线于坐标轴交点的坐标特点得出,A,B两点的坐标，得出OB，OA的长，根据C是OB的中点，从而得出OC的长，根据菱形的性质得出DE=OC=2;DE∥OC；设出D点的坐标，进而得出E点的坐标，从而得出EF,OF的长，在Rt△OEF中利用勾股定理建立关于x的方程，求解得出x的值，然后根据三角形的面积公式得出答案。
17.或3
【解答】∵当点H在线段AE上时
把△ADE翻折，点A落在DC边上的点F处，折痕为DE，点E在AB边上
∴四边形ADFE是正方形
∴AD=AE
∵AH=AE-EH=AD-1
∵把△CDG翻折，点C落在直线AE上的点H处，折痕为DG，点G在BC边上
∴DC=DH=AB=AD+2
在Rt△ADH中，AD2+AH2=DH2
∴AD2+（AD-1）2=（AD+2）2
解之：AD=3+2 ，AD=3-2 （舍去）
∴AD=3+2
当点H在线段BE上时
则AH=AE-EH=AD+1
在Rt△ADH中，AD2+AH2=DH2
∴AD2+（AD+1）2=（AD+2）2
解之：AD=3，AD=-1（舍去）
故答案为： 或3
【分析】分两种情况：当点H在线段AE上；当点H在线段BE上。根据①的折叠，可得出四边形ADFE是正方形，根据正方形的性质可得出AD=AE，从而可得出AH=AD-1（或AH=AD+1），再根据②的折叠可得出DH=AD+2，然后根据勾股定理求出AD的长。
18.30°或110°
【解答】解：此题分两种情况 ：①点P在AB的左侧，连接PA，如图，

∴BC=PA,∵等腰三角形ABC中，顶角A为40°，∴∠ABC=70º,AB=AC,又∵BP=BA，∴AC=BP,∴四边形APBC是平行四边形，∴AC∥PB,∴∠CAB=∠PBA=40º,∴∠PBC=∠PBA＋∠ABC=110º,
②点P在在AB的右侧，连接PA，如图，

∴BC=PA，,∵等腰三角形ABC中，顶角A为40°，∴∠ABC=70º,AB=AC,又∵BP=BA，∴AC=BP,在△ABP与△BAC中，∵AB=BA,AP=BC,AC=BP,∴△ABP≌△BAC,∴∠ABP=∠BAC=40º,∴∠PBC=∠ABC-∠ABP=30º.
故答案为：30°或110°
【分析】此题分两种情况 ：①点P在AB的左侧，连接PA，根据等腰三角形的性质由等腰三角形ABC中，顶角A为40°，得出∠ABC=70º,AB=AC,又BP=BA，故AC=BP,根据两组对边分别相等的四边形是平行四边形得出：四边形APBC是平行四边形，根据平行四边形的对边平行得出AC∥PB,根据二直线平行内错角相等得出∠CAB=∠PBA=40º,根据∠PBC=∠PBA＋∠ABC得出答案；,②点P在在AB的右侧，连接PA，根据等腰三角形ABC中，顶角A为40°，∴得出∠ABC=70º,AB=AC,又BP=BA，故AC=BP由SSS判断出△ABP≌△BAC,根据全等三角形的对应角相等得出∠ABP=∠BAC=40º,根据∠PBC=∠ABC-∠ABP得出答案。
三、解答题
19. 解:添加条件：BE=DF或DE=BF或 AE∥CF或∠AEB=∠DFC或∠DAE=∠BCF或∠AED-∠CFB或∠BAE-∠DCF或∠DCF+∠DAE=90°等.
若选择BE=DF.
证明：在矩形ABCD中，AB∥CD，AB=CD，
∴∠ABE=∠CDF.
∵BE=DF，
∴△ABE≌△CDF(SAS).
∴AE=CF.
【分析】利用矩形的性质和平行线的性质，易证AB=CD，∠ABE=∠CDE，添加条件要使AE=CF，可证△ABE≌△CDF，因此若利用SAS，则可添加BE=DF或DE=BF，若利用AAS或ASA，可添加另外两组角中的一组角相等，或添加AE∥CF，或添加AE⊥BD，CF⊥BD，证明即可。
20.证明：∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD．
∴∠BAE=∠DCF
∵BE⊥AC，DF⊥AC，
∴∠AEB=∠CFD=90°
∴△ABE≌△CDF
∴AE=CF
【分析】根据平行四边形的性质及平行线的性质，可证得∠BAE=∠DCF，再根据垂直的定义证明∠AEB=∠CFD，利用全等三角形的判定可证得△ABE≌△CDF，然后利用全等三角形的性质，可证得结论。
四、作图题
21. （1）解：如图平行四边形ABDE即为所求（点D的位置还有6种情形可取）．


（2）解：如图，直线l即为所求，

【分析】（1）根据平行四边形的定义画出图形即可（答案不唯一）．（2）利用数形结合的思想解决问题即可．
五、综合题
22. （1）解：如图1中，△AFG是等腰三角形．

理由：∵AE平分∠BAC，
∴∠1＝∠2，
∵DF⊥AE，
∴∠AHF＝∠AHG＝90°，
∵AH＝AH，
∴△AHF≌△AHG（ASA），
∴AF＝AG，
∴△AFG是等腰三角形．

（2）解：如图2中，过点O作OL∥AB交DF于L，则∠AFG＝∠OLG．

∵AF＝AG，
∴∠AFG＝∠AGF，
∵∠AGF＝∠OGL，
∴∠OGL＝∠OLG，
∴OG＝OL，
∵OL∥AB，
∴△DLO∽△DFB，
∴ ，
∵四边形ABCD是矩形，
∴BD＝2OD，
∴BF＝2OL，
∴BF＝2OG．

（3）解：如图3中，过点D作DK⊥AC于K，则∠DKA＝∠CDA＝90°，

∵∠DAK＝∠CAD，
∴△ADK∽△ACD，
∴ ，
∵S1＝ •OG•DK，S2＝ •BF•AD，
又∵BF＝2OG， ，
∴ ，
设CD＝2x，AC＝3x，则AD＝2 x，
∴ ．

（4）tan∠BAE的值为 或
【解答】（4）设OG为a，AG为k。
①如图4，连接EF ， 当点F在线段AB上时，点G在线段OA上

∵AF=AG，BF=2OG，
∴AF=AG=k，BF=2a，
∴AB=k+2a，AC=2（k+a），
∴AD2=[2（k+a）]2-（k+2a）2 ， ∴AD²=3k2+4ka，
由∠ABE=∠DAF-90°，∠BAE=∠ADF，得△ABE∽△DAF，
∴ ，
∴ ，BE=
根据题意得， 10× ×2a× =AD（k+2a），
∴AD2=10ka，
即10ka=3k2+4ka，
∴k=2a，
∴AD=2 a，
∴BE= ，AB＝4a ，
tan∠BAE= =
②如图5，当点F在线段AB的延长线上时，点G在线段OC上，连接EF ．

∵AF=AG，BF=2OG，
∴AF=AG=k，BF=2a，
∴AB=k-2a，AC=2（k-a）
∴AD2＝AC2﹣CD2＝[2（k﹣a）]2﹣（k﹣2a）2＝3k2﹣4ka ，
∵∠ABE＝∠DAF＝90°，∠BAE＝∠ADF ，
∴△ABE∽△DAF ，
∴ ，
∴ ，
∴BE＝ ，
根据题意得，10× ×2a× =AD（k-2a），
∴AD2=10ka
即10ka=3k²-4ka，
∴k= a，
∴AD＝ a ，
∴BE= = a，AB= a
∴tan∠BAE= =
综上可知，tan∠BAE的值为 或 。
【分析】（1）如图1中，△AFG是等腰三角形．利用全等三角形的性质证明即可．（2）如图2中，过点O作OL∥AB交DF于L ， 则∠AFG＝∠OLG ． 首先证明OG＝OL ， 再证明BF＝2OL即可解决问题．（3）如图3中，过点D作DK⊥AC于K ， 则∠DKA＝∠CDA＝90°，利用相似三角形的性质解决问题即可．（4）设OG＝a ， AG＝k ． 分两种情形：①如图4中，连接EF ， 当点F在线段AB上时，点G在OA上．②如图5中，当点F在AB的延长线上时，点G在线段OC上，连接EF ． 分别求解即可解决问题．
23. （1）解：四边形ABCD是正方形，
∴AD∥BC
∴∠DAF=∠F，
又AG平分∠DAE
∴∠DAF=∠EAF
∴∠EAF=∠F，
∴EA=EF
又∵λ=1，AB=BC=2，
∴BE=EC=1，
在Rt△ABE中，由勾股定理得，EA=
∴CF=EF-EC= -1

（2）解：①∵EA=EF，EG⊥AF
∴AG=GF
又∵∠AGD=∠FGC，∠DAG=∠F
∴△DAG≌△CFG
∴DG=CG，
∴点G是CD的中点。
②设CD=2，则CG=1，
由①知，CF=AD=2
由题意△EGC∽△GFC，
∴
∴EC= ，∴BE=
∴λ=
【分析】（1）利用正方形的性质可知AD∥BC，再利用平行线的性质和角平分线的性质，可证得∠EAF=∠F，利用等角对等边可证得EA=EF，结合已知，利用勾股定理求出EA，EC的长，即可求出CF的长。
（2）①利用等腰三角形的性质，可得到AG=GF，再证明△DAG≌△CFG，利用全等三角形的对应边相等，可证得DG=CG，即可证得结论；②利用已知条件易证△EGC∽△GFC，利用相似三角形的性质，求出EC，BE的长，然后求出CE与BE的比值。
24. （1）解： ∵∠ACD=∠B，∠A=∠A
∴△ADC∽△ACB
∴
∴AC2=AD·AB

（2）解：∵四边形ABCD是平行四边形，
∴AD=BC，∠A=∠C，
又∵∠BFE=∠A，
∴∠BFE=∠C，---6分
又∵∠FBE=∠CBF，
∴△BFE∽△BCF，
∴BF2=BE·BC，
∴BC2=
∴AD=

（3）解：如图，分别延长EF，DC相交于点G，

∵四边形ABCD是菱形，
∴AB∥DC，∠BAC= ∠BAD，
∵AC∥EF，
∴四边形A EGC为平行四边形，
∴AC=EG，CG=AE，∠EAC=∠G，
∵∠EDF= ∠BAD，
∴∠EDF=∠BAC，
∴∠EDF=∠G，
又∵∠DEF=∠GED，
∴△EDF∽△EGD，
∴DE2=EF·EG，
又∵EG=AC=2EF，
∴DE2=2EF²，
∴DE= EF，
又∵
∴DG= DF=5 ，
∴DC=DG-CG=5 -2
【分析】（1）利用两个角相等的两个三角形相似，再根据相似三角形的性质列比例式即可得出结果；
（2）由平行四边形的性质得出AD=BC，∠A=∠C，再根据两个角分别相等的两个三角形相似求出 △BFE∽△BCF，于是由对应边成比例可得BF2=BE·BC，则BC的长可求，AD的长也可知；
（3）分别延长EF，DC相交于点G，由两组对边分别平行可得四边形A EGC为平行四边形，可得 △EDF∽△EGD，于是由相似三角形的性质得出DE2=EF·EG，结合EG=AC=2EF, 可得DE=EF，再根据相似三角形的性质列式，两者结合可得求得DG的长， 则DC的长可求.
25. （1）证明：∵DF∥AE，EF∥AD，
∴四边形AEFD是平行四边形.
∵四边形ABOC是正方形，
∴OB＝OC＝AB＝AC，∠ACE＝∠ABD＝Rt∠.
∵点D，E是OB，OC的中点，
∴CE＝BD，
∴△ACE≌△ABD(SAS)，
∴AE＝AD，
∴□AEFD是菱形.

（2）解：如图1，连结DE.

∵S△ABD＝ AB·BD＝ ，
S△ODE＝ OD·OE＝ ，
∴S△AED＝S正方形ABOC－2 S△ABD－ S△ODE
＝64－2 －8＝24，
∴S菱形AEFD＝2S△AED＝48.

（3）解：由图1，连结AF与DE相交于点K，易得△ADK的两直角边之比为1:3.
1）当AP为菱形一边时，点Q在x轴上方，有图2、图3两种情况：
如图2，AG与PQ交于点H，

∵菱形PAQG∽菱形ADFE，
∴△APH的两直角边之比为1:3.
过点H作HN⊥x轴于点N，交AC于点M，设AM=t.
∵HN∥OQ，点H是PQ的中点，
∴点N是OP中点，
∴HN是△OPQ的中位线，
∴ON＝PN＝8－t.
又∵∠1＝∠3＝90°－∠2，∠PNH＝∠AMH＝90°，
∴△HMA∽△PNH，
∴ ＝ ＝ ，
∴HN＝3AM＝3t，
∴MH＝MN－NH＝8－3t.
∵PN＝3MH，
∴8－t =3(8－3t)，解得t＝2.
∴OP＝2ON＝2(8－t)＝12，
∴点P的坐标为(12，0).
如图3，△APH的两直角边之比为1:3.

过点H作HI⊥y轴于点I，过点P作PN⊥x轴交IH于点N，延长BA交IN于点M.
∵∠1＝∠3＝90°－∠2，∠AMH＝∠PNH，
∴△AMH∽△HNP，
∴ ＝ ＝ ，设MH＝t，
∴PN＝3MH＝3t，
∴AM＝BM－AB＝3t－8，
∴HN＝3AM＝3(3t－8) ＝9t－24.
又∵HI是△OPQ的中位线，
∴OP＝2IH，
∴HI＝HN，
∴8＋t＝9t－24，解得 t＝4.
∴OP＝2HI＝2(8＋t)＝24，
∴点P的坐标为(24，0).
2）当AP为菱形一边时，点Q在x轴下方，有图4、图5两种情况：
如图4，△PQH的两直角边之比为1:3.

过点H作HM⊥y轴于点M，过点P作PN⊥HM于点N.
∵MH是△QAC的中位线，
∴HM＝ ＝4.
又∵∠1＝∠3＝90°－∠2，∠HMQ＝∠N，
∴△HPN∽△QHM，
∴ ＝ ＝ ，则PN＝ ＝ ，
∴OM＝ .
设HN＝t，则MQ＝3t.
∵MQ＝MC，
∴3t＝8－ ，解得t＝ .
∴OP＝MN＝4＋t＝ ，
∴点P的坐标为( ，0).
如图5，△PQH的两直角边之比为1:3.

过点H作HM⊥x轴于点M，交AC于点I，过点Q作NQ⊥HM于点N.
∵IH是△ACQ的中位线，
∴CQ＝2HI，NQ＝CI＝4.
∵∠1＝∠3＝90°－∠2，∠PMH＝∠QNH，
∴△PMH∽△HNQ，
∴ ＝ ＝ ＝ ，则MH＝ NQ＝ .
设PM＝t，则HN＝3t，
∵HN＝HI，
∴3t＝8+ ，解得 t＝ .
∴OP＝OM－PM＝QN－PM＝4－t＝ ，
∴点P的坐标为( ，0). 
3）当AP为菱形对角线时，有图6一种情况：

如图6，△PQH的两直角边之比为1:3.
过点H作HM⊥y轴于点M，交AB于点I，过点P作PN⊥HM于点N.
∵HI∥x轴，点H为AP的中点，
∴AI＝IB＝4，∴PN＝4.
∵∠1＝∠3＝90°－∠2，∠PNH＝∠QMH＝90°，
∴△PNH∽△HMQ，
∴ ＝ ＝ ＝ ，则MH＝3PN＝12，HI＝MH－MI＝4.
∵HI是△ABP的中位线，
∴BP＝2HI＝8，即OP＝16，
∴点P的坐标为(16，0).
综上所述，点P的坐标为(12，0)，(24，0)，( ，0)，( ，0)，(16，0).
【分析】（1）根据两组对边分别平行可证四边形AEFD是平行四边形，利用正方形的性质可得OB＝OC＝AB＝AC，∠ACE＝∠ABD＝90°.根据线段中点的定义可得CE＝BD，根据“SAS”可证 △ACE≌△ABD ，可得AE=AD，根据一组邻边相等的平行四边形是菱形即证；
（2）如图1，连结DE. 根据三角形的面积公式求出S△ABD＝  AB·BD＝,16， S△ODE＝  OD·OE=8，利用S△AED＝S正方形ABOC－2 S△ABD－ S△ODE =24，由S菱形AEFD＝2S△AED即可求出结论；
（3）由图1，连结AF与DE相交于点K，易得△ADK的两直角边之比为1:3. 分两种情况讨论：①当AP为菱形一边时，点Q在x轴上方，有图2（△APH的两直角边之比为1:3）；图3(△APH的两直角边之比为1:3).两种情况；②当AP为菱形一边时，点Q在x轴下方，有图4( △PQH的两直角边之比为1:3 )、图5( △PQH的两直角边之比为1:3)两种情况；据此分别解答即可.
26. （1）解:作FH⊥BC，MO⊥CD，如图1，

∵四边形ABCD为正方形，
∴FH=AB，MQ=BC， ∴FH=MQ.
∵MN⊥EF，
∴∠HFE=∠NMO，∠FHE=∠MQN=90°，
∴△FHE≌△MQN， ∴MN=EF，
∴k=1

（2）解:∵a:b=1:2，∴b=2a.
由题意得，2a