人教版九年级下册28.1 锐角三角函数教案配套课件ppt

这是一份人教版九年级下册28.1 锐角三角函数教案配套课件ppt，共37页。PPT课件主要包含了几个重要公式，cosB，点拨设出边长，斜边c，邻边b，对边a，另一条直角边长＝，精讲点拨，探究2，例1计算等内容，欢迎下载使用。

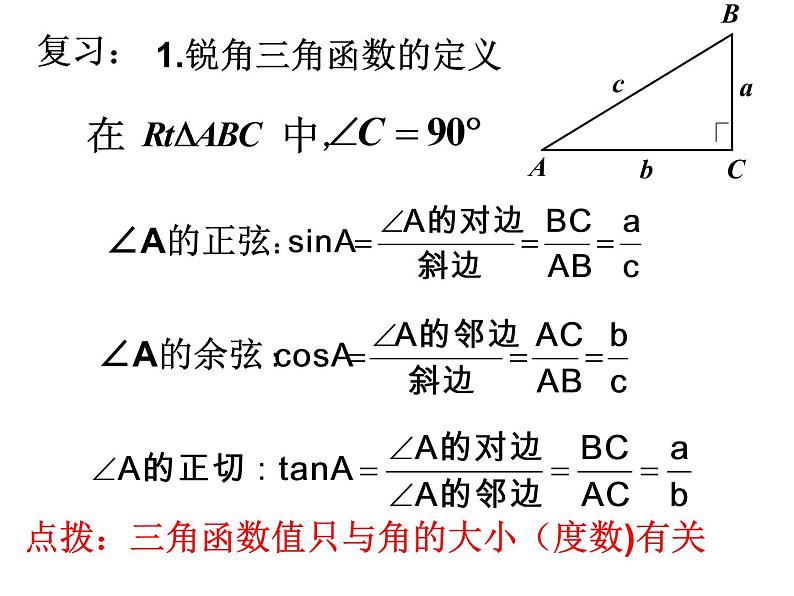
1.锐角三角函数的定义
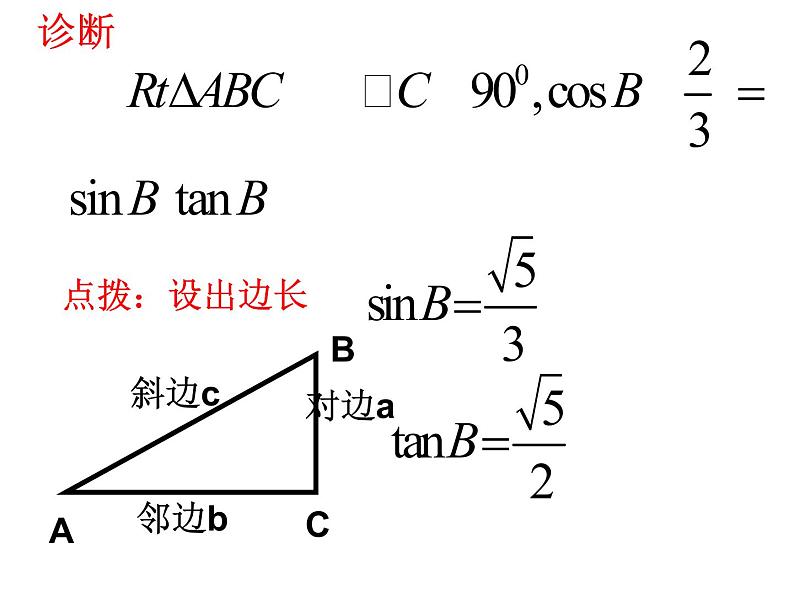
在 中，
点拨：三角函数值只与角的大小（度数)有关
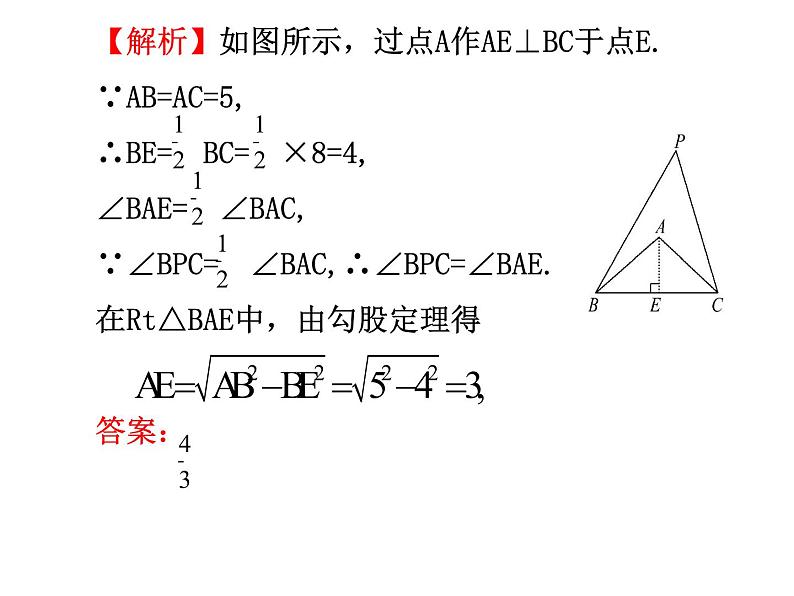
2.(2014·苏州中考)如图,在△ABC中,AB=AC=5,BC=8.若∠BPC= ∠BAC,则tan∠BPC=　　　　.
【解析】如图所示，过点A作AE⊥BC于点E.∵AB=AC=5,∴BE= BC= ×8=4,∠BAE= ∠BAC,∵∠BPC= ∠BAC,∴∠BPC=∠BAE.在Rt△BAE中，由勾股定理得答案：
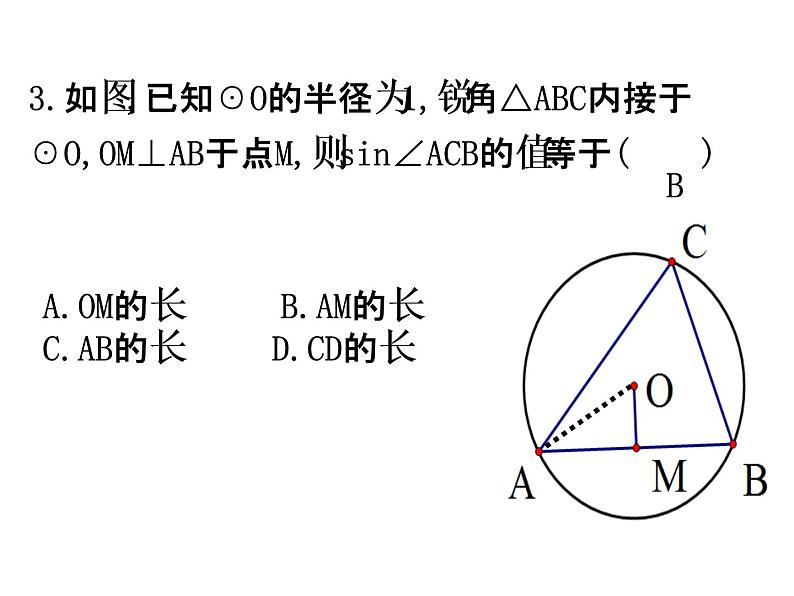
3.如图,已知☉O的半径为1,锐角△ABC内接于☉O,OM⊥AB于点M,则sin∠ACB的值等于(　　)
A.OM的长B.AM的长C.AB的长 D.CD的长
4.如图,已知☉O的半径为1,锐角△ABC内接于☉O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于(　　)
A.OM的长B.2OM的长C.CD的长D.2CD的长
1.能推导并熟记30°，45°，60°角的三角函数值，并能根据这些值说出对应锐角的度数.2.能熟练计算含有30°，45°，60°角的三角函数的运算式.
设30°所对的直角边长为a，那么斜边长为2a
设两条直角边长为a，则斜边长＝
30°、45°、60°角的正弦值、余弦值和正切值如下表：
观察：角度变化、三角函数值变化有什么规律？
观察特殊角的三角函数表，发现规律：
(1)2sin30°－ 3cs60 °
(2)cs²45°+tan60°·cs60°
(3) cs30° sin45°+tan45· cs60°
老师提示:Sin2600表示(sin600)2,cs2600表示(cs600)2,其余类推.
练习：（1）cs260°＋sin260°（2）
解： （1） cs260°＋sin260°
例3 （1）如图，在Rt△ABC中，∠C＝90°， ，求∠A的度数．
（2）如图，已知圆锥的高AO等于圆锥的底面半径OB的 倍，求 a ．
求下列各式的值：（1）1－2 sin30°cs30°（2）3tan30°－tan45°+2sin60°（3）
（1）1－2 sin30°cs30°
（2）3tan30°－tan45°+2sin60°
2. 在Rt△ABC中，∠C＝90°， 求∠A、∠B的度数．
∠B = 90°－ ∠ A = 90°－30°= 60°
拓展【例1】（2012·淮安中考）如图，△ABC中，∠C=90°，点D在AC上，已知∠BDC=45°，BD=10 ，AB=20．1)求∠A的度数．2)求AD的长
【解】（1）在Rt△BDC中，∠BDC的正弦值如何表示？:在Rt△BDC中，sin∠BDC=（2）根据题意，求出BC的长为多少？BC=BD×sin∠BDC=10 ×sin 45°=10 × =10．（3）在Rt△ABC中，根据三角函数值如何求∠A？提示:在Rt△ABC中，∵sin A=∴∠A=30°．
怎样求AD的长？在Rt△ABC中，∴AD=10 -10.由三角函数值求特殊角的方法1.求边长：计算所求角的对边、邻边或斜边.2.求函数值：在直角三角形中，计算所求角的三角函数值.3.求角：根据三角函数值求角的度数.
2.（2012·济宁中考）在△ABC中，若∠A，∠B满足 ，则∠C＝______．【解析】由题意得cs A－ =0，sin B－ =0，∴cs A= sin B= 解得∠A＝60°，∠B＝45°．∴∠C＝180°－∠A－∠B＝180°－60°－45°＝75°．答案:75°
我们学习了30°, 45°, 60°这几类特殊角的三角函数值．
例5 如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为600,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
1.你能得出互为余角的两个锐角A，B正切值的关系吗?2.你能得出一个锐角A的正弦值、余弦值和正切值的关系吗?
仔细观察右表，回答下面问题.
sinA=cs(90°∠A);一个锐角的正弦值等于这个角的余角的余弦值.csA=sin(90°∠A)一个锐角的余弦值等于这个角的余角的正弦值.tanA·tan(90°∠A)=1一个锐角的正切值与这个角的余角的正切值互为倒数.
例4 填空：比较大小