





人教版25.3 用频率估计概率教课内容ppt课件
展开随机事件(不确定事件)
必然事件发生的概率为1, 记作P(必然事件)=1;不可能事件发生的概率为0, 记作P(不可能事件)=0;随机事件(不确定事件)发生的概率介于0~1之 间,即0
2、用列举法求概率有哪几种?
(1)实验的所有结果是有限个(n)(2)各种结果的可能性相等.
当实验的所有结果不是有限个,或各种可能结果发生的可能性不相等时.又该如何求事件发生的概率呢?
1、古典概率条件是什么?用什么方法求?
用列举法可以求一些事件的概率,我们还可以利用多次重复试验,通过统计实验结果去估计概率。
在实验中,每个对象出现的次数与总次数的比值叫频率
用列举法可以求一些事件的概率,我们还可以利用多次重复试验,通过统计试验结果去估计概率.
我们知道,任意抛掷一枚质地均匀的硬币时,“正面向上”和“反面向上”发生的可能性相等,这两个随机事件发生的概率都是0.5。这是否意味着抛掷一枚硬币100次时,就会有50次“正面向上”和50次“反面向上”呢?不妨用试验区进行检验.
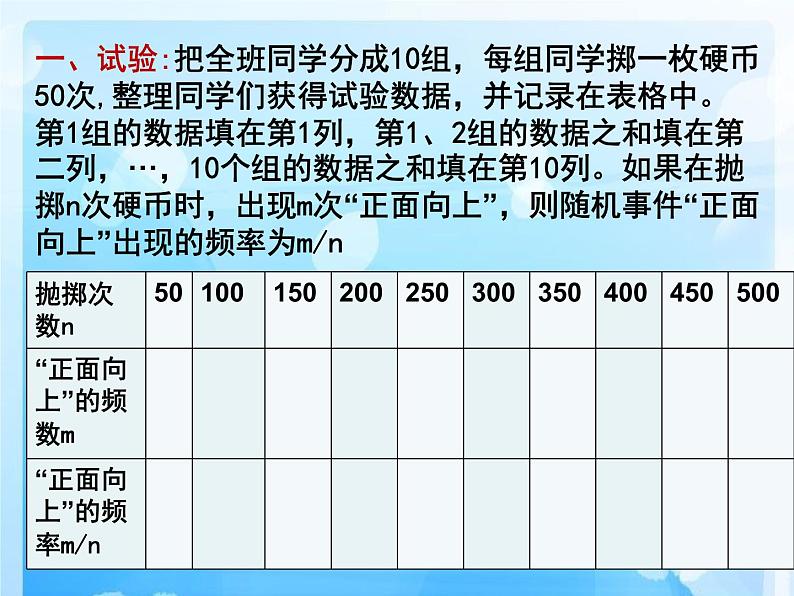
一、试验:把全班同学分成10组,每组同学掷一枚硬币50次,整理同学们获得试验数据,并记录在表格中。第1组的数据填在第1列,第1、2组的数据之和填在第二列,···,10个组的数据之和填在第10列。如果在抛掷n次硬币时,出现m次“正面向上”,则随机事件“正面向上”出现的频率为m/n
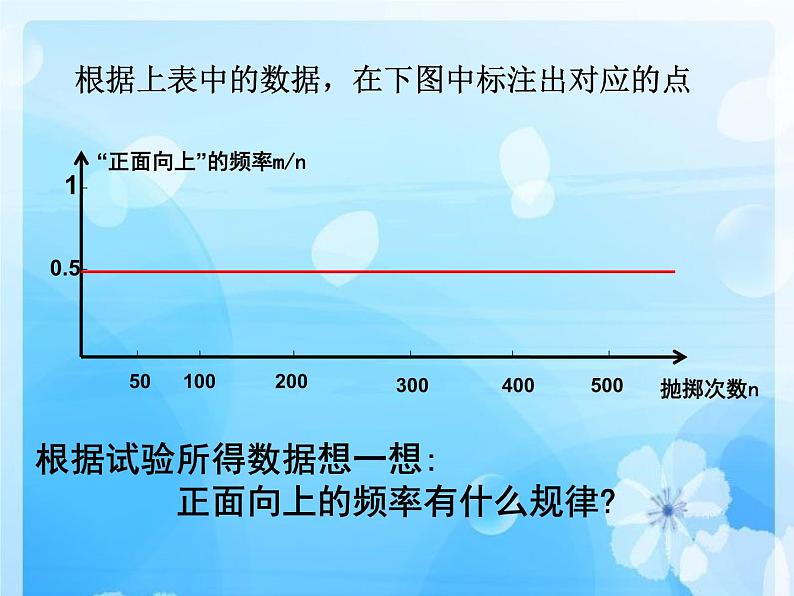
根据试验所得数据想一想: 正面向上的频率有什么规律?
根据上表中的数据,在下图中标注出对应的点
试验1:历史上曾有人作过抛掷硬币的大量重复实验,结果如下表所示
当抛硬币的次数很多时,出现下面的频率值是稳定的,接近于常数0.5,在它附近摆动.
在抛掷一枚硬币时,结果不是“正面向上”就是“反面向上”。因此,从上面提到的试验中也能得到相应的“反面向上”的频率。当“正面向上”的频率稳定于0.5时,“反面向上”的频率呈现什么规律?
“反面向上”的频率也相应地稳定于0.5
瑞士数学家雅各布.伯努利(1654-1705),被公认的概率论的先驱之一,他最早阐明了随着试验次数的增加,频率稳定在概率附近。
实际上,从长期实践中,人们观察到,对一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性。
一般地,在大量重复试验中,如果事件A发生的频率 稳定于某个常数p,那么事件A发生概率的概率
更一般地,即使试验的所有可能结果不是有限个,或各种可能结果发生的可能性不相等我们也可以通过试验的方法去估计一个随机事件发生的概率。只要试验的次数n足够大,频率m/n就作为概率p的估计值。
练习:下表记录了一名球员在罚球线上的投篮结果。
(1)计算表中的投中频率(精确到0.01);(2)这个球员投篮一次,投中的概率大约是多少?(精确到0.1)
问题1 某林业部门要考查某种幼树在一定条件的移植的成活率,应采用什么具体做法?
幼树移植成活率是实际问题中 的一种概率。这个实际问题中的移植实验不属于各种结果可能性相等的类型,所以成活率要由频率去估计。
在同样的条件下,大量的对这种幼树进行移植,并统计成活情况,计算成活的频率。如果随着移植棵树n的越来越大,频率 越来越稳定于某个常数,那么这个常数就可以被当作成活率的近似值
二.新授 思考解答
问题1 某林业部门要考查某种幼树在一定条件的移植的成活率(是实际问题中的一种概率,可理解为成活的概率),应采用什么具体做法?下表是一张模拟的统计表,请补出表中的空缺,并完成表后的填空.
从表可以发现,幼树移植成活的频率在_________左右摆动,并且随着统计数据的增加,这种规律愈加越明显,所以估计幼树移植成活率的概率为________
1.林业部门种植了该幼树1000棵,估计能成活_______棵.
2.我们学校需种植这样的树苗500棵来绿化校园,则至少向林业部门购买约_______棵.
观察在各次试验中得到的幼树成活的频率,谈谈你的看法.
问题2 某水果公司以2元/千克的成本新进了10 000千克的柑橘,如果公司希望这些柑橘能够获得利润5 000元,那么在出售柑橘(已去掉损坏的柑橘)时,每千克大约定价为多少元比较合适?销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行了“柑橘损坏率”统计,并把获得的数据记录在表中,请你帮忙完成此表.
柑橘在运输中会有些随坏,公司必须估算出可能随坏的柑橘总数。以便将随坏的柑橘的成本折算到没有随坏的柑橘的售价中
从表可以看出,柑橘损坏的频率在常数_____左右摆动,并且随统计量的增加这种规律逐渐______,那么可以把柑橘损坏的概率估计为这个常数.如果估计这个概率为0.1,则柑橘完好的概率为_______.
设每千克柑橘的销价为x元,则应有 (x-2.22)×9 000=5 000
因此,出售柑橘时每千克大约定价为2.8元可获利润5 000元.
根据估计的概率可以知道,在10 000千克柑橘中完好柑橘的质量为 10 000×0.9=9 000千克,完好柑橘的实际成本为
某水果公司以2元/千克的成本新进了10000千克柑橘,销售人员首先从所有的柑橘中随机地抽取若干柑橘,进行 了“柑橘损坏率“统计,并把获得的数据记录在下表中
1)同桌合作完成表25-6.(2)根据表中数据填空:这批柑橘损坏的概率是______,则完好柑橘的概率是_______,如果某水果公司以2元/千克的成本进了10000千克柑橘,则这批柑橘中完好柑橘的质量是________,若公司希望这些柑橘能够获利5000元,那么售价应定为_______元/千克比较合适.
为简单起见,我们能否直接把表中500千克柑橘对应的柑橘损坏的频率看作柑橘损坏的频率看作柑橘损坏的概率?
因为500千克柑橘损坏51.54千克,损坏率是0.103,可以近似的估算是柑橘的损坏概率
根据频率稳定性定理,在要求精度不是很高的情况下,不妨用表中的最后一行数据中的频率近似地代替概率.
1.在有一个10万人的小镇,随机调查了2000人,其中有250人看中央电视台的早间新闻.在该镇随便问一个人,他看早间新闻的概率大约是多少?该镇看中央电视台早间新闻的大约是多少人?
解:根据概率的意义,可以认为其概率大约等于250/2000=0.125.该镇约有100000×0.125=12500人看中央电视台的早间新闻.
2.某厂打算生产一种中学生使用的笔袋,但无法确定各种颜色的产量,于是该文具厂就笔袋的颜色随机调查了5000名中学生,并在调查到1000名、2000名、3000名、4000名、5000名时分别计算了各种颜色的频率,绘制折线图如下:
(1)随着调查次数的增加,红色的频率如何变化?
(2)你能估计调查到10000名同学时,红色的频率是多少吗?
估计调查到10000名同学时,红色的频率大约仍是40%左右.
随着调查次数的增加,红色的频率基本稳定在40%左右.
(3)若你是该厂的负责人,你将如何安排生产各种颜色的产量?
红、黄、蓝、绿及其它颜色的生产比例大约为4:2:1:1:2 .
如图,长方形内有一不规则区域,现在玩投掷游戏,如果随机掷中长方形的300次中,有150次是落在不规则图形内.
(1)你能估计出掷中不规则图形的概率吗?
(2)若该长方形的面积为150平方米,试估计不规则图形的面积.
某农科所在相同条件下做了某作物种子发芽率的实验,结果如下表所示:
一般地,1 000千克种子中大约有多少是不能发芽的?
解答:这批种子的发芽的频率稳定在0.9即种子发芽的概率为90%,不发芽的概率为0.1,机不发芽率为10%
所以: 1000×10%=100千克
1000千克种子大约有100千克是不能发芽的.
一个学习小组有6名男生3名女生。老师要从小组的学生中先后随机地抽取3人参加几项测试,并且每名学生都可被重复抽取。你能设计一种实验来估计“被抽取的3人中有2名男生1名女生”的概率的吗?
这种方法是用摸取卡片代替了实际的抽取学生,这样的试验称为模拟实验,你认为上述的模拟实验有道理吗?
我们不妨取9张形状完全相同的卡片,在6张卡片上分别写上1~6的整数表示男生,在其余的3张卡上分别写上7~9的整数表示女生,把9张卡片混合起来并洗均匀.
从卡片中随机抽取1张放回,再抽取1张放回,然后第三次抽取1张,并记录抽取的结果,经重复大量试验,就能够计算相关频率,估计出三人中两男一女的概率.
这样设计有道理吗?
下面的表中给出了一些模拟实验的方法,你觉得这些方法合理吗?若不合理请说明理由
在摸袜子的实验中,如果用6个红色玻璃珠,另外还找了两张扑克牌,可以混在一起做实验吗?
不可以,用不同的替代物混在一起,大大地改变了实验条件,所以结果是不准确的。
注意:实验必须在相同的条件下进行,才能得到预期的结果;替代物的选择必须是合理、简单的。
假设用小球模拟问题的实验过程中,用6个黑球代替3双黑袜子,用2个白球代替1双白袜子:(1)有一次摸出了2个白球,但之后一直忘了把它们放回去,这会影响实验结果吗?
有影响,如果不放回,就不是3双黑袜子和1双白袜子的实验,而是中途变成了3双黑袜子实验,这两种实验结果是不一样的。
(2)如果不小心把颜色弄错了,用了2个黑球和6个白球进行实验,结果会怎样?
小球的颜色不影响恰好是一双的可能性大小
2020-2021学年25.3 用频率估计概率课文课件ppt: 这是一份2020-2021学年25.3 用频率估计概率课文课件ppt,共41页。PPT课件主要包含了问题提出,古典概型,互斥关系,A+B+C,无数个,理论迁移,小结作业,抽签法,用Excel演示,知识迁移等内容,欢迎下载使用。
人教版九年级上册25.3 用频率估计概率评课ppt课件: 这是一份人教版九年级上册25.3 用频率估计概率评课ppt课件,文件包含精选备课2021秋人教版数学九年级上册253用频率估计概率课件pptx、精选备课2021秋人教版数学九年级上册253用频率估计概率学案docx、精选备课2021秋人教版数学九年级上册253用频率估计概率教学设计docx、精选备课2021秋人教版数学九年级上册253用频率估计概率练习docx等4份课件配套教学资源,其中PPT共30页, 欢迎下载使用。
2021学年25.3 用频率估计概率授课课件ppt: 这是一份2021学年25.3 用频率估计概率授课课件ppt,共25页。













