初中人教版24.3 正多边形和圆备课ppt课件

这是一份初中人教版24.3 正多边形和圆备课ppt课件，共20页。PPT课件主要包含了活动2，∴∠A∠B，中心角，因此亭子地基的周长，亭子地基的面积，连接OB则OBR，边心距＝OD，当堂测评，边心距等内容，欢迎下载使用。

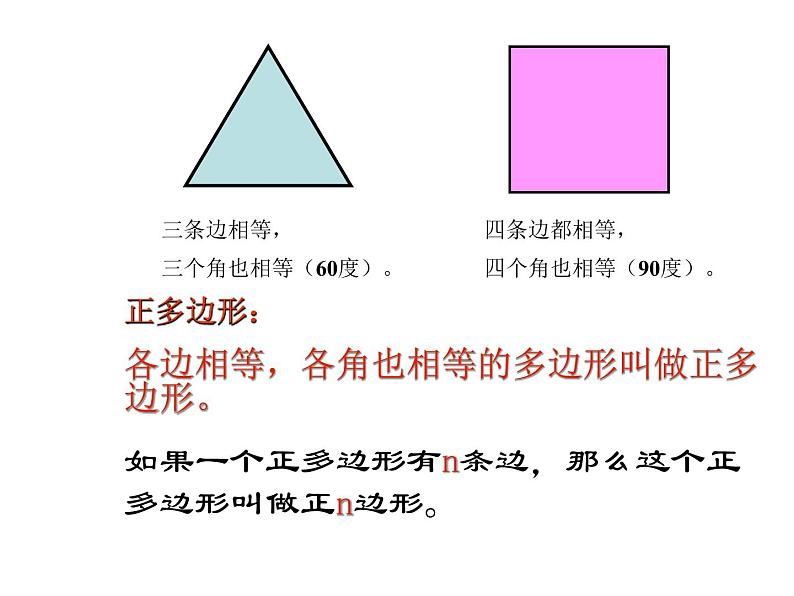
正多边形：各边相等，各角也相等的多边形叫做正多边形。如果一个正多边形有n条边，那么这个正多边形叫做正n边形。
三条边相等，三个角也相等（60度）。
四条边都相等，四个角也相等（90度）。
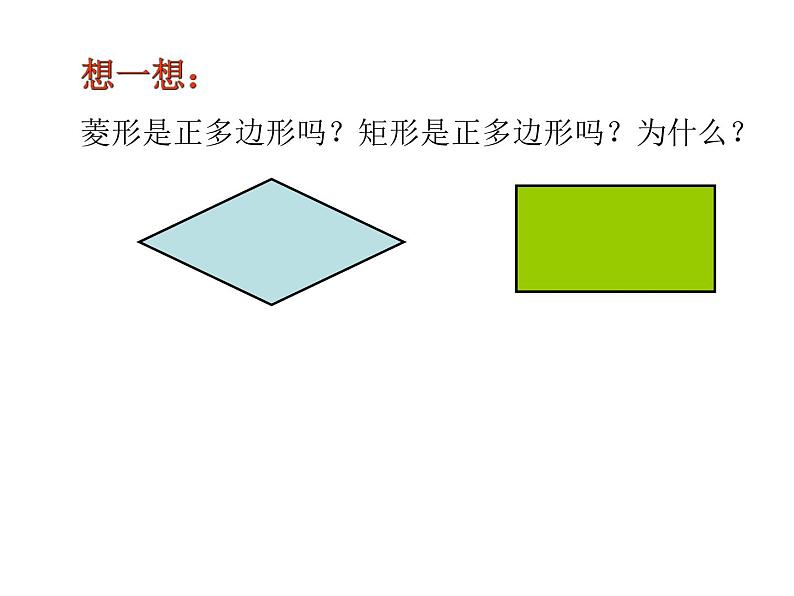
想一想：菱形是正多边形吗？矩形是正多边形吗？为什么？
你知道正多边形与圆的关系吗？
把一个圆分成n等份,顺次连接各分点就可以作出这个圆的内接正n边形,这个圆就是这个正多边形的外接圆.
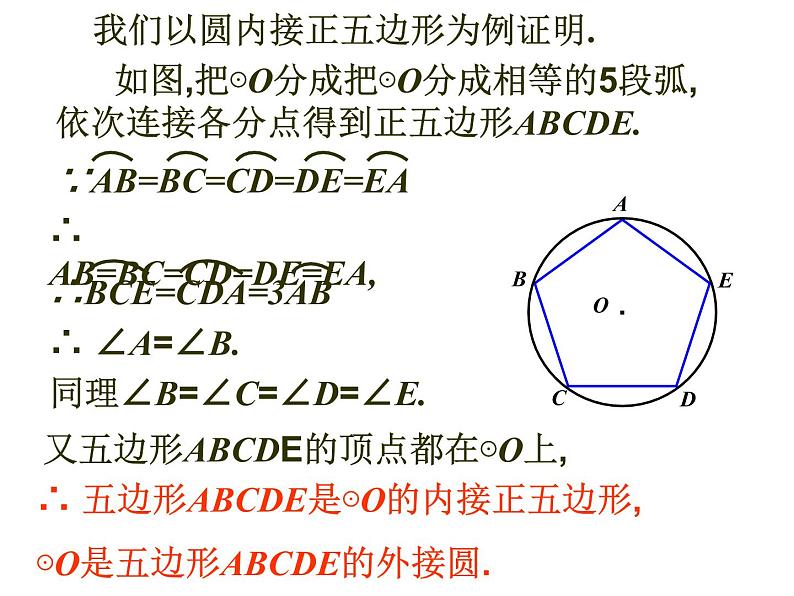
如图,把⊙O分成把⊙O分成相等的5段弧,依次连接各分点得到正五边形ABCDE.
∴ AB=BC=CD=DE=EA,
同理∠B=∠C=∠D=∠E.
又五边形ABCDE的顶点都在⊙O上,
∴ 五边形ABCDE是⊙O的内接正五边形, ⊙O是五边形ABCDE的外接圆.
我们以圆内接正五边形为例证明.
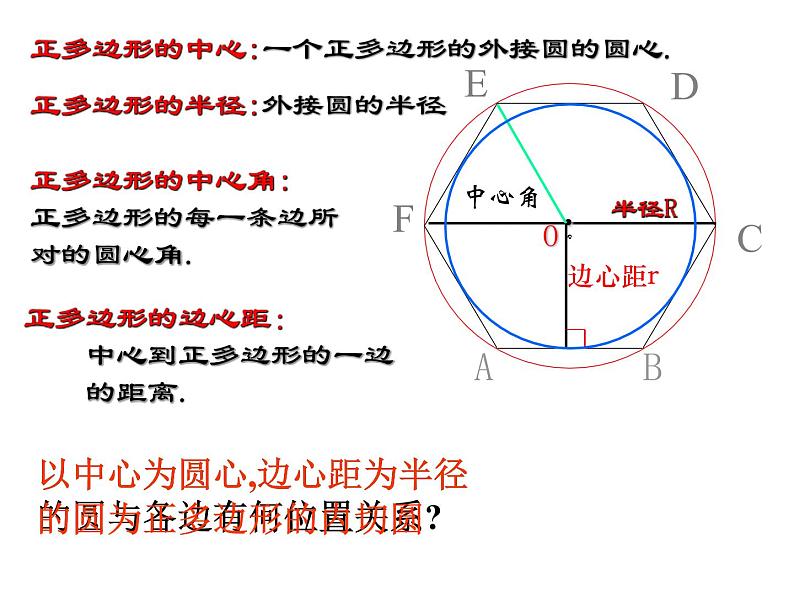
以中心为圆心,边心距为半径的圆与各边有何位置关系?
正多边形的中心:一个正多边形的外接圆的圆心.
正多边形的半径:外接圆的半径
正多边形的中心角:正多边形的每一条边所对的圆心角.
正多边形的边心距： 中心到正多边形的一边 的距离.
以中心为圆心,边心距为半径的圆为正多边形的内切圆
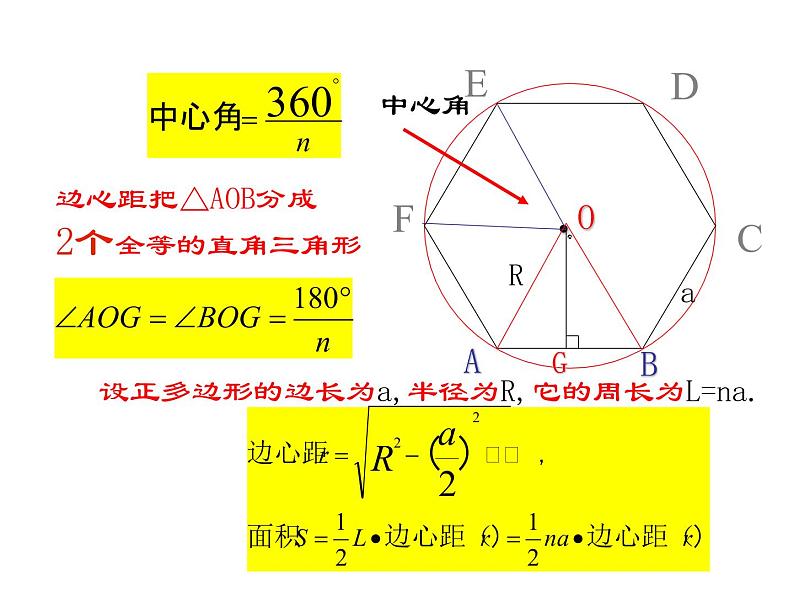
边心距把△AOB分成2个全等的直角三角形
设正多边形的边长为a,半径为R,它的周长为L=na.
例 有一个亭子,它的地基半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).
l =4×6=24(m).
利用勾股定理,可得边心距
练习：分别求出半径为R的圆内接正三角形，正方形的边长，边心距和面积.
解：作等边△ABC的BC边上的高AD,垂足为D
在Rt△OBD中,∠OBD=30°,
解：连接OB，OC 作OE⊥BC垂足为E， ∠OEB=90° ∠OBE= ∠ BOE=45°
在Rt△OBE中为等腰直角三角形
3、正多边形都是轴对称图形，一个正n边形共有n条对称轴，每条对称轴都通过n边形的中心。
4、边数是偶数的正多边形还是中心对称图形，它的中心就是对称中心。
　1、正方形ABCD的外接圆圆心O叫做正方形ABCD的______．　2、正方形ABCD的内切圆⊙O的半径OE叫做正方形ABCD的______．　3、若正六边形的边长为1，那么正六边形的中心角是____度，半径是___，边心距是 ，它的每一个内角是______．　4、正n边形的一个外角度数与它的______角的度数相等．
5.正多边形一定是 对称图形,一个正n边形共有 条对称轴,每条对称轴都通过 ;如果一个正n边形是中心对称图形,n一定是 数.6.将一个正五边形绕它的中心旋转,至少要旋转 度,才能与原来的图形位置重合.7.两个正三角形的内切圆的半径分别为12和18,则它们的周长之比为 ,面积之比为 .
8.下列说法中正确的是( )A.平行四边形是正四边形 B. 矩形是正四边形C. 菱形是正四边形 D. 正方形是正四边形9. 下列命题中,真命题的个数是( )①各边都相等的多边形是正多边形; ②各角都相等的多边形是正多边形;③正多边形一定是中心对称图形; ④边数相同的正多边形一定全等.A.1 B.2 C. 3 D. 4
10.已知正n边形的一个外角与一个内角的比为1﹕3,则n等于( ) A. 4 B. 6 C. 8 D. 12 11. 如果一个正多边形绕它的中心旋转90°就和原来的图形重合,那么这个正多边形是( ) A.正三角形 B.正方形 C.正五边形 D.正六边形
12.正方形ABCD的外接圆圆心O叫做正方形ABCD的
13.正方形ABCD的内切圆的半径OE叫做正方形ABCD的
14、⊙O是正五边形ABCDE的外接圆，弦AB的弦心距OF叫正五边形ABCDE的 　　　　，它是正五边形ABCDE的　　　　　圆的半径。
15、 ∠AOB叫做正五边形ABCDE的　　　　角，它的度数是