





人教版九年级上册23.2.2 中心对称图形教学演示课件ppt
展开23.2.2 中心对称图形
(1)了解中心对称图形的概念,会判断一个图形是否为中心对称图形. (2)知道中心对称图形和两个图形成中心对称、轴对称图形和中心对称图形的联系与区别. 感悟类比方法在研究数学问题中的作用.
探究点一 中心对称图形的概念
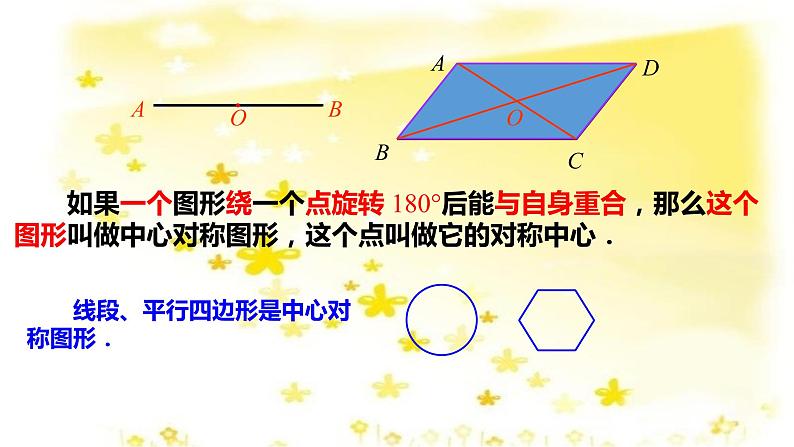
(1)如图,将线段 AB 绕它的中点旋转 180°,你有什么发现?
可以发现:线段 AB 绕它的中点旋转 180°后与它 本身重合.
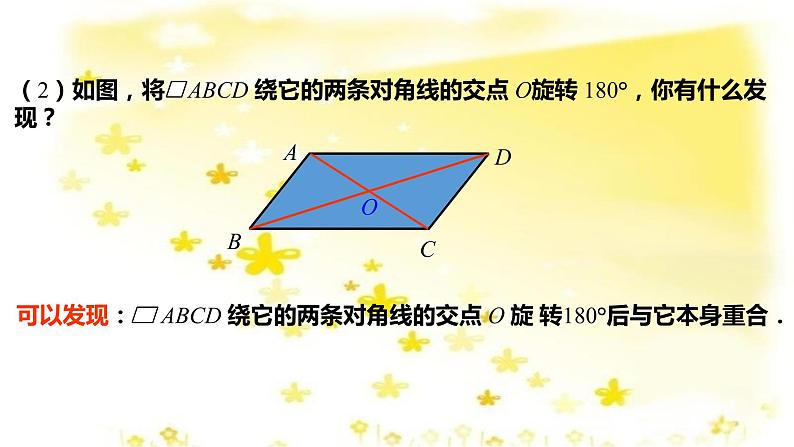
(2)如图,将 ABCD 绕它的两条对角线的交点 O旋转 180°,你有什么发现?
线段、平行四边形是中心对称图形.
如果一个图形绕一个点旋转 180°后能与自身重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
【思考】判断一个图形是否是中心对称图形的关键是什么?
旋转前后的图形完全重合
图形沿轴对折(翻转180°)
图形绕对称中心旋转180°
翻转前后的图形完全重合
轴对称图形与中心对称图形的区别
如图的汽车标志中,哪些是中心对称图形?再举出几个中心对称图形的实例 ?
例1(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形.(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形.(3)选取1个涂上阴影,使4个阴影小正方形组成一个既是轴对称图形,又是中心对称图形.
1.下列图形中,既是轴对称图形又是中心对称图形的是( ) A. B. C. D.2.下列图形中,是中心对称图形,但不是轴对称图形的是( )A.正方形 B.矩形 C.菱形 D.平行四边形
3.下列图形中,是轴对称图形但不是中心对称图形的是( )4. 在线段、等腰梯形、平行四边形、矩形、正六边形、圆、正方形、等边三角形中,既是轴对称图形,又是中心对称图形的图形有( ) A. 3个 B.4个 C.5个 D.6个
例2 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为_______.
解析:由于矩形是中心对称图形,所以依题意可知△BOF与△DOE关于点O成中心对称,由此图中阴影部分的三个三角形就可以转化到直角△ADC中,易得阴影部分的面积为3.
(1)中心对称图形的对称点连线都经过________
(2)中心对称图形的对称点连线被____________
中心对称图形上的每一对对称点所连成的线段都被对称中心平分.
如何寻找中心对称图形的对称中心?
画一画1.下图是中心对称图形的一部分及对称中心,请你补全它的另一部分.
2.如图,有一个平行四边形请你用无刻度的直尺画一条直线把他们分成面积相等的两部分,你怎么画?
过对称中心的直线可以把中心对称图形分成面积相等的两部分.
例3 请你用无刻度的直尺画一条直线把他们分成面积相等的两部分,你怎样画?
1.下列图案都是由字母“m”经过变形、组合 而成的,其中不是中心对称图形的是( )
2.下列图形中既是轴对称图形又是中心对称图形的是 ( )A . 角 B. 等边三角形 C . 线段 D . 平行四边形
3.从一副扑克牌中抽出如下四张牌,其中是中 心对称图形的有( )
A.1 张 B.2 张 C.3 张 D.4 张
4.观察图形,并回答下面的问题:①哪些只是轴对称图形?②哪些只是中心对称图形?③哪些既是轴对称图形,又是中心对称图形?
5.世界上因为有了圆的图案,万物才显得富有生机,以下来自现实生活的图形中都有圆,它们看上去是那么美丽与和谐,这正是因为圆具有 轴对称和中心对称性.
请问以下三个图形中是轴对称图形的有 ,是中心对称图形的有 .
6.图中网格中有一个四边形和两个三角形,(1)请你先画出三个图形关于点O的中心对称图形;
(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形对称轴的条数;这个整体图形至少旋转多少度与自身重合?
绕着内部一点旋转180度能与本身重合的图形
经过对称中心的直线把原图形分成面积相等的两部分
美丽的中心对称图形在建筑物和工艺品等领域非常常见
初中数学人教版九年级上册23.2.2 中心对称图形完美版课件ppt: 这是一份初中数学人教版九年级上册23.2.2 中心对称图形完美版课件ppt,共37页。
初中数学人教版九年级上册23.2.2 中心对称图形教课内容课件ppt: 这是一份初中数学人教版九年级上册23.2.2 中心对称图形教课内容课件ppt,共26页。PPT课件主要包含了新课导入,讲授新课,当堂练习,课堂小结等内容,欢迎下载使用。
初中数学人教版九年级上册23.2.2 中心对称图形示范课课件ppt: 这是一份初中数学人教版九年级上册23.2.2 中心对称图形示范课课件ppt,共21页。PPT课件主要包含了课堂讲解,课时流程,逐点导讲练,课堂小结,课后作业,知识点,中心对称图形的定义,中心对称图形的性质,中心对称图形的作图等内容,欢迎下载使用。













