初中数学人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.2 垂直于弦的直径课文配套ppt课件

这是一份初中数学人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.2 垂直于弦的直径课文配套ppt课件，共36页。PPT课件主要包含了复习回顾等内容，欢迎下载使用。

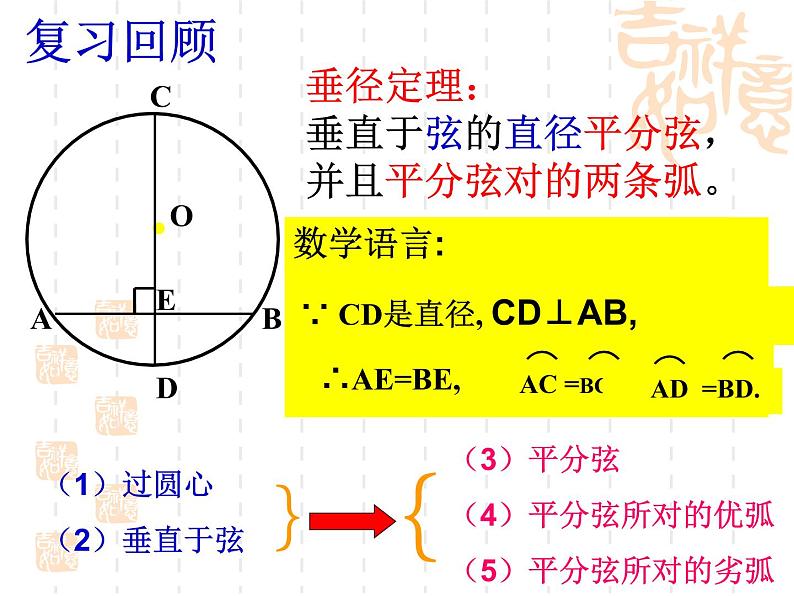
垂径定理：垂直于弦的直径平分弦，并且平分弦对的两条弧。
（1）过圆心（2）垂直于弦
（3）平分弦（4）平分弦所对的优弧（5）平分弦所对的劣弧
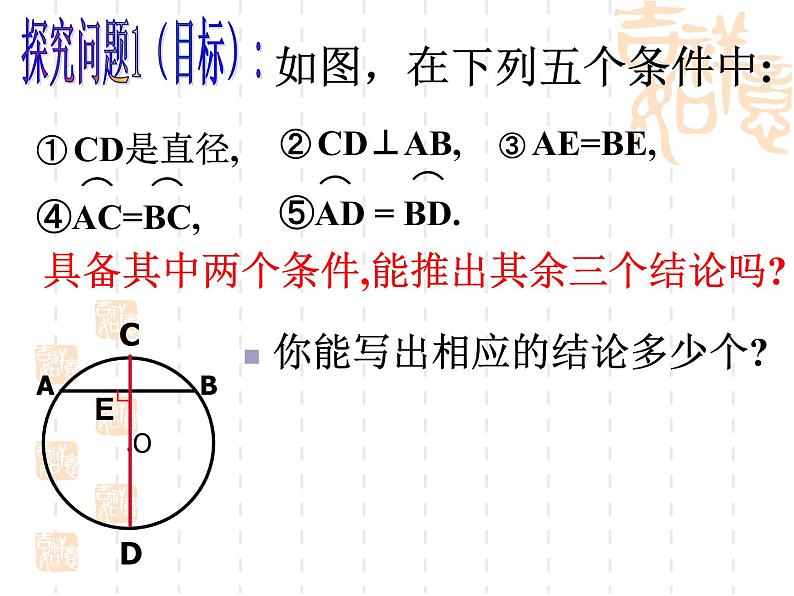
如图，在下列五个条件中:
具备其中两个条件,能推出其余三个结论吗?
你能写出相应的结论多少个?
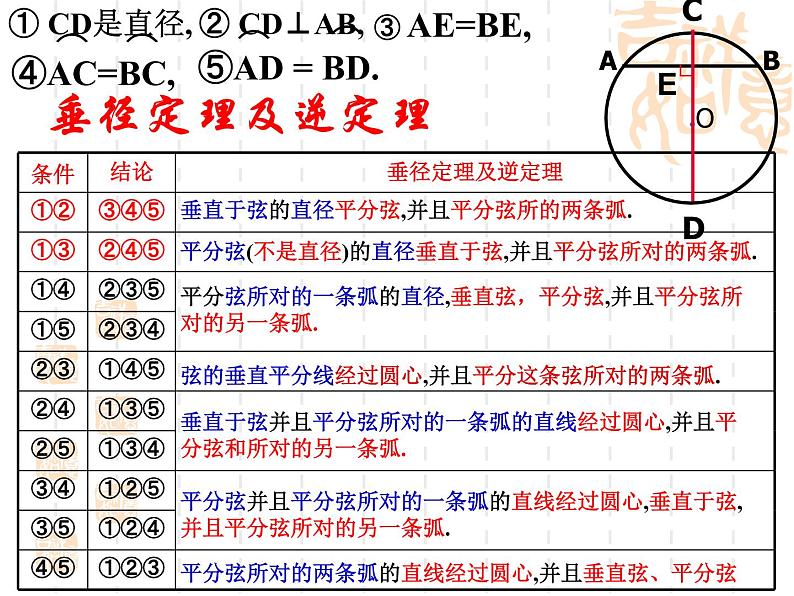
垂直于弦的直径平分弦,并且平分弦所的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
平分弦所对的一条弧的直径,垂直弦，平分弦,并且平分弦所对的另一条弧.
弦的垂直平分线经过圆心,并且平分这条弦所对的两条弧.
垂直于弦并且平分弦所对的一条弧的直线经过圆心,并且平分弦和所对的另一条弧.
平分弦并且平分弦所对的一条弧的直线经过圆心,垂直于弦,并且平分弦所对的另一条弧.
平分弦所对的两条弧的直线经过圆心,并且垂直弦、平分弦.
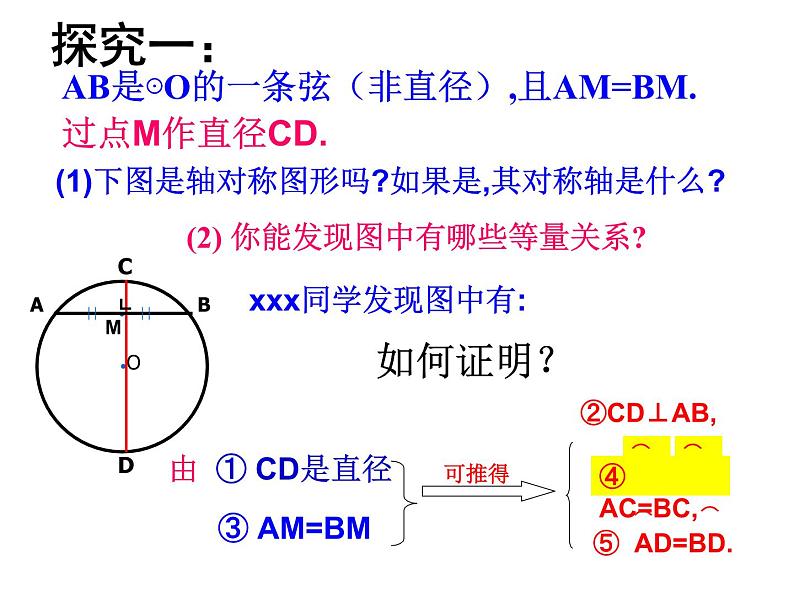
AB是⊙O的一条弦（非直径）,且AM=BM.
(2) 你能发现图中有哪些等量关系?
(1)下图是轴对称图形吗?如果是,其对称轴是什么?
xxx同学发现图中有:
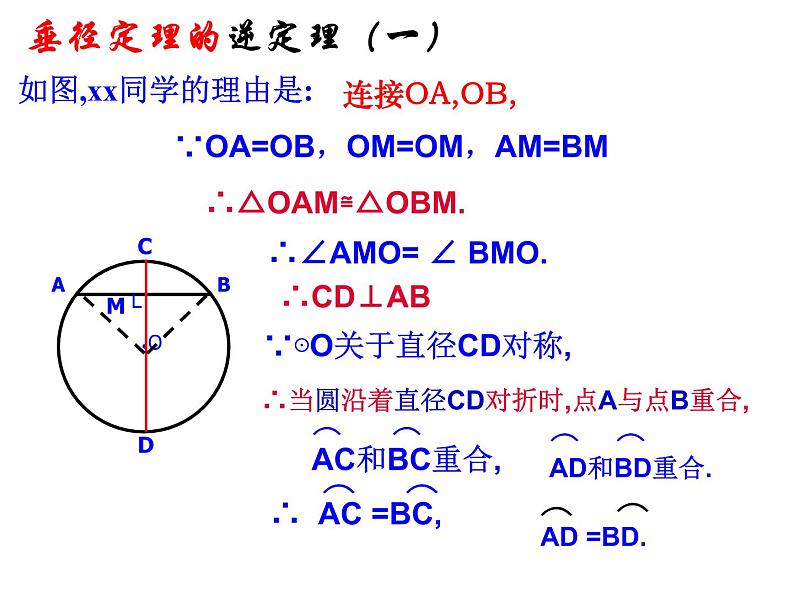
如图,xx同学的理由是:
∵OA=OB，OM=OM，AM=BM
∴△OAM≌△OBM.
∴∠AMO= ∠ BMO.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
垂径定理的逆定理（一）
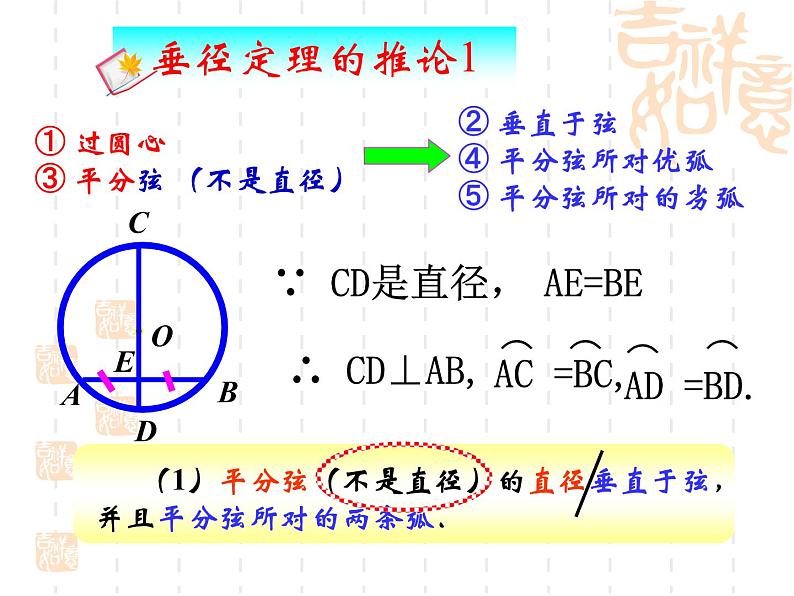
① 过圆心 ③ 平分弦 （不是直径）
② 垂直于弦④ 平分弦所对优弧 ⑤ 平分弦所对的劣弧
（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．
∵ CD是直径，
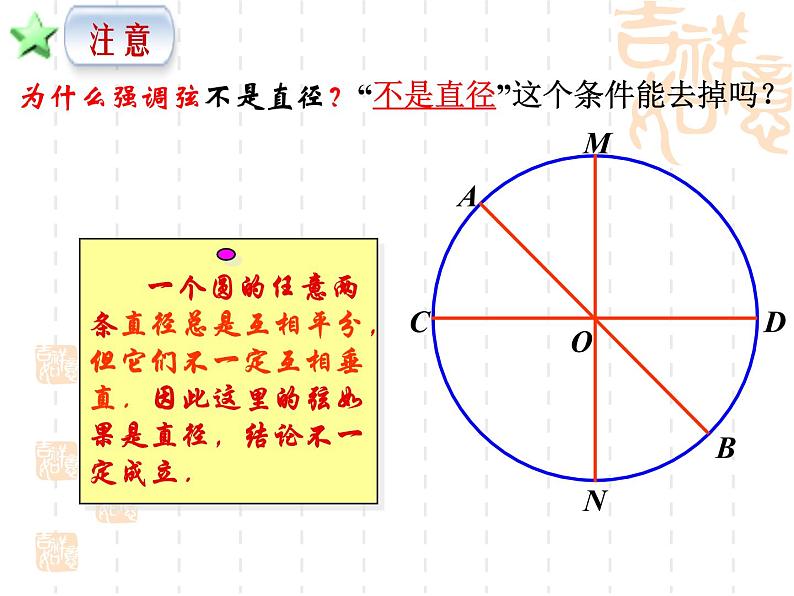
一个圆的任意两条直径总是互相平分，但它们不一定互相垂直．因此这里的弦如果是直径，结论不一定成立．
为什么强调弦不是直径？“不是直径”这个条件能去掉吗？
① 直径过圆心 ④ 平分弦所对优弧
③ 平分弦 ② 垂直于弦⑤ 平分弦所对的劣弧
（2）平分弦所对的一条弧的直径，垂直弦、平分弦，并且平分弦所对的另一条弧．
① 直径过圆心 ⑤ 平分弦所对的劣弧
③ 平分弦 ④ 平分弦所对优弧② 垂直于弦
② 垂直于弦③ 平分弦
① 直径过圆心 ④ 平分弦所对优弧 ⑤ 平分弦所对的劣弧
（3）弦的垂直平分线 经过圆心，并且平分弦所对的两条弧．
(4)若 ，CD是直径,则 、 、 .
(1)若CD⊥AB, CD是直径, 则 、 、 .
(2)若AM=MB, CD是直径, 则 、 、 .
(3)若CD⊥AB, AM=MB, 则 、 、 .
填空：1、如图：已知AB是⊙O的直径，弦CD与AB相交于点E，若_____________________________________________________，则CE=DE（只需填写一个你认为适当的条件）2、如图：已知AB是⊙O的弦，OB=4cm，∠ABO=300，则O到AB的距离是___________cm，AB=_________cm.
（1）平分弦的直径，平分这条弦所对的弧。
（2）平分弦的直线，必定过圆心。
（3）一条直线平分弦（这条弦不是直径）， 那么这 条直线垂直这条弦。
(4)弦的垂直平分线一定是圆的直径。
（5）平分弧的直线，平分这条弧所对的 弦。
（6）弦垂直于直径，这条直径就被弦平分。
（7）平分弦的直径垂直于弦
问题3、如图，已知⊙O中，弦AB的长为8㎝，圆心O到AB的距离（弦心距）为3 ㎝，求圆O的半径。
（2）在半径为5 ㎝的圆O中，有长8 ㎝ 的弦AB，求点O与AB的距离。　　
（3）在半径为5 ㎝的圆O中，圆心O 到弦AB的距离为3 ㎝，求AB的长。
d + h = r
a、d、r、h之间的关系是
(4)⊙O中， 直径FG ⊥弦AB于E，且AB的长为8㎝，EF长h为2 ㎝，求⊙O的半径。
对于一个圆中的弦长a、弦心距d、圆半径r，弓高h这四个量中，只要已知其中任意两个量，就可以求出其他两个量。
作垂径，连半径是圆中常用的辅助线。垂径定理和勾股定理相结合，构造直角三角形，可解决计算弦长、半径、弦心距等问题．
半径、弦长、弦心距、弓形高“知二求二”
1.如图，水平放置的一个油管的截面半径为 13cm，其中有油部分油面宽AB=24cm，则截面上有油部分油面高CD= ——————
半径、弦长、弓形的高、圆心到弦的距离
已知：在⊙O中，弦AB //CD， 求证：
证明：过点O作OM ⊥AB于E，交⊙ O于M，并反向延长交CD于F
垂径定理的推论 圆的两条平行弦所夹的弧相等.
已知⊙O的直径是10 cm，弦AB=8 cm ，弦CD//AB且CD=6cm，（1）请在图中画出CD可能的位置（2）求弦AB与CD之间的距离。
如图，⊙O的直径为10，弦AB=8，P是弦AB上一个动点，求OP的取值范围.
我发现了…… 我学会了…… 我的体会是…… 我的困难是…… 我……
Summary resnsideratin
２、垂径定理及其推论的图式
根据垂径定理与推论可知：对于一个圆和一条直线来说，如果具备：① 经过圆心 ② 垂直于弦 ③ 平分弦 ④平分弦所对的优弧 ⑤平分弦所对的劣弧。那么，由五个条件中的任何两个条件都可以推出其他三个结论。“知二推三”。注意:当具备了(1)(3)时,应对另一条弦增加″不是直径”的限制.
1、圆是轴对称图形，其对称轴是任意一条过圆心的直线（或直径所在直线．）
　　　　 垂直于弦的直径平分这条弦，并且平分弦所对的弧．
　　　　　　　　　　　
3、在圆中解决有关弦的问题时，经常是过圆心作弦的垂线段，连结半径等辅助线，为应用垂径定理创造条件.
7.如图，点A、B是⊙O上两点，AB=10，点P是⊙ O上的动点，（P与A，B不重合），连接AP、PB，过点O分别OE⊥AP于E，OF⊥PB于F，则EF= ——。
如图所示，已知⊙O的直径为4，M是弧AB的中点，MN为玄且MN=2√3，MN交AB于点P，求∠APM的度数．
解：连接OM交AB于点E，∵M是弧的中点，∴OM⊥AB于E．过点O作OF⊥MN于F，由垂径定理得：
2次。 把AB放在圆上不同的位置，分别沿CD作两条直线，其交点就是圆心。 其原理为：弦的垂直平分线过圆心。
思考：一条弦的垂直平分线必过圆心吗？
再想一想：用什么方法能找出圆的圆心呢？
如图，CD所在的直线垂直平分线段AB，利用这样的工具，最少使用____次，可以找到图形工件的圆心？为什么？
如图所示，要把破残的圆片复制完整．已知弧上的三点A、B、C．（1）用尺规作图法找出 BAC 所在圆的圆心．（保留作图痕迹，不写作法）（2）设△ABC是等腰三角形，底边BC=8cm，腰AB=5cm．求圆片的半径R．
考点：垂径定理；等腰三角形的性质；勾股定理；作图．分析：（1）作图思路：可根据AB，AC的垂直平分线来确定圆心．解答：（1）分别作AB、AC的垂直平分线，设交点为O则O为所求圆的圆心
解答： （2）连接AO交BC于E，∵AB=AC∴AE⊥BC，BE=1/2 BC=4在Rt△ABE中，AE= √AB2−BE2 = √52−42 ＝3设⊙O的半径为R，在Rt△BEO中OB2=BE2+OE2，即R2=42+（R-3）2∴R2=16+R2-6R+9∴R=25/6 （cm）所以所求圆的半径为25/6 cm．
考点：垂径定理；等腰三角形的性质；勾股定理；作图．
分析：（2）本题可通过构建直角三角形来求解．连接AO交BC于E．先求出AE的值，然后在直角三角形OBE中，用半径表示出OE，OB，然后根据勾股定理求出半径的值．
等分弧时一定要作弧所夹弦的垂直平分线．
3． 作AC、BC的垂直平分线．
4． 三条垂直平分线交于一点O．
作弦AB、AC及它们的垂直平分线m、n，交于O点；以O为圆心，OA为半径作圆．
弦的垂直平分线经过圆心，并且平分弦所对的两条弧．
问题 ：你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m，你能求出赵洲桥主桥拱的半径吗？
赵州桥主桥拱的半径是多少？
的中点，CD就是拱高。
AB=37.4，CD=7.2 ，∴AD=18.7，设OA=OC=R
OD=OC-CD=R-7.2.
在Rt△AOD中，OA2 = AD2 + OD2
即 R2 = 18.72 + (R-7.2)2 解得 R≈27.9
因此，赵州桥的主桥拱的半径约为27.9米。