





数学第二十一章 一元二次方程21.1 一元二次方程教课内容课件ppt
展开一元一次方程二元一次方程(组)分式方程数的开方二次根式
1、知道一元二次方程的定义,能熟练地把一元二次方程整理成一般形式(≠0),并能指出二次项系数、一次项系数和常数项。2、经历由实际问题抽象出一元二次方程和过程,进一步体会方程是刻画现实世界数量关系的一种有效数学模型,增加对一元二次方程的感性认识。3、在实际问题转化为数学模型( 一元二次方程 ) 的过程中,体会学习一元二次方程的必要性和重要性。
1、下列式子哪些是方程?
2+3=5 3x+2 5x+3=18x-2y=5
含有未知数的等式叫方程
方程的本质特征是什么?
2、我们学过哪些方程?
一元一次方程、二元一次方程、分式方程。
3、什么叫一元一次方程?方程的“元”和“次”是什么意思?
只含有一个未知数,并且未知数的次数是1次的整式方程叫一元一次方程。
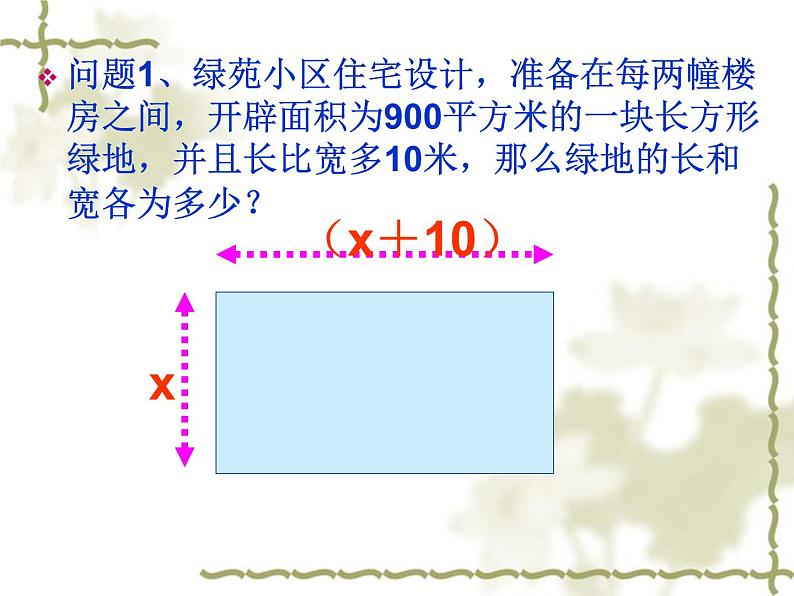
问题1、绿苑小区住宅设计,准备在每两幢楼房之间,开辟面积为900平方米的一块长方形绿地,并且长比宽多10米,那么绿地的长和宽各为多少?
解:设长方形绿地的宽为x米,则长为(x+10)米,可得方程:
长×宽=面积 相等关系
x(x+10)=900,
今年底:5+5x=5(1+x)
明年底:5(1+x)+5(1+x)x=5(1+x)(1+x)
问题2、学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册。求这两年的年平均增长率。
解:设这两年的年平均增长率为x,
根据题意得方程:5(1+x)2=7.2
注意:每年都是在上一年的基础上增长!
x2+10x-900=0 (1)
5x2+10x-2.2=0 (2)
特征(1) 都是整式方程 (2) 只含有一个未知数 (3) 未知数的最高次数是2
只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程通常可写成如下的一般形式:
ax2+bx+c=0(a≠0)
特征:方程的左边按x的降幂排列, 右边=0
练习:下列方程中哪些是一元二次方程?试说明理由。
讨论:为什么二次项系数a不能为0?假如a=0会出现什么情况?b、c能不能为0?
一元二次方程的项和各项系数
练习 1、指出下列一元二次方程的二次项系数、一次项系数和常数项:
2、将下列一元二次方程化为一般形式,并分别指出它们的二次项系数、一次项系数和常数项:
2x2-5x-11=0
友情提示:某一项的系数包括它前面的符号。
1、 关于x的方程ax2 —2bx+a=2x2, 在什么条件下此方程为一元二次方程?在什么条件下此方程为一元一次方程?
解:移项:ax2 —2bx+a- 2x2 =0
合并同类项:(a-2)x2 —2bx+a=0
所以,当a≠2时是一元二次方程;
当a=2,b≠0时是一元一次方程;
2、已知关于x的一元二次方程 (m-1)x2+3x-5m+4=0有一根为2,求m。
能够使方程左右两边相等的未知数的值,叫方程的根。
解:把x=2代入原方程得: (m-1) ×22+3 ×2 -5m+4=0解这个方程得:m=6
3、已知关于x的方程 是一元二次方程,求m的值。
分析:因为方程是一元二次方程,故未知数x的最高次数∣m∣+1=2,解之得,m=1或m=-1,又因二次项系数m+1≠0, 即m≠-1,所以m=1。
温馨提示:注意陷井二次项系数a≠0!
§26.1 二次函数y=ax2的图象和性质
1、二次函数的一般形式是怎样的?
y=ax²+bx+c(a,b,c是常数,a≠ 0)
你会用描点法画二次函数y=x2的图象吗?
观察y=x2的表达式,选择适当x值,并计算相应的y值,完成下表:
二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线
这条抛物线关于y轴对称,y轴就 是它的对称轴.
对称轴与抛物线的交点叫做抛物线的顶点.
(2)图象 与x轴有交点吗?如果有,交点坐标是什么?
(4)当x<0时,随着x的值增大,y 的值如何变化?当x>0呢?
(3)当x取什么值时,y的值最小?最小值是什么? 你是如何知道的?
(1)图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点?
当x<0 (在对称轴的左侧)时,y随着x的增大而减小.
当x>0 (在对称轴的右侧)时, y随着x的增大而增大.
抛物线y=x2在x轴的上方(除顶点外),顶点是它的最低点,开口向上,并且向上无限伸展;当x=0时,函数y的值最小,最小值是0.
(1)二次函数y=-x2的图象是什么形状?
你能根据表格中的数据作出猜想吗?
(2)先想一想,然后作出它的图象.
(3)它与二次函数y=x2的图象有什么关系?
当x<0 (在对称轴的左侧)时,y随着x的增大而增大.
当x>0 (在对称轴的右侧)时, y随着x的增大而减小.
抛物线y= -x2在x轴的下方(除顶点外),顶点是它的最高点,开口向下,并且向下无限伸展;当x=0时,函数y的值最大,最大值是0.
1.抛物线y=ax2的顶点是原点,对称轴是y轴.
2.当a>0时,抛物线y=ax2在x轴的上方(除顶点外),它的开口向上,并且向上无限伸展; 当a<0时,抛物线y=ax2在x轴的下方(除顶点外),它的开口向下,并且向下无限伸展.
3.当a>0时,在对称轴的左侧,y随着x的增大而减小;在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小. 当a<0时,在对称轴的左侧,y随着x的增大而增大;在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.
二次函数y=ax2的性质
(1)抛物线y=2x2的顶点坐标是 ,对称轴是 , 在对称轴 侧,y随着x的增大而增大;在对称轴 侧, y随着x的增大而减小,当x= 时,函数y的值最小,最小 值是 ,抛物线y=2x2在x轴的 方(除顶点外).
初中数学人教版九年级上册21.1 一元二次方程精品课件ppt: 这是一份初中数学人教版九年级上册21.1 一元二次方程精品课件ppt,文件包含211《一元二次方程》课件--人教版数学九上pptx、211《一元二次方程》教案--人教版数学九上docx等2份课件配套教学资源,其中PPT共16页, 欢迎下载使用。
初中数学人教版九年级上册21.1 一元二次方程精品课件ppt: 这是一份初中数学人教版九年级上册21.1 一元二次方程精品课件ppt,文件包含211《一元二次方程》课件--人教版数学九上pptx、211《一元二次方程》教案--人教版数学九上docx等2份课件配套教学资源,其中PPT共16页, 欢迎下载使用。
数学21.1 一元二次方程备课课件ppt: 这是一份数学21.1 一元二次方程备课课件ppt,共17页。PPT课件主要包含了一般形式,下列方程的根是什么等内容,欢迎下载使用。













