2020年江苏省镇江市中考数学试卷 解析版

2020年江苏省镇江市中考数学试卷
一、选择题（本大题共6小题，每小题3分，共18分．在每小题给出的四个选项中，只有一项是符合题目要求的）
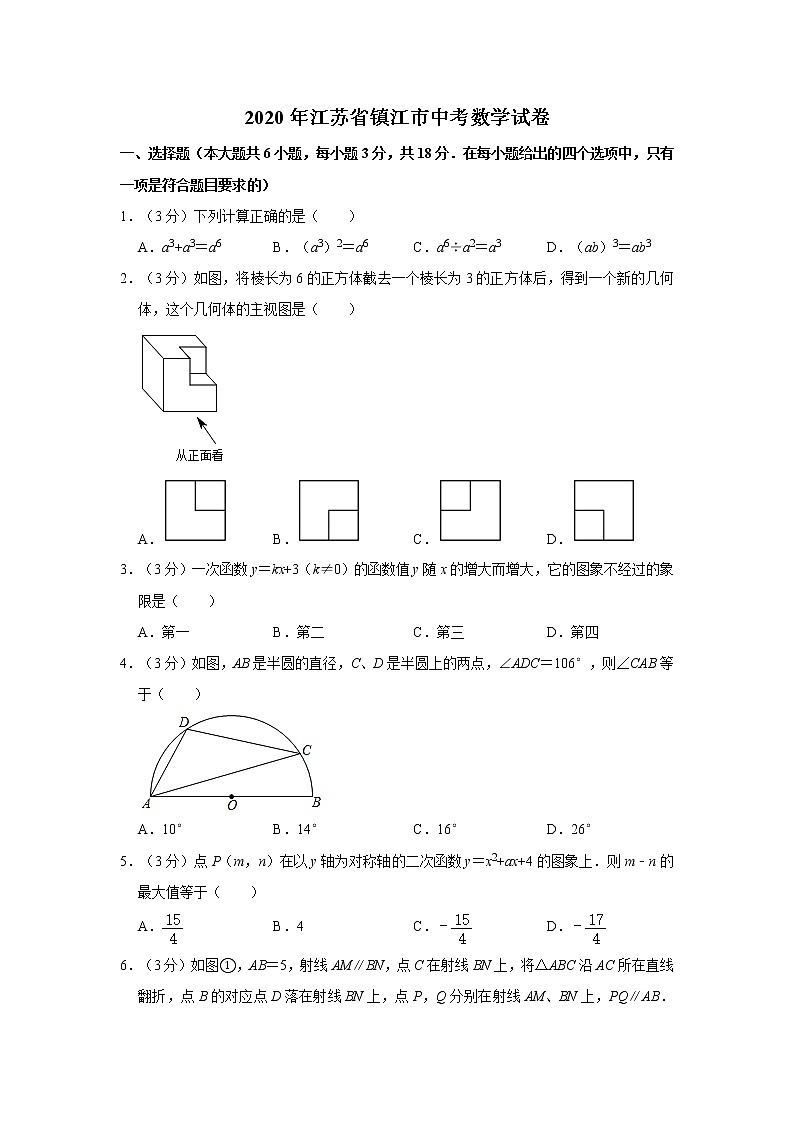
1．（3分）下列计算正确的是（　　）
A．a3+a3＝a6 B．（a3）2＝a6 C．a6÷a2＝a3 D．（ab）3＝ab3
2．（3分）如图，将棱长为6的正方体截去一个棱长为3的正方体后，得到一个新的几何体，这个几何体的主视图是（　　）

A． B． C． D．
3．（3分）一次函数y＝kx+3（k≠0）的函数值y随x的增大而增大，它的图象不经过的象限是（　　）
A．第一 B．第二 C．第三 D．第四
4．（3分）如图，AB是半圆的直径，C、D是半圆上的两点，∠ADC＝106°，则∠CAB等于（　　）

A．10° B．14° C．16° D．26°
5．（3分）点P（m，n）在以y轴为对称轴的二次函数y＝x2+ax+4的图象上．则m﹣n的最大值等于（　　）
A． B．4 C．﹣ D．﹣
6．（3分）如图①，AB＝5，射线AM∥BN，点C在射线BN上，将△ABC沿AC所在直线翻折，点B的对应点D落在射线BN上，点P，Q分别在射线AM、BN上，PQ∥AB．设AP＝x，QD＝y．若y关于x的函数图象（如图②）经过点E（9，2），则cosB的值等于（　　）

A． B． C． D．
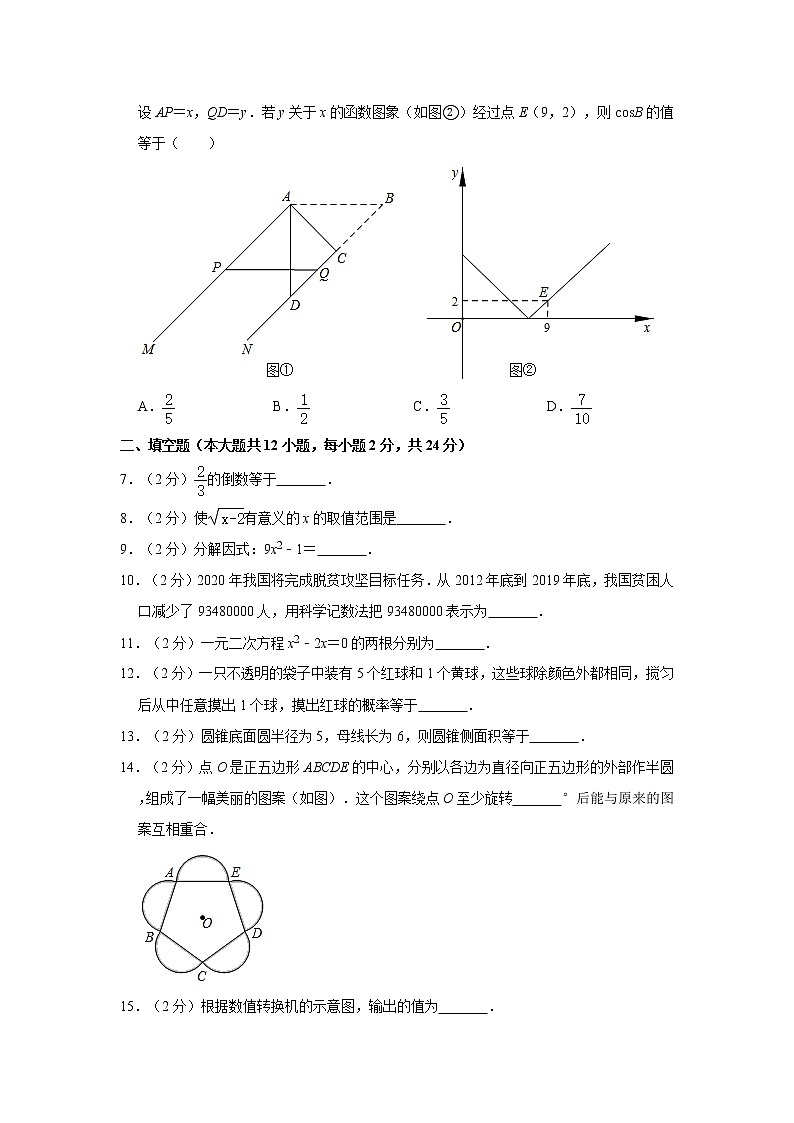
二、填空题（本大题共12小题，每小题2分，共24分）
7．（2分）的倒数等于　 　．
8．（2分）使有意义的x的取值范围是　 　．
9．（2分）分解因式：9x2﹣1＝　 　．
10．（2分）2020年我国将完成脱贫攻坚目标任务．从2012年底到2019年底，我国贫困人口减少了93480000人，用科学记数法把93480000表示为　 　．
11．（2分）一元二次方程x2﹣2x＝0的两根分别为　 　．
12．（2分）一只不透明的袋子中装有5个红球和1个黄球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，摸出红球的概率等于　 　．
13．（2分）圆锥底面圆半径为5，母线长为6，则圆锥侧面积等于　 　．
14．（2分）点O是正五边形ABCDE的中心，分别以各边为直径向正五边形的外部作半圆，组成了一幅美丽的图案（如图）．这个图案绕点O至少旋转　 　°后能与原来的图案互相重合．

15．（2分）根据数值转换机的示意图，输出的值为　 　．

16．（2分）如图，点P是正方形ABCD内位于对角线AC下方的一点，∠1＝∠2，则∠BPC的度数为　 　°．

17．（2分）在从小到大排列的五个数x，3，6，8，12中再加入一个数，若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等，则x的值为　 　．
18．（2分）如图，在△ABC中，BC＝3，将△ABC平移5个单位长度得到△A1B1C1，点P、Q分别是AB、A1C1的中点，PQ的最小值等于　 　．

三、解答题（本大题共10小题，共78分．解答时应写出必要的计算过程、推演步骤或文字说明）
19．（8分）（1）计算：4sin60°﹣+（﹣1）0；
（2）化简（x+1）÷（1+）．
20．（10分）（1）解方程：＝+1；
（2）解不等式组：
21．（6分）如图，AC是四边形ABCD的对角线，∠1＝∠B，点E、F分别在AB、BC上，BE＝CD，BF＝CA，连接EF．
（1）求证：∠D＝∠2；
（2）若EF∥AC，∠D＝78°，求∠BAC的度数．

22．（6分）教育部发布的义务教育质量监测结果报告显示，我国八年级学生平均每天的睡眠时间达9小时及以上的比例为19.4%．某校数学社团成员采用简单随机抽样的方法，抽取了本校八年级50名学生，对他们一周内平均每天的睡眠时间t（单位：小时）进行了调查，将数据整理后绘制成下表：
平均每天的睡眠时间分组
5≤t＜6
6≤t＜7
7≤t＜8
8≤t＜9
9小时及以上
频数
1
5
m
24
n
该样本中学生平均每天的睡眠时间达9小时及以上的比例高于全国的这项数据，达到了22%．
（1）求表格中n的值；
（2）该校八年级共400名学生，估计其中平均每天的睡眠时间在7≤t＜8这个范围内的人数是多少．
23．（6分）智慧的中国古代先民发明了抽象的符号来表达丰富的含义．例如，符号“”有刚毅的含义，符号“”有愉快的含义．符号中的“”表示“阴”，“”表示“阳”，类似这样自上而下排成的三行符号还有其他的含义．所有这些三行符号中，每一行只有一个阴或一个阳，且出现阴、阳的可能性相同．
（1）所有这些三行符号共有　 　种；
（2）若随机画一个这样的三行符号，求“画出含有一个阴和两个阳的三行符号”的概率．
24．（6分）如图，点E与树AB的根部点A、建筑物CD的底部点C在一条直线上，AC＝10m．小明站在点E处观测树顶B的仰角为30°，他从点E出发沿EC方向前进6m到点G时，观测树顶B的仰角为45°，此时恰好看不到建筑物CD的顶部D（H、B、D三点在一条直线上）．已知小明的眼睛离地面1.6m，求建筑物CD的高度（结果精确到0.1m）．（参考数据：≈1.41，≈1.73．）

25．（6分）如图，正比例函数y＝kx（k≠0）的图象与反比例函数y＝﹣的图象交于点A（n，2）和点B．
（1）n＝　 　，k＝　 　；
（2）点C在y轴正半轴上．∠ACB＝90°，求点C的坐标；
（3）点P（m，0）在x轴上，∠APB为锐角，直接写出m的取值范围．

26．（8分）如图，▱ABCD中，∠ABC的平分线BO交边AD于点O，OD＝4，以点O为圆心，OD长为半径作⊙O，分别交边DA、DC于点M、N．点E在边BC上，OE交⊙O于点G，G为的中点．
（1）求证：四边形ABEO为菱形；
（2）已知cos∠ABC＝，连接AE，当AE与⊙O相切时，求AB的长．

27．（11分）【算一算】
如图①，点A、B、C在数轴上，B为AC的中点，点A表示﹣3，点B表示1，则点C表示的数为　 　，AC长等于　 　；
【找一找】
如图②，点M、N、P、Q中的一点是数轴的原点，点A、B分别表示实数﹣1、+1，Q是AB的中点，则点　 　是这个数轴的原点；
【画一画】
如图③，点A、B分别表示实数c﹣n、c+n，在这个数轴上作出表示实数n的点E（要求：尺规作图，不写作法，保留作图痕迹）；
【用一用】
学校设置了若干个测温通道，学生进校都应测量体温，已知每个测温通道每分钟可检测a个学生．凌老师提出了这样的问题：假设现在校门口有m个学生，每分钟又有b个学生到达校门口．如果开放3个通道，那么用4分钟可使校门口的学生全部进校；如果开放4个通道，那么用2分钟可使校门口的学生全部进校．在这些条件下，a、m、b会有怎样的数量关系呢？
爱思考的小华想到了数轴，如图④，他将4分钟内需要进校的人数m+4b记作+（m+4b），用点A表示；将2分钟内由4个开放通道检测后进校的人数，即校门口减少的人数8a记作﹣8a，用点B表示．
①用圆规在小华画的数轴上分别画出表示+（m+2b）、﹣12a的点F、G，并写出+（m+2b）的实际意义；
②写出a、m的数量关系：　 　．

28．（11分）如图①，直线l经过点（4，0）且平行于y轴，二次函数y＝ax2﹣2ax+c（a、c是常数，a＜0）的图象经过点M（﹣1，1），交直线l于点N，图象的顶点为D，它的对称轴与x轴交于点C，直线DM、DN分别与x轴相交于A、B两点．
（1）当a＝﹣1时，求点N的坐标及的值；
（2）随着a的变化，的值是否发生变化？请说明理由；
（3）如图②，E是x轴上位于点B右侧的点，BC＝2BE，DE交抛物线于点F．若FB＝FE，求此时的二次函数表达式．


2020年江苏省镇江市中考数学试卷
参考答案与试题解析
一、选择题（本大题共6小题，每小题3分，共18分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1．（3分）下列计算正确的是（　　）
A．a3+a3＝a6 B．（a3）2＝a6 C．a6÷a2＝a3 D．（ab）3＝ab3
【分析】根据同底数幂的乘除法、幂的乘方的计算法则进行计算即可．
【解答】解：a3+a3＝2a3，因此选项A不正确；
（a3）2＝a3×2＝a6，因此选项B正确；
a6÷a2＝a6﹣2＝m4，因此选项C不正确；
（ab）3＝a3b3，因此选项D不正确；
故选：B．
2．（3分）如图，将棱长为6的正方体截去一个棱长为3的正方体后，得到一个新的几何体，这个几何体的主视图是（　　）

A． B． C． D．
【分析】根据从正面看得到的视图是主视图，可得答案．
【解答】解：从正面看是一个正方形，正方形的右上角是一个小正方形，
故选：A．
3．（3分）一次函数y＝kx+3（k≠0）的函数值y随x的增大而增大，它的图象不经过的象限是（　　）
A．第一 B．第二 C．第三 D．第四
【分析】根据一次函数y＝kx+3（k≠0）的函数值y随x的增大而增大，可以得到k＞0，与y轴的交点为（0，3），然后根据一次函数的性质，即可得到该函数图象经过哪几个象限，不经过哪个象限，从而可以解答本题．
【解答】解：∵一次函数y＝kx+3（k≠0）的函数值y随x的增大而增大，
∴k＞0，该函数过点（0，3），
∴该函数的图象经过第一、二、三象限，不经过第四象限，
故选：D．
4．（3分）如图，AB是半圆的直径，C、D是半圆上的两点，∠ADC＝106°，则∠CAB等于（　　）

A．10° B．14° C．16° D．26°
【分析】连接BD，如图，根据圆周角定理得到∠ADB＝90°，则可计算出∠BDC＝16°，然后根据圆周角定理得到∠CAB的度数．
【解答】解：连接BD，如图，
∵AB是半圆的直径，
∴∠ADB＝90°，
∴∠BDC＝∠ADC﹣∠ADB＝106°﹣90°＝16°，
∴∠CAB＝∠BDC＝16°．
故选：C．

5．（3分）点P（m，n）在以y轴为对称轴的二次函数y＝x2+ax+4的图象上．则m﹣n的最大值等于（　　）
A． B．4 C．﹣ D．﹣
【分析】根据题意，可以得到a的值，m和n的关系，然后将m、n作差，利用二次函数的性质，即可得到m﹣n的最大值，本题得以解决．
【解答】解：∵点P（m，n）在以y轴为对称轴的二次函数y＝x2+ax+4的图象上，
∴a＝0，
∴n＝m2+4，
∴m﹣n＝m﹣（m2+4）＝﹣m2+m﹣4＝﹣（m﹣）2﹣，
∴当m＝时，m﹣n取得最大值，此时m﹣n＝﹣，
故选：C．
6．（3分）如图①，AB＝5，射线AM∥BN，点C在射线BN上，将△ABC沿AC所在直线翻折，点B的对应点D落在射线BN上，点P，Q分别在射线AM、BN上，PQ∥AB．设AP＝x，QD＝y．若y关于x的函数图象（如图②）经过点E（9，2），则cosB的值等于（　　）

A． B． C． D．
【分析】由题意可得四边形ABQP是平行四边形，可得AP＝BQ＝x，由图象②可得当x＝9时，y＝2，此时点Q在点D下方，且BQ＝x＝9时，y＝2，如图①所示，可求BD＝7，由折叠的性质可求BC的长，由锐角三角函数可求解．
【解答】解：∵AM∥BN，PQ∥AB，
∴四边形ABQP是平行四边形，
∴AP＝BQ＝x，
由图②可得当x＝9时，y＝2，
此时点Q在点D下方，且BQ＝x＝9时，y＝2，如图①所示，

∴BD＝BQ﹣QD＝x﹣y＝7，
∵将△ABC沿AC所在直线翻折，点B的对应点D落在射线BN上，
∴BC＝CD＝BD＝，AC⊥BD，
∴cosB＝＝＝，
故选：D．
二、填空题（本大题共12小题，每小题2分，共24分）
7．（2分）的倒数等于　　．
【分析】根据倒数的意义求解即可．
【解答】解：∵×＝1，
∴的倒数是，
故答案为：．
8．（2分）使有意义的x的取值范围是　x≥2　．
【分析】当被开方数x﹣2为非负数时，二次根式才有意义，列不等式求解．
【解答】解：根据二次根式的意义，得
x﹣2≥0，解得x≥2．
9．（2分）分解因式：9x2﹣1＝　（3x+1）（3x﹣1）　．
【分析】符合平方差公式的结构特点，利用平方差公式分解即可．
【解答】解：9x2﹣1，
＝（3x）2﹣12，
＝（3x+1）（3x﹣1）．
10．（2分）2020年我国将完成脱贫攻坚目标任务．从2012年底到2019年底，我国贫困人口减少了93480000人，用科学记数法把93480000表示为　9.348×107　．
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值是易错点，由于93480000有8位，所以可以确定n＝8﹣1＝7．
【解答】解：93480000＝9.348×107．
故答案为：9.348×107．
11．（2分）一元二次方程x2﹣2x＝0的两根分别为　x1＝0，x2＝2　．
【分析】利用因式分解法求解可得．
【解答】解：∵x2﹣2x＝0，
∴x（x﹣2）＝0，
∴x＝0或x﹣2＝0，
解得x1＝0，x2＝2．
12．（2分）一只不透明的袋子中装有5个红球和1个黄球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，摸出红球的概率等于　　．
【分析】用红球的个数除以球的总个数即可得．
【解答】解：∵袋子中共有5+1＝6个小球，其中红球有5个，
∴搅匀后从中任意摸出1个球，摸出红球的概率等于，
故答案为：．
13．（2分）圆锥底面圆半径为5，母线长为6，则圆锥侧面积等于　30π　．
【分析】利用扇形的面积公式计算圆锥侧面积．
【解答】解：圆锥侧面积＝×2π×5×6＝30π．
故答案为30π．
14．（2分）点O是正五边形ABCDE的中心，分别以各边为直径向正五边形的外部作半圆，组成了一幅美丽的图案（如图）．这个图案绕点O至少旋转　72　°后能与原来的图案互相重合．

【分析】直接利用旋转图形的性质进而得出旋转角．
【解答】解：连接OA，OE，则这个图形至少旋转∠AOE才能与原图象重合，
∠AOE＝＝72°．
故答案为：72．
15．（2分）根据数值转换机的示意图，输出的值为　　．

【分析】利用代入法和负整数指数幂的计算方法进行计算即可．
【解答】解：当x＝﹣3时，31+x＝3﹣2＝，
故答案为：．
16．（2分）如图，点P是正方形ABCD内位于对角线AC下方的一点，∠1＝∠2，则∠BPC的度数为　135　°．

【分析】由正方形的性质可得∠ACB＝∠BAC＝45°，可得∠2+∠BCP＝45°＝∠1+∠BCP，由三角形内角和定理可求解．
【解答】解：∵四边形ABCD是正方形，
∴∠ACB＝∠BAC＝45°，
∴∠2+∠BCP＝45°，
∵∠1＝∠2，
∴∠1+∠BCP＝45°，
∵∠BPC＝180°﹣∠1﹣∠BCP，
∴∠BPC＝135°，
故答案为：135．
17．（2分）在从小到大排列的五个数x，3，6，8，12中再加入一个数，若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等，则x的值为　1　．
【分析】原来五个数的中位数是6，如果再加入一个数，变成了偶数个数，则中位数是中间两位数的平均数，由此可知加入的一个数是6，再根据平均数的公式得到关于x的方程，解方程即可求解．
【解答】解：从小到大排列的五个数x，3，6，8，12的中位数是6，
∵再加入一个数，这六个数的中位数与原来五个数的中位数相等，
∴加入的一个数是6，
∵这六个数的平均数与原来五个数的平均数相等，
∴（x+3+6+8+12）＝（x+3+6+6+8+12），
解得x＝1．
故答案为：1．
18．（2分）如图，在△ABC中，BC＝3，将△ABC平移5个单位长度得到△A1B1C1，点P、Q分别是AB、A1C1的中点，PQ的最小值等于　　．

【分析】取AC的中点M，A1B1的中点N，连接PM，MQ，NQ，PN，根据平移的性质和三角形的三边关系即可得到结论．
【解答】解：取AC的中点M，A1B1的中点N，连接PM，MQ，NQ，PN，
∵将△ABC平移5个单位长度得到△A1B1C1，
∴B1C1＝BC＝3，PN＝5，
∵点P、Q分别是AB、A1C1的中点，
∴NQ＝B1C1＝，
∴5﹣≤PQ≤5+，
即≤PQ≤，
∴PQ的最小值等于，
故答案为：．

三、解答题（本大题共10小题，共78分．解答时应写出必要的计算过程、推演步骤或文字说明）
19．（8分）（1）计算：4sin60°﹣+（﹣1）0；
（2）化简（x+1）÷（1+）．
【分析】（1）先代入三角函数值、化简二次根式、计算零指数幂，再计算乘法，最后计算加减可得；
（2）先计算括号内分式的加法，再将除法转化为乘法，最后约分即可得．
【解答】解：（1）原式＝4×﹣2+1
＝2﹣2+1
＝1；

（2）原式＝（x+1）÷（+）
＝（x+1）÷
＝（x+1）•
＝x．
20．（10分）（1）解方程：＝+1；
（2）解不等式组：
【分析】（1）解分式方程的步骤有：去分母，去括号，移项，合并同类项，系数化为1，检验；
（2）先求出每个不等式的解集，再在数轴上表示出其解集，然后根据是否存在公共部分求解即可．
【解答】解：（1）＝+1，
2x＝1+x+3，
2x﹣x＝1+3，
x＝4，
经检验，x＝4是原方程的解，
∴此方程的解是x＝4；

（2），
①4x﹣x＞﹣2﹣7，
3x＞﹣9，
x＞﹣3；
②3x﹣6＜4+x，
3x﹣x＜4+6，
2x＜10，
x＜5，

∴不等式组的解集是﹣3＜x＜5．
21．（6分）如图，AC是四边形ABCD的对角线，∠1＝∠B，点E、F分别在AB、BC上，BE＝CD，BF＝CA，连接EF．
（1）求证：∠D＝∠2；
（2）若EF∥AC，∠D＝78°，求∠BAC的度数．

【分析】（1）由“SAS”可证△BEF≌△CDA，可得∠D＝∠2；
（2）由（1）可得∠D＝∠2＝78°，由平行线的性质可得∠2＝∠BAC＝78°．
【解答】证明：（1）在△BEF和△CDA中，
，
∴△BEF≌△CDA（SAS），
∴∠D＝∠2；
（2）∵∠D＝∠2，∠D＝78°，
∴∠D＝∠2＝78°，
∵EF∥AC，
∴∠2＝∠BAC＝78°．
22．（6分）教育部发布的义务教育质量监测结果报告显示，我国八年级学生平均每天的睡眠时间达9小时及以上的比例为19.4%．某校数学社团成员采用简单随机抽样的方法，抽取了本校八年级50名学生，对他们一周内平均每天的睡眠时间t（单位：小时）进行了调查，将数据整理后绘制成下表：
平均每天的睡眠时间分组
5≤t＜6
6≤t＜7
7≤t＜8
8≤t＜9
9小时及以上
频数
1
5
m
24
n
该样本中学生平均每天的睡眠时间达9小时及以上的比例高于全国的这项数据，达到了22%．
（1）求表格中n的值；
（2）该校八年级共400名学生，估计其中平均每天的睡眠时间在7≤t＜8这个范围内的人数是多少．
【分析】（1）根据频率＝求解可得；
（2）先根据频数的和是50及n的值求出m的值，再用总人数乘以样本中平均每天的睡眠时间在7≤t＜8这个范围内的人数所占比例即可得．
【解答】解：（1）n＝50×22%＝11；
（2）m＝50﹣1﹣5﹣24﹣11＝9，
所以估计该校平均每天的睡眠时间在7≤t＜8这个范围内的人数是400×＝72（人）．
23．（6分）智慧的中国古代先民发明了抽象的符号来表达丰富的含义．例如，符号“”有刚毅的含义，符号“”有愉快的含义．符号中的“”表示“阴”，“”表示“阳”，类似这样自上而下排成的三行符号还有其他的含义．所有这些三行符号中，每一行只有一个阴或一个阳，且出现阴、阳的可能性相同．
（1）所有这些三行符号共有　8　种；
（2）若随机画一个这样的三行符号，求“画出含有一个阴和两个阳的三行符号”的概率．
【分析】（1）用列举法举出所有等可能的结果数即可；
（2）根据（1）列举的结果数和概率公式即可得出答案．
【解答】解：（1）共有8种等可能的情况数，分别是：阴，阴，阴；阴，阳，阴；阴，阴，阳；阳，阴，阴；阳，阳，阴；阳，阴，阳；阴，阳，阳；阳、阳、阳；
故答案为：8；

（2）根据第（1）问一个阴、两个阳的共有3种，
则有一个阴和两个阳的三行符号”的概率是．
24．（6分）如图，点E与树AB的根部点A、建筑物CD的底部点C在一条直线上，AC＝10m．小明站在点E处观测树顶B的仰角为30°，他从点E出发沿EC方向前进6m到点G时，观测树顶B的仰角为45°，此时恰好看不到建筑物CD的顶部D（H、B、D三点在一条直线上）．已知小明的眼睛离地面1.6m，求建筑物CD的高度（结果精确到0.1m）．（参考数据：≈1.41，≈1.73．）

【分析】延长FH，交CD于点M，交AB于点N，求CD，只需求出DM即可，即只要求出HN就可以，在Rt△BNF中，设BN＝NH＝x，则根据tan∠BFN＝就可以求出x的值，再根据等腰直角三角形的性质和线段的和可求得CD的长．
【解答】解：如图，延长FH，交CD于点M，交AB于点N，

∵∠BHN＝45°，BA⊥MH，
则BN＝NH，
设BN＝NH＝x，
∵HF＝6，∠BFN＝30°，
∴tan∠BFN＝＝，
即tan30°＝，
解得x＝8.19，
根据题意可知：
DM＝MH＝MN+NH，
∵MN＝AC＝10，
则DM＝10+8.19＝18.19，
∴CD＝DM+MC＝DM+EF＝18.19+1.6＝19.79≈19.8（m）．
答：建筑物CD的高度约为19.8m．
25．（6分）如图，正比例函数y＝kx（k≠0）的图象与反比例函数y＝﹣的图象交于点A（n，2）和点B．
（1）n＝　﹣4　，k＝　﹣　；
（2）点C在y轴正半轴上．∠ACB＝90°，求点C的坐标；
（3）点P（m，0）在x轴上，∠APB为锐角，直接写出m的取值范围．

【分析】（1）把A点坐标代入反比例函数解析式求得n，再把求得的A点坐标代入正比例函数解析式求得k；
（2）可设点C（0，b），只要求出b的值就行，求值一般的方法是相似和勾股定理，此题用相似，只需证明△ACD∽△CBE即可；
（3）在x轴上找到点P1，P2，使AP1⊥P1B，AP2⊥BP2，则点P在P1的左边，在P2的右边就符合要求了．
【解答】解：（1）把A（n，2）代入反比例函数y＝﹣中，得n＝﹣4，
∴A（﹣4，2），
把A（﹣4，2）代入正比例函数y＝kx（k≠0）中，得k＝﹣，
故答案为：﹣4；﹣；
（2）过A作AD⊥y轴于D，过B作BE⊥y轴于E，

∵A（﹣4，2），
∴根据双曲线与正比例函数图象的对称性得B（4，﹣2），
设C（0，b），则CD＝b﹣2，AD＝4，BE＝E，CE＝b+2，
∵∠ACO+∠OCB＝90°，∠OCB+∠CBE＝90°，
∴∠ACO＝∠CBE，
∵∠ADC＝∠CEB＝90°，
∴△ACD∽△CBE，
∴，即，
解得，b＝2，或b＝﹣2（舍），
∴C（0，2）；
（3）如图2，过A作AM⊥x轴于M，过B作BN⊥x轴于N，在x轴上原点的两旁取两点P1，P2，使得OP1＝OP2＝OA＝OB，
∴，
∴P1（﹣2，0），P2（2，0），
∵OP1＝OP2＝OA＝OB，
∴四边形AP1BP2为矩形，
∴AP1⊥P1B，AP2⊥BP2，
∵点P（m，0）在x轴上，∠APB为锐角，
∴P点必在P1的左边或P2的右边，
∴m＜﹣2或m＞2．

26．（8分）如图，▱ABCD中，∠ABC的平分线BO交边AD于点O，OD＝4，以点O为圆心，OD长为半径作⊙O，分别交边DA、DC于点M、N．点E在边BC上，OE交⊙O于点G，G为的中点．
（1）求证：四边形ABEO为菱形；
（2）已知cos∠ABC＝，连接AE，当AE与⊙O相切时，求AB的长．

【分析】（1）先由G为的中点及同弧所对的圆周角和圆心角的关系得出∠MOG＝∠MDN，再由平行四边形的性质得出AO∥BE，∠MDN+∠A＝180°，进而判定四边形ABEO是平行四边形，然后证明AB＝AO，则可得结论；
（2）过点O作OP⊥BA，交BA的延长线于点P，过点O作OQ⊥BC于点Q，设AB＝AO＝OE＝x，则由cos∠ABC＝，可用含x的式子分别表示出PA、OP及OQ，由勾股定理得关于x的方程，解得x的值即可．
【解答】解：（1）证明：∵G为的中点，
∴∠MOG＝∠MDN．
∵四边形ABCD是平行四边形．
∴AO∥BE，∠MDN+∠A＝180°，
∴∠MOG+∠A＝180°，
∴AB∥OE，
∴四边形ABEO是平行四边形．
∵BO平分∠ABE，
∴∠ABO＝∠OBE，
又∵∠OBE＝∠AOB，
∴∠ABO＝∠AOB，
∴AB＝AO，
∴四边形ABEO为菱形；
（2）如图，过点O作OP⊥BA，交BA的延长线于点P，过点O作OQ⊥BC于点Q，设AE交OB于点F，

则∠PAO＝∠ABC，
设AB＝AO＝OE＝x，则
∵cos∠ABC＝，
∴cos∠PAO＝，
∴＝，
∴PA＝x，
∴OP＝OQ＝x
当AE与⊙O相切时，由菱形的对角线互相垂直，可知F为切点，
∴由勾股定理得：+＝82，
解得：x＝2．
∴AB的长为2．
27．（11分）【算一算】
如图①，点A、B、C在数轴上，B为AC的中点，点A表示﹣3，点B表示1，则点C表示的数为　5　，AC长等于　8　；
【找一找】
如图②，点M、N、P、Q中的一点是数轴的原点，点A、B分别表示实数﹣1、+1，Q是AB的中点，则点　N　是这个数轴的原点；
【画一画】
如图③，点A、B分别表示实数c﹣n、c+n，在这个数轴上作出表示实数n的点E（要求：尺规作图，不写作法，保留作图痕迹）；
【用一用】
学校设置了若干个测温通道，学生进校都应测量体温，已知每个测温通道每分钟可检测a个学生．凌老师提出了这样的问题：假设现在校门口有m个学生，每分钟又有b个学生到达校门口．如果开放3个通道，那么用4分钟可使校门口的学生全部进校；如果开放4个通道，那么用2分钟可使校门口的学生全部进校．在这些条件下，a、m、b会有怎样的数量关系呢？
爱思考的小华想到了数轴，如图④，他将4分钟内需要进校的人数m+4b记作+（m+4b），用点A表示；将2分钟内由4个开放通道检测后进校的人数，即校门口减少的人数8a记作﹣8a，用点B表示．
①用圆规在小华画的数轴上分别画出表示+（m+2b）、﹣12a的点F、G，并写出+（m+2b）的实际意义；
②写出a、m的数量关系：　m＝4a　．

【分析】（1）根据数轴上点A对应﹣3，点B对应1，求得AB的长，进而根据AB＝BC可求得AC的长以及点C表示的数；
（2）可设原点为O，根据条件可求得AB中点表示的数以及线段AB的长度，根据AB＝2，可得AQ＝BQ＝1，结合OQ的长度即可确定N为数轴的原点；
（3）设AB的中点为M，先求得AB的长度，得到AM＝BM＝n，根据线段垂直平分线的作法作图即可；
（4）①根据每分钟进校人数为b，每个通道每分钟进入人数为a，列方程组，根据m+2b＝OF，m+4b＝12a，即可画出F，G点，其中m+2b表示两分钟后，校门口需要进入学校的学生人数；
②解①中的方程组，即可得到m＝4a．
【解答】解：（1）【算一算】：记原点为O，
∵AB＝1﹣（﹣3）＝4，
∴AB＝BC＝4，
∴OC＝OB+BC＝5，AC＝2AB＝8．
所以点C表示的数为5，AC长等于8．
故答案为：5，8；
（2）【找一找】：记原点为O，
∵AB＝+1﹣（﹣1）＝2，
∴AQ＝BQ＝1，
∴OQ＝OB﹣BQ＝+1﹣1＝，
∴N为原点．
故答案为：N．
（3）【画一画】：记原点为O，
由AB＝c+n﹣（c﹣n）＝2n，
作AB的中点M，
得AM＝BM＝n，
以点O为圆心，
AM＝n长为半径作弧交数轴的正半轴于点E，
则点E即为所求；

（4）【用一用】：在数轴上画出点F，G；2分钟后，校门口需要进入学校的学生人数为：m＝4a．
∵4分钟内开放3个通道可使学生全部进校，
∴m+4b＝3×a×4，即m+4b＝12a（Ⅰ）；
∵2分钟内开放4个通道可使学生全部进校，
∴m+2b＝4×a×2，即m+2b＝8a（Ⅱ）；
①以O为圆心，OB长为半径作弧交数轴的正半轴于点F，则点F即为所求．
作OB的中点E，则OE＝BE＝4a，在数轴负半轴上用圆规截取OG＝3OE＝12a，
则点G即为所求．

+（m+2b）的实际意义：2分钟后，校门口需要进入学校的学生人数；
②方程（Ⅱ）×2﹣方程（Ⅰ）得：m＝4a．
故答案为：m＝4a．
28．（11分）如图①，直线l经过点（4，0）且平行于y轴，二次函数y＝ax2﹣2ax+c（a、c是常数，a＜0）的图象经过点M（﹣1，1），交直线l于点N，图象的顶点为D，它的对称轴与x轴交于点C，直线DM、DN分别与x轴相交于A、B两点．
（1）当a＝﹣1时，求点N的坐标及的值；
（2）随着a的变化，的值是否发生变化？请说明理由；
（3）如图②，E是x轴上位于点B右侧的点，BC＝2BE，DE交抛物线于点F．若FB＝FE，求此时的二次函数表达式．

【分析】（1）证明△DME∽△DAC，△DCB∽△DFN，则，，求出AC＝，BC＝，即可求解；
（2）点D（1，1﹣4a），N（4，1+5a），则ME＝2，DE＝﹣4a，由（1）的结论得：AC＝，BC＝，即可求解；
（3）利用△FHE∽△DCE，求出F（﹣，﹣a），即可求解．
【解答】解：（1）分别过点M、N作ME⊥CD于点E，NF⊥DC于点F，
∵ME∥FN∥x轴，

∴△DME∽△DAC，△DCB∽△DFN，
∴，，
∵a＝﹣1，则y＝﹣x2+2x+c，
将M（﹣1，1）代入上式并解得：c＝4，
∴抛物线的表达式为：y＝﹣x2+2x+4，
则点D（1，5），N（4，﹣4），
则ME＝2，DE＝4，DC＝5，FN＝3，DF＝9，
∴，解得：AC＝，BC＝，
∴＝；

（2）不变，理由：
∵y＝ax2﹣2ax+c过点M（﹣1，1），则a+2a+c＝1，
解得：c＝1﹣2a，
∴y＝ax2﹣2ax+（1﹣3a），
∴点D（1，1﹣4a），N（4，1+5a），
∴ME＝2，DE＝﹣4a，
由（1）的结论得：AC＝，BC＝，
∴＝；

（3）过点F作FH⊥x轴于点H，则FH∥l，则△FHE∽△DCE，

∵FB＝FE，FH⊥BE，
∴BH＝HE，
∵BC＝2BE，
则CE＝6HE，
∵CD＝1﹣4a，
∴FH＝，
∵BC＝，
∴CH＝×＝，
∴F（﹣，﹣a），
将点F的坐标代入y＝ax2﹣2ax+（1﹣3a）＝a（x+1）（x﹣3）+1得：
﹣a＝a（﹣+1）（﹣﹣3）+1，
解得：a＝﹣或﹣，
故y＝﹣x2+x+或y＝﹣x2+x+．