

2019届二轮复习求点的轨迹方程、求圆锥曲线方程学案(全国通用)
展开
考纲要求:
1.掌握椭圆、抛物线的定义、几何图形、标准方程及简单性质.
2.了解双曲线的定义、几何图形和标准方程,知道它的简单几何性质.
3.了解圆锥曲线的简单应用.
4.理解数形结合的思想.
5.了解方程的曲线与曲线的方程的对应关系.
基础知识回顾:
1、椭圆的标准方程和几何性质
条件 | ||
图形 | ||
标准方程 | ||
范围 | 学 ] | |
对称性 | 曲线关于轴、原点对称 | 曲线关于轴、原点对称 |
顶点 | 长轴顶点 ,短轴顶点 | |k ] | 长轴顶点 ,轴顶点 |
焦点 | ||
焦距 | 学 ] | |
离心率 | ,其中 | |
通径 | 过焦点垂直于长轴的弦叫通径,其长为 | |
椭圆离心率e与a,b的关系:e2=⇒=.
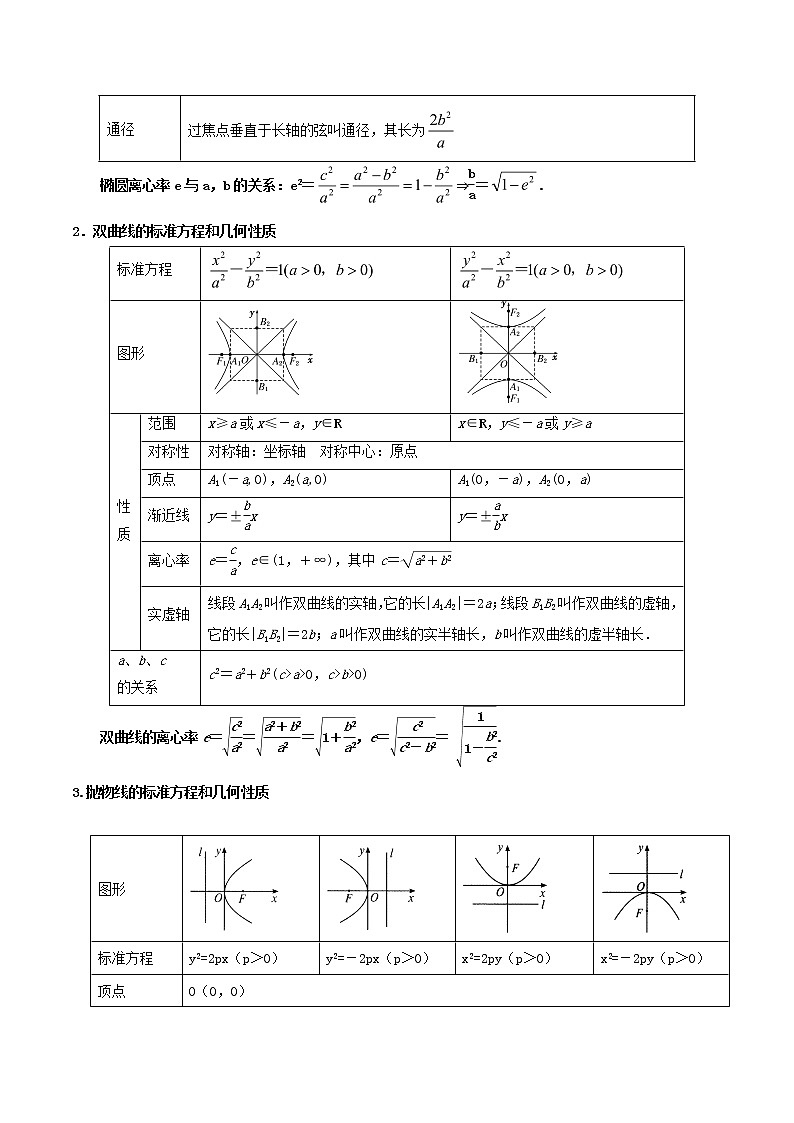
2.双曲线的标准方程和几何性质
标准方程 | |||
图形 | |||
性质 | |X|X|K] 学 ] 学 ] | 范围 | x≥a或x≤-a,y∈R ] | x∈R,y≤-a或y≥a 学 ] 学 ] |
对称性 | 对称轴:坐标轴 对称中心:原点 | ||
顶点 | A1(-a,0),A2(a,0) | A1(0,-a),A2(0,a) | |
渐近线 | y=±x | y=±x | |
离心率 | e=,e∈(1,+∞),其中c= | ||
实虚轴 | 线段A1A2叫作双曲线的实轴,它的长|A1A2|=2a;线段B1B2叫作双曲线的虚轴,它的长|B1B2|=2b;a叫作双曲线的实半轴长,b叫作双曲线的虚半轴长. | ||
a、b、c 的关系 | c2=a2+b2(c>a>0,c>b>0) | ||
双曲线的离心率e===,e== .
3.抛物线的标准方程和几何性质
图形 | ||||
标准方程 | y2=2px(p>0) | y2=-2px(p>0) | x2=2py(p>0) | x2=-2py(p>0) |
顶点 | O(0,0) | |||
范围 | x≥0, | x≤0, | y≥0, | y≤0, |
对称轴 | x轴 | y轴 | ||
焦点 | ||||
离心率 | e=1 | |||
准线方程 | ||||
焦半径 | ||||
4. 曲线与方程
在平面直角坐标系中,如果某曲线C(看作满足某种条件的点的集合或轨迹)上的点与一个二元方程的实数解建立了如下的关系:
(1)曲线上点的坐标都是这个方程的解;
(2)以这个方程的解为坐标的点都在曲线上.
那么,这个方程叫做曲线的方程;这条曲线叫做方程的曲线.
应用举例:
类型一、求点的轨迹方程
【例1】【湖南省衡阳市2017届高三下学期第三次联考】对任意平面向量,把绕其起点沿逆时针方向旋转角得到向量,叫做把点绕点逆时针方向旋转角得到点.设平面内曲线上的每一点绕原点沿逆时针方向旋转后得到点的轨迹是曲线
,则原来曲线的方程是( )
A. B. C. D.
【答案】A
【解析】设平面内曲线上的点,则其绕原点沿逆时针方向旋转后得到点
,∵点在曲线上,∴,整理得 .故选A.
【例2】【广东省中山市第一中学2019届高三入门考试】中,,给出满足的条件,就能得到动点的轨迹方程,下表给出了一些条件及方程:
条件 | 方程 |
① 周长为 | |
②面积为 | |
③中, |
则满足条件①,②,③的轨迹方程依次为
A. B. C. D.
【答案】B
【解析】试题分析:①中可转化为A点到B、C两点距离之和为常数,符合椭圆的定义,利用定义法求轨迹方程;②中利用三角形面积公式可知A点到BC距离为常数,轨迹为两条直线;③中∠A=90°,可用斜率或向量处理.
点睛:这道题目圆锥曲线中的求轨迹方程的方法;常见的方法有:数形结合法即几何法;相关点法,直接法;定义法,代入法,引入参数再消参的方法,交轨法是一种解决两直线交点的轨迹的方法,也是一种消参的方法.
【例3】【广西2018届高三下学期第二次模拟】为椭圆上任意一点,,,延长至点,使得,则点的轨迹方程为( )
A. B. C. D.
【答案】B
【解析】 为椭圆上任意一点,且A,B为焦点, ,又,,所以点的轨迹方程为.
点晴:求点的轨迹方程的基本步骤是:①建立适当的平面直角坐标系,设P(x,y)是轨迹上的任意一点;②寻找动点P(x,y)所满足的条件;③用坐标(x,y)表示条件,列出方程f(x,y)=0;④化简方程f(x,y)=0为最简形式;⑤证明所得方程即为所求的轨迹方程,注意验证.有时可以通过几何关系得到点的轨迹,根据定义法求得点的轨迹方程.
【例4】【福建省漳州市2018届高三上学期期末调研测试】直线过抛物线: 的焦点, 与交于, 两点,过点, 分别作的切线,交于点,则点的轨迹方程为( )
A. B. C. D.
【答案】A
易得抛物线在点处的切线方程为
同理可得抛物线在点处的切线方程为
联立,解得
再由①可得:
故
故点的轨迹方程为
故选
点睛:本题考查了直线与抛物线的综合,根据题目中的过点作切线,先设出点坐标,然后表示出切线方程,再由联立直线与抛物线方程解得结果,本题在求解过程中需要计算上的化简较为重要。
类型二、圆锥曲线的方程
【例5】【新疆乌鲁木齐市2018届高三第三次诊断性测验】的离心率为,为椭圆的一个焦点,若椭圆上存在一点与关于直线对称,则椭圆的方程为
A. B.
C. 或 D. 或
【答案】C
【例6】【山西省大同市与阳泉市2018届高三第二次教学质量监测】椭圆的左焦点为,过点作倾斜角为的直线与圆相交的弦长为,则椭圆的标准方程为( )
A. B. C. D.
【答案】B
【解析】分析:由左焦点为,可得,即,求得直线的方程,利用圆心到直线的距离、弦长公式,列方程求解,进而得到所求椭圆方程.
详解:由左焦点为,可得,即,
过点作倾斜角为的直线的方程为,
圆心到直线的距离,
由直线与圆相交的弦长为,
可得,解得,
则椭圆方程为,故选B.
点睛:本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系和数量积公式,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在轴上,还是在轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程或 ;③找关系:根据已知条件,建立关于、、的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
【例7】【河南省豫北豫南名校2018届高三上学期精英联赛】双曲线过点,渐进线方程为,则双曲线的标准方程是
A. B. C. D.
【答案】C
点睛:1.已知双曲线方程求渐近线:
2.已知渐近线 设双曲线标准方程
3,双曲线焦点到渐近线距离为,垂足为对应准线与渐近线的交点.
【例8】【福建省厦门市2018届高三下学期第一次质量检查】双曲线的渐近线方程为,焦距为,则该双曲线的标准方程是( )
A. B. C. 或 D. 或
【答案】C
点睛:(1)已知双曲线方程求渐近线: ;
(2)已知渐近线,设双曲线标准方程.
方法、规律归纳:
1.直接法求动点的轨迹方程的一般步骤
(1)建系——建立适当的坐标系;
(2)设点——设轨迹上的任一点P(x,y);
(3)列式——列出动点P所满足的关系式;
(4)代换——依条件式的特点,选用距离公式、斜率公式等将其转化为关于x,y的方程式,并化简;
(5)证明——证明所求方程即为符合条件的动点轨迹方程.
2.代入(相关点、转移)法求曲线方程时一般有两个动点,一个是主动的,另一个是次动的.
当题目中的条件同时具有以下特征时,一般可以用转移法求其轨迹方程:
② 个动点P(x,y)在已知方程的曲线上移动;
②另一个动点随P(x,y)的变化而变化;
③ 变化过程中P(x,y)和满足一定的规律.
3. 参数法:求动点轨迹时,有时会出现要求两动曲线交点的轨迹问题,这类问题常常通过解方程组得出交点(含参数)的坐标,再消去参数求出所求轨迹方程,该法经常与参数法并用。要注意以下问题:参数的选取要具有代表性,参数方程是动点的轨迹方程,在化简参数方程为普通方程的时候不能改变方程的解集.
4.求圆锥曲线的标准方程,主要利用定义法及待定系数法
实战演练:
1.【山东省济南市2018届高三第一次模拟考试】椭圆: ,若长轴长为6,且两焦点恰好将长轴三等分,则此椭圆的标准方程为( )
A. B.
C. D.
【答案】B
【解析】椭圆长轴为,焦点恰好三等分长轴,所以 椭圆方程为,故选B.
2.【山西省大同市与阳泉市2018届高三第二次教学质量监测】椭圆的左焦点为,过点作倾斜角为的直线与圆相交的弦长为,则椭圆的标准方程为( )
A. B. C. D.
【答案】B
【解析】分析:由左焦点为,可得,即,求得直线的方程,利用圆心到直线的距离、弦长公式,列方程求解,进而得到所求椭圆方程.
点睛:本题主要考查待定系数求椭圆方程以及直线与椭圆的位置关系和数量积公式,属于难题.用待定系数法求椭圆方程的一般步骤;①作判断:根据条件判断椭圆的焦点在轴上,还是在轴上,还是两个坐标轴都有可能;②设方程:根据上述判断设方程或 ;③找关系:根据已知条件,建立关于、、的方程组;④得方程:解方程组,将解代入所设方程,即为所求.
3.【百校联盟2018届TOP20一月联考(全国Ⅰ卷)】天文物理学和数学原理,月球绕地球运行时的轨道是一个椭圆.地球位于椭圆的两个焦点位置中的一个,椭圆上的点距离地球最近的点称为近地点.已知月球的近地点约为36万千米,月球轨道上点与椭圆两焦点构成的三角形面积约为 (万千米)2, ,则月球绕地球运行轨道的一个标准方程为( )
A. B. C. D.
【答案】B
4.【安徽省江淮六校2019届高三上学期开学联考】双曲线的虚轴长是实轴长的2倍,则双曲线的标准方程为( )
A. B.
C. D.
【答案】D
【解析】
【分析】
由题意得到关于m的方程,解方程求得m的值即可确定双曲线方程.
【点睛】
本题主要考查双曲线方程的求解,意在考查学生的转化能力和计算求解能力.
5.【安徽省亳州市2017-2018学年度第一学期期末高三质量检测】的两个焦点为,椭圆上两动点总使为平行四边形,若平行四边形的周长和最大面积分别为8和,则椭圆的标准方程可能为( )
A. B.
C. D.
【答案】C
【解析】由周长为8,可知,
由最大面积为,可知,
所以椭圆方程可以是,故选C。
点睛:本题考查椭圆的性质应用。本题中的平行四边形的基本型是焦点三角形,考查焦点三角形相关特征的应用,得, ,利用即可解得标准方程。
6.已知P为椭圆C上一点,F1,F2为椭圆的焦点,且,若|PF1|与|PF2|的等差中项为|F1F2|,则椭圆C的标准方程为( )
A. B. 或
C. D. 或
【答案】B
【解析】
【分析】
由题意,求得,根据椭圆的定义求得,进而得到,即可得到椭圆的方程.
【点睛】
本题主要考查了椭圆的定义及其标准方程的求解,其中解答中熟记椭圆的定义和椭圆的标准方程的形式是解答本题的关键,着重考查了推理与运算能力,属于基础题.
7.已知双曲线的一个焦点坐标为,且经点,则双曲线的标准方程为( )
A. B.
C. D.
【答案】A
【解析】
【分析】
双曲线的方程为(a>0,b>0),利用双曲线的一个焦点坐标为(,0),且经过点(﹣5,2),建立方程组,即可求出双曲线的标准方程.
【详解】
由题可设双曲线方程为,
把代入可得①,又,②,
由①②解得双曲线方程为.
故选A.
【点睛】
本题考查双曲线的简单性质,考查双曲线的方程,正确运用待定系数法是关键.
8.【福建省漳州市2018届高三1月调研测试】直线l过抛物线C:y2=4x的焦点,l与C交于A,B两点,过点A,B分别作C的切线,且交于点P,则点P的轨迹方程为 .
【答案】
9.【湖北省华中师范大学第一附属中学2018届高三5月押题考】双曲线的标准方程为
,且其焦点到渐近线的距离等于,则双曲线的标准方程为 .
【答案】.
【解析】分析:根据双曲线的标准方程求得双曲线的渐近线的方程,再根据焦点到渐近线的距离等于,利用点到直线距离公式,即可得出,即可求出,然后结合,从而求得双曲线的标准方程.
详解:∵双曲线的标准方程为
∴双曲线的渐近线的方程为,即.
∵其焦点到渐近线的距离等于
∴,即.
∵
∴
∴
∴双曲线的标准方程为
故答案为.
点睛:本题主要考查了双曲线的方程、渐近线方程,以及点到直线的距离公式的应用等方面的知识与运算技能,是常考题.确定,,的值是解答本题的关键.
10.【湖北省黄石市2018年高三五月适应性考试】M过点(3,2)且与直线y=1相切,则动圆圆心M的轨迹方程为 .
【答案】x2﹣6x﹣2y+12=0
【解析】
【分析】
设出圆心的坐标,利用已知条件列出方程即可求解
【点睛】
本题主要考查了轨迹方程,解题的关键是根据圆与直线相切,得到动圆到直线与到点的距离相等,属于基础题。
11.【浙江省嘉兴市2018届高三4月模拟测试】直角坐标系中,,动点满足,则点的轨迹方程是 ;轨迹为 .
【答案】 一个圆
【解析】设点,由题意:得:,整理得到点P的轨迹方程为,即,其轨迹为圆.
点睛:本题考查曲线轨迹方程的求法,考查计算能力,直接列方程是关键;常见的方法有:1、直接法;2、定义法;3、相关点法;4、待定系数法;5、参数法;6、交轨法,该题中利用的是直接法.
12.【四川省南充高级中学2018届高三考前模拟考试】作直线交轴于点,过点作交轴于点,延长至点,使得,则点的轨迹方程为 .
【答案】
【解析】分析:由题意可得点M为线段PN的中点,且FM是线段PN的垂直平分线,设点,点,由,可得点,设点,再由线段的中点坐标公式可得P的轨迹方程.
点睛:本题主要考查求点的轨迹方程的求法,把参数方程化为直角坐标方程.
13.【福建省漳州市2018届高三上学期期末调研测试】直线过抛物线: 的焦点, 与交于, 两点,过点, 分别作的切线,且交于点,则点的轨迹方程为 .
【答案】
【解析】不妨将抛物线翻转为,设翻转后的直线的方程为,翻转后的A,B两点的坐标分别为, ,则联立,得①,易得抛物线在点A处的切线方程为,同理可得抛物线在点B处的切线方程为
,联立得,再由①可得,所以,故原抛物线C相应的点P的轨迹方程为,故答案为.
14.【西藏拉萨市2018届高三第一次模拟考试】双曲线经过点,其一条渐近线方程为,则该双曲线的标准方程为 .
【答案】
15.【安徽省亳州市2017-2018学年度第一学期期末高三质量检测】曲线共焦点,且经过点的椭圆的标准方程为 .
【答案】
【解析】,且,所以,所以椭圆方程为。








