2019届二轮复习第2讲　平面向量与复数学案（全国通用）

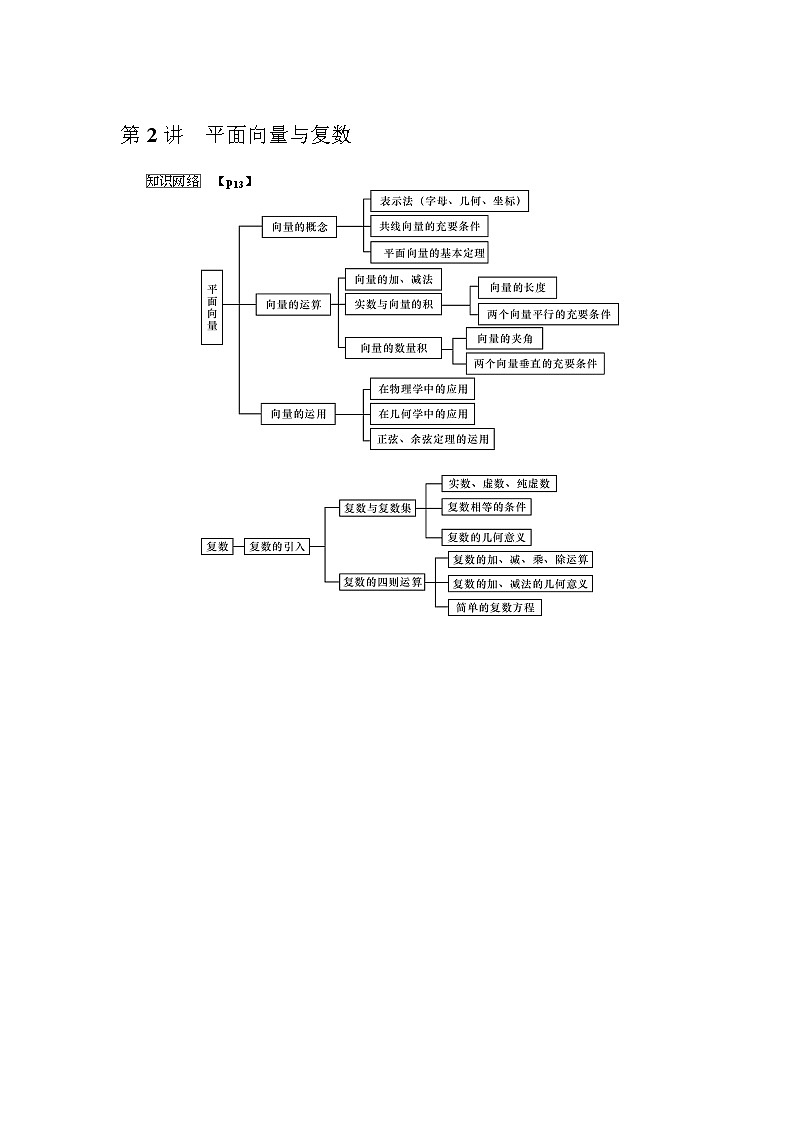
第2讲　平面向量与复数
　【p13】

　【p14】
年份
卷别
题号
考查内容
命题规律





2018




Ⅰ




1
复数代数形式的四则运算、复数的模



6
平面向量的线性运算



8
平面向量的数量积、
直线与抛物线的位置关系



Ⅱ




1
复数代数形式的四则运算



4
平面向量的数量积



Ⅲ




2
复数代数形式的四则运算



13
向量的线性运算、平行的判定与坐标表示



2017




Ⅰ




3
命题、复数的运算



13
向量的模、向量的数量积



Ⅱ




1
复数的运算



12
平面向量的数量积



Ⅲ




2
复数的运算、复数的模



12
平面向量基本定理、直线与圆的位置关系



2016




Ⅰ




2
复数相等的充要条件、复数的模



13
向量数量积的坐标运算



Ⅱ




1
复数的几何意义



3
向量的坐标运算和垂直关系



Ⅲ




2
共轭复数的概念、复数的运算



3
平面向量的数量积及坐标运算
　　复数的代数运算，还包括根据含z或某参数的等式求z(模|z|、实部a，虚部b)或参数，或根据两个复数的位置关系求某个复数．
向量的考法主要有：一、根据向量的坐标或几何表示，结合向量及其运算的几何意义，作平面向量的运算．二、在已知条件中将平面图形中的几何关系用向量运算表示，要求转化为代数关系或位置关系.


备 考 建 议　【p14】
对于平面向量要把握破解平面向量与“三角”交汇题的关键：一是巧“化简”，即活用诱导公式、同角三角函数的基本关系式、倍角公式、辅助角公式等对三角函数进行化简；二是会“转化”，把向量共线、向量垂直形式出现的条件还其本来面目，转化为“对应坐标乘积之间的关系”．
对于复数要掌握复数的概念、纯虚数、复数相等、复数的模、共轭复数等，以及复数的几何意义及四则运算(重点考查复数的乘除)．
典 例 剖 析　【p14】
探究一　复数的概念及运算
　　　　　　　　　　　　　　　　　　

例1(1) 已知i是虚数单位，若复数z＝－i的实部与虚部相等，则z的共轭复数＝(　　)
A．－1＋i
B．1＋i
C．1－i
D．－1－i
【解析】选C.
复数z＝－i＝1－ai.实部与虚部相等，则a＝－1.
z＝1＋i，＝1－i.故选C.
(2)已知复数z1＝－1＋2i，z2＝1－i，z3＝3－4i，它们在复平面上所对应的点分别为A、B、C，若＝λ＋μ(O为坐标原点，λ，μ∈R)，则λ＋μ的值是(　　)
A．1 B．2
C．3 D．4
【解析】选A.
因为复数z1＝－1＋2i，z2＝1－i，z3＝3－4i，它们所对应的点分别为A，B，C，∴A，B，C，因为点的坐标与以原点为起点的向量的坐标相同，所以由＝λ＋μ，得＝λ＋μ＝，∴解得∴λ＋μ＝1，故选A.
探究二　平面向量的线性运算
例2 (1)如图，AB是圆O的直径，C、D是圆O上的点，∠CBA＝60°，∠ABD＝30°，＝x＋y，则x＋y的值为(　　)

A．－ B．0
C．1 D．－
【解析】选B.
由题意得CD过圆心，所以＝2＝2(＋)＝2(－＋)⇒x＝2，y＝－2，x＋y＝0.
(2)在△ABC中，P为BC边中点，点A、B、C的对边长分别是a、b、c.若c＋a＋b＝0，则△ABC的形状为(　　)
A．等边三角形
B．等腰三角形非等边三角形
C．直角三角形
D．等腰直角三角形
【解析】选A.
将·都用基向量、表示出来可得c－(＋)－(－)＝0，
－＝0，
∴
∴a＝b＝c，∴△ABC为等边三角形．
【点评】用已知向量来表示一些未知向量是用向量解题的基本要求，除利用向量的加减法、实数与向量相乘外，还应充分利用平行四边形的一些定理．因此，在求向量时要尽可能转化到平行四边形或三角形中，选用从同一顶点出发的基本向量或首尾相连的向量，运用向量加、减法运算及实数与向量相乘来求解，即充分利用相等向量、相反向量和线段的比例关系，运用三角形的加法法则、平行四边形法则、三角形的减法法则，充分利用三角形的中位线、相似三角形对应边成比例的平面几何性质，把未知向量转化为与已知向量有直接关系的向量来求解．
探究三　平面向量的数量积
例3 (1)设四边形ABCD为平行四边形，||＝6，||＝4.若点M，N满足＝3，＝2，则·＝(　　)
A．20 B．15 C．9 D．6
【解析】选C.
解法一：如图，·＝·＝·
＝2－2＝×62－×42＝9.

解法二：特殊化处理，将平行四边形ABCD视为矩形，以A为坐标原点，以AB为x轴，AD为y轴建立平面直角坐标系，由已知可得M(6，3)，N(4，4)，∴＝(6，3)，＝(2，－1)，∴·＝6×2－3×1＝9.
【点评】涉及数量积和模的计算问题，通常有两种求解思路：①直接利用数量积的定义；②建立坐标系，通过坐标运算求解．
(2)已知单位向量e1与e2的夹角为α，且cos α＝，向量a＝3e1－2e2与b＝3e1－e2的夹角为β，则cos β＝__________．
【解析】
cos β＝＝
＝
＝＝＝.
【点评】在利用数量积的定义计算时，要善于将相关向量分解为图形中模和夹角已知的向量进行计算．
探究四　平面向量与三角函数结合问题
例4 已知向量a＝(cos α，sin α)，b＝(1＋cos β，－sin β)．
(1)若α＝，β∈(0，π)，且a⊥b，求β；
(2)若β＝α，求a·b的取值范围．
【解析】(1)∵a⊥b，
∴a·b＝cos α＋cos αcos β－sin αsin β＝0，
∵α＝，∴cos ＋cos cos β－sin sin β＝0，
整理得cos＝－，
∴β＋＝＋2kπ(k∈Z)或β＋＝＋2kπ(k∈Z)，
∵β∈(0，π)，∴β＝.
(2)a·b＝cos α＋cos2α－sin2α＝cos α＋2cos2α－1，
令t＝cos α，t∈[－1，1]，
∴a·b＝2t2＋t－1＝2－，
∴当t＝1时，(a·b)max＝2，
当t＝－时，(a·b)min＝－，
∴a·b的取值范围为.
【点评】在平面向量与三角函数的综合问题中，一方面用平面向量的语言表述三角函数中的问题，如利用向量平行、垂直的条件表述三角函数式之间的关系，利用向量模表述三角函数之间的关系等；另一方面可以利用三角函数的知识解决平面向量问题．在解决此类问题的过程中，只要根据题目的具体要求，在向量和三角函数之间建立起联系，就可以根据向量或者三角函数的知识解决问题．
探究五　平面向量与其他知识结合问题
例5 (1)如图，在直角梯形ABCD中，AB⊥AD，AB∥DC，AB＝2，AD＝DC＝1，图中圆弧所在圆的圆心为点C，半径为，且点P在图中阴影部分(包括边界)运动．若＝x＋y，其中x，y∈R，则4x－y的取值范围是(　　)

A. B.
C. D.
【解析】选B.
以A点为坐标原点，，方向为x轴，y轴正方向建立直角坐标系，设点P的坐标为P(m，n)，由意可知：＝x(2，0)＋y(－1，1)，
据此可得则
目标函数：z＝4x－y＝2m＋n，
其中z为直线系n＝－2m＋z的截距，
当直线与圆相切时，目标函数取得最大值3＋.
当直线过点时，目标函数取得最小值2，
则4x－y的取值范围是.
故选B.
【点评】本题同时考查平面向量基本定理和线性规划中的最值问题．求线性目标函数z＝ax＋by(ab≠0)的最值，当b>0时，直线过可行域且在y轴上截距最大时，z值最大，在y轴上截距最小时，z值最小；当b<0时，直线过可行域且在y轴上截距最大时，z值最小，在y轴上截距最小时，z值最大．应用平面向量基本定理表示向量的实质是利用平行四边形法则或三角形法则进行向量的加、减或数乘运算．用向量基本定理解决问题的一般思路是：先选择一组基底，并运用该基底将条件和结论表示成向量的形式，再通过向量的运算来解决．
(2)已知向量a，b满足|a|＝2|b|≠0，且关于x的函数f(x)＝－2x3＋3|a|x2＋6a·bx＋5在R上单调递减，则向量a，b夹角的取值范围是(　　)
A. B.
C. D.
【解析】选D.
设向量a，b的夹角为θ，
因为f(x)＝－2x3＋3|a|x2＋6a·bx＋5，
所以f′(x)＝－6x2＋6|a|x＋6a·b，
又函数f(x)在R上单调递减，
所以f′(x)≤0在R上恒成立，
所以Δ＝36|a|2－4×(－6)×(6a·b)≤0，
解得a·b≤－|a|2，因为a·b＝|a|·|b|cos θ，
且|a|＝2|b|≠0，
所以|a||b|cos θ＝|a|2cos θ≤－|a|2，
解得cos θ≤－，因为θ∈[0，π]，
所以向量a，b的夹角θ的取值范围是，故选D.
【点评】本题是平面向量和函数的交汇，由函数的性质把问题转化为平面向量问题，求解时应注意θ∈[0，π]．平面向量具有代数形式与几何形式的“双重型”，常与三角函数、解三角形、平面解析几何、函数、不等式等知识交汇命题，平面向量的“位置”为：一是作为解决问题的工具，二是通过运算作为命题条件．
规 律 总 结　【p15】
1．复数的基本概念与运算问题的解题思路：
(1)与复数的相关概念和复数的几何意义有关的问题，一般是先变形分离出实部和虚部，把复数的非代数形式化为代数形式，然后再根据条件，列方程(组)求解．
(2)与复数z的模|z|和共轭复数有关的问题，一般都要设出复数z 的代数形式z＝a＋bi(a，b∈R)，代入条件，用待定系数法解决．
2．当向量以几何图形的形式出现时，要把这个几何图形中的一个向量用其余的向量线性表示，就要根据向量加减法的法则进行，特别是减法法则很容易出错，向量＝－(其中O为任意一个点)，这个法则就是终点向量减去起点向量．
3．根据平行四边形法则，对于非零向量a，b，当|a＋b|＝|a－b|时，平行四边形的两条对角线长度相等，此时平行四边形是矩形，条件|a＋b|＝|a－b|等价于向量a，b互相垂直．
4．两个向量夹角的范围是[0，π]，在使用平面向量解决问题时要特别注意两个向量夹角可能是0或π的情况，如已知两个向量的夹角为钝角时，不单纯就是其数量积小于零，还要求不能反向共线．在解决有关向量夹角及共线问题时，要避免忽视向量共线时的方向性而导致错误．
5．数量积运算不适合结合律，即(a·b)·c≠a·(b·c)，这是由于(a·b)·c表示一个与c共线的向量，a·(b·c)表示一个与a共线的向量，而a与c不一定共线，因此(a·b)·c与a·(b·c)不一定相等．
6．若a＝0，则a·b＝0，但由a·b＝0，不能得到a＝0或b＝0，因为a⊥b时a·b＝0.
7．平面向量的综合运用主要体现在三角函数和平面解析几何中，在三角函数问题中平面向量的知识主要是给出三角函数之间的关系，解题的关键还是三角函数问题；解析几何中向量知识只是给出几何量的位置和数量关系，在解题中要善于根据向量知识分析解析几何中的几何关系．
高 考 回 眸　【p16】
　　　　　　　　　　　　　　　　　　

考题1[2018·全国卷Ⅰ]若z＝＋2i，则|z|＝(　　)
　　　　　　　　　　　　　　　　　　

A．0 B. C．1 D.
【解析】选C.
∵z＝＋2i＝＋2i＝＋2i＝i，∴|z|＝1，故选C.
【命题意图】本题考查了复数的四则运算和复数的模的概念，考查学生的计算能力．
考题2[2018·全国卷Ⅰ]在△ABC中，AD为BC边上的中线，E为AD的中点，则＝(　　)
A.－ B.－
C.＋ D.＋

【解析】选A.
作出示意图如图所示：
＝＋＝＋＝
－，故选A.
【命题意图】本题考查了平面向量的线性运算，考查了学生的逻辑思维能力．
考题3[2018·全国卷Ⅱ]已知向量a，b满足|a|＝1，a·b＝－1，则a·(2a－b)＝(　　)
A．4 B．3 C．2 D．0
【解析】选B.
a·(2a－b)＝2a2－a·b＝2－(－1)＝3，故选B.
【命题意图】本题考查了平面向量的数量积的概念，考查了学生的逻辑思维能力．
考题4[2018·全国卷Ⅲ]已知向量a＝(1，2)，b＝(2，－2)，c＝(1，λ)．若c∥(2a＋b)，则λ＝________________________________________________________________________.
【解析】
2a＋b＝(4，2)，因为c∥(2a＋b)，所以4λ＝2得λ＝.
【命题意图】本题考查了平面向量的坐标运算，考查了平面向量平行的条件．
考点限时训练　【p114】
A组　基础演练
1．已知复数z1＝k2－4＋(k2－5k＋6)i，z2＝3k＋(k2－5k＋6)i(k∈R)．若z1 A．2 B．3 C．2或3 D．不存在
【解析】选C.
由z1 解得k＝2或k＝3.故选C.
2．已知复数z＝|(－i)i|＋i5(i为虚数单位)，则复数z的共轭复数为(　　)
A．2－i B．2＋i
C．4－i D．4＋i
【解析】选A.
由题意知z＝|i＋1|＋i＝＋i＝2＋i，所以z＝2－i.故选A.
3．已知单位向量a，b满足a⊥(a＋2b)，则a与b夹角的余弦值为(　　)
A. B．－
C. D．－
【解析】选D.
由a⊥(a＋2b)，可得，a·(a＋2b)＝0，a2＋2a·b＝0，cos〈a·b〉＝＝－，所以选D.
4．向量a，b，c在正方形网格中，如图所示，若c＝λa＋μb(λ，μ∈R)，则＝(　　)

A．2 B．－2
C．6 D.
【解析】选A.
如图，以a，b的公共点为原点，建立直角坐标系，则a＝(－1，1)，因为a＝(－1，1)，b＝(5，2)，c＝(－3，－4)，因为c＝λa＋μb，所以有解得所以＝2，选A.
5．△ABC的外接圆的圆心为O，半径为1，若＋＝2，且||＝||，则向量在向量方向上的射影的数量为(　　)
A. B.
C．3 D．－
【解析】选A.
由于＋＝2，由向量加法的几何意义，O为边BC中点，因为△ABC的外接圆的圆心为O，半径为1，所以||＝||＝||＝||＝1，三角形应该是以BC边为斜边的直角三角形，斜边BC＝2AO＝2，直角边AB＝，所以∠ABC＝30°，

则向量在向量方向上的投影为|BA|cos 30°＝×＝，故选A.
6．已知AB⊥AC，AB＝AC，点M满足＝t＋(1－t)，若∠BAM＝，则t的值为(　　)
A.－
B.－1
C.
D.
【解析】选C.
由题意可得：＝t＋－t，
则－＝t－t，
即＝t⇒t＝.其中＝，由正弦定理：＝，
整理可得：t的值为.
B组　能力提升
7．现定义eiθ＝cos θ＋isin θ，其中i为虚数单位，e为自然对数的底数，θ∈R，且实数指数幂的运算性质对eiθ都适用，若a＝C50cos5θ－C52cos3θsin2θ＋C54cos θsin4θ，b＝C51cos4θsin θ－C53cos2θsin3θ＋C55sin5θ，那么复数a＋bi等于(　　)
A．cos 5θ＋isin 5θ
B．cos 5θ－isin 5θ
C．sin 5θ＋icos 5θ
D．sin 5θ－icos 5θ
【解析】选A.
a＋bi＝C50cos5θ－C52cos3θsin2θ＋C54cos θsin4θ＋
iC51cos4θsin θ－iC53cos2θsin3θ＋iC55sin5θ
＝C50cos5θ＋i2C52cos3θsin2θ＋i4C54cos θsin4θ
＋iC51cos4θsin θ＋i3C53cos2θsin3θ＋i5C55sin5θ
＝＝cos 5θ＋isin 5θ，选A.
*8.已知a，b是单位向量，a，b的夹角为90°，若向量c满足|c－a－b|＝2，则|c|的最大值为(　　)
A．2－
B.
C．2
D．2＋
【解析】选D.
依题意，设a，b分别是x轴与y轴正方向上的单位向量，
则a＝(1，0)，b＝(0，1)，a＋b＝(1，1)，设c＝(x，y)，
则c－a－b＝(x－1，y－1)，
因为|c－a－b|＝＝2，
所以(x－1)2＋(y－1)2＝4，
故c＝，点C的轨迹是以(1，1)为圆心，2为半径的圆，
圆心M(1，1)到原点的距离为，
则|c|的最大值为2＋.

9．如果复数z满足＝6，那么的最小值是__________．
【解析】1
复数z满足|z＋3i|＋|z－3i|＝6，
∴z的几何意义是以A(0，3)，B(0，－3)为端点的线段AB，
则|z＋1＋i|＝|z－(－1－i)|的几何意义为AB上的点到C(－1，－1)的距离，
则由图象知C到线段AB的距离的最小值为1.

*10.对任意两个非零的平面向量α和β，定义新的运算“⊗”：α⊗β＝.若两个非零的平面向量a，b满足a与b的夹角θ∈，且a⊗b和b⊗a都在集合中，则a⊗b＝__________．
【解析】
根据新定义，得
a⊗b＝＝＝cos θ，
b⊗a＝＝＝cos θ.
因为a⊗b和b⊗a都在集合中，设a⊗b＝，b⊗a＝(n1，n2∈Z)，那么(a⊗b)·(b⊗a)＝cos2θ＝.又θ∈，所以0