2019届二轮复习（理）线性规划学案（全国通用）

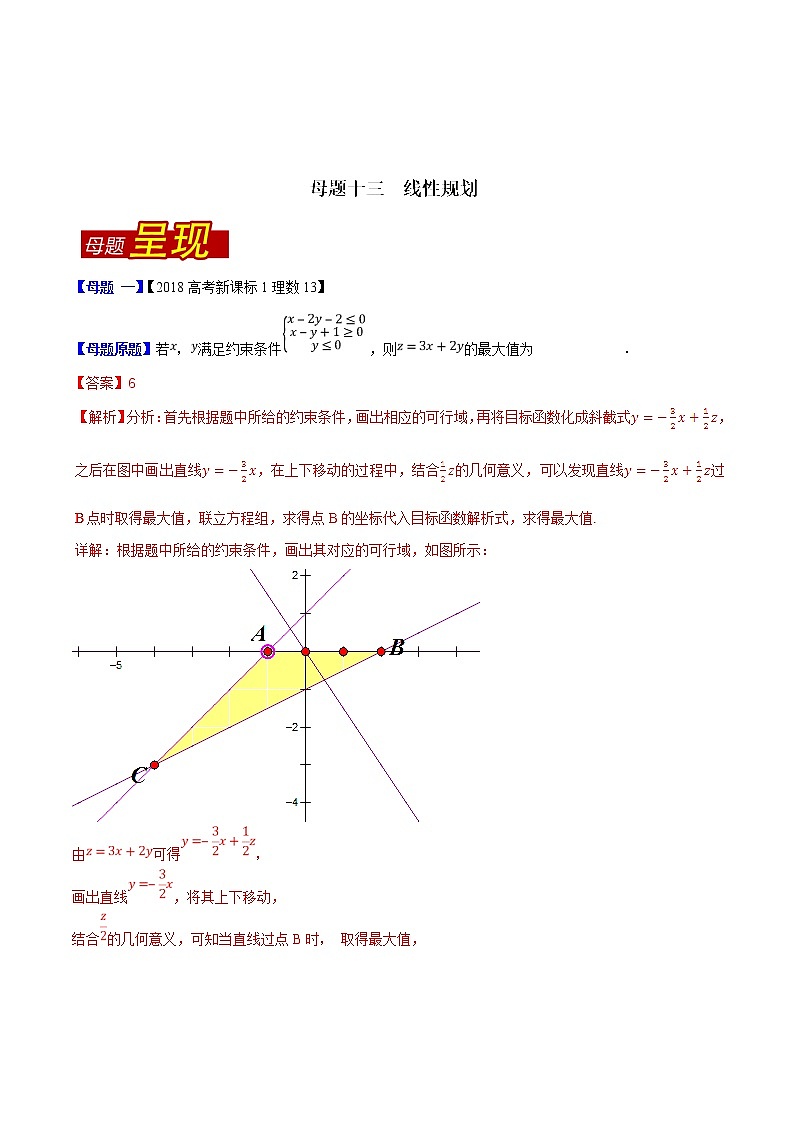
 【母题 一】【2018高考新课标1理数13】【母题原题】若，满足约束条件，则的最大值为             ．【答案】6由可得，画出直线，将其上下移动，结合的几何意义，可知当直线过点B时， 取得最大值，点睛：该题考查的是有关线性规划的问题，在求解的过程中，首先需要正确画出约束条件对应的可行域，之后根据目标函数的形式，判断 的几何意义，之后画出一条直线，上下平移，判断哪个点是最优解，从而联立方程组，求得最优解的坐标，代入求值，要明确目标函数的形式大体上有三种：斜率型、截距型、距离型；根据不同的形式，应用相应的方法求解.    【母题 二】【2017高考新课标1理数14】【母题原题】设x，y满足约束条件，则的最小值为                ．【答案】【解析】绘制不等式组表示的可行域，结合目标函数的几何意义可得目标函数在点处取得最小值 .【母题 三】【2016高考新课标1理数16】【母题原题】某高 技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg，乙材料1 kg，用5个工时；生产一件产品B需要甲材料0.5 kg，乙材料0.3 kg，用3个工时，生产一件产品A的利润为2100元，生产一件产品B的利润为900元.该企业现有甲材料150 kg，乙材料90 kg，则在不超过600个工时的条件下，生产产品A、产品B的利润之和的最大值为            元.【答案】]【解析】将变形，得，作直线：并平移，当直线经过点时， 取得最大值.    解方程组，得的坐标为.所以当，时，.故生产产品A、产品B的利润之和的最大值为元.【考点】线性规划的应用【名师点睛】线性规划也是高考中常考的知识点,一般以客观题的形式出现,基本题型是给出约束条件求目标函数的最值,常见的结合方式有：纵截距、斜率、两点间的距离、点到直线的距离,解决此类问题常利用数形结合.本题运算量较大,失分的一个主要原因是运算失误.【命题意图】1．会从实际情境中抽象出二元一次不等式组．　2.了解二元一次不等式的几何意义，能用平面区域表示二元一次不等式组．　3.会从实际情境中抽象出一些简单的二元线性规划问题，并能加以解决．【命题规律】1．二元一次不等式(组)的解集满足二元一次不等式(组)的x和y的取值构成有序数对(x，y)，所有这样的有序数对(x，y)构成的集合称为二元一次不等式(组)的解集．2．二元一次不等式所表示的平面区域一般地，二元一次不等式Ax＋By＋C>0在平面直角坐标系中表示直线Ax＋By＋C＝0某一侧所有点组成的平面区域．我们把直线画成虚线以表示区域不包括边界．当我们在坐标系中画不等式Ax＋By＋C≥0所表示的平面区域时，此区域应包括边界，则把边界画成实线．3．二元一次不等式表示平面区域的判断方法直线l：Ax＋By＋C＝0把坐标平面内不在直线l上的点分为两部分，直线l的同一侧点的坐标使式子Ax＋By＋C的值具有相同的符号，并且两侧点的坐标使Ax＋By＋C的值的符号相反，一侧都大于0，另一侧都小于0.4．线性规划中的基本概念约束条件：由变量x，y组成的不等式组.线性约束条件：由x，y的线性不等式(或方程)组成的不等式组；目标函数：关于x，y的函数，如 ＝2x＋3y等；线性目标函数：关于x，y的线性目标函数.可行解：满足线性约束条件的解.可行域：所有可行解组成的平面区域.最优解：使目标函数取得最大值或最小值的可行解线性规划问题：在线性约束条件下求线性目标函数的最大值或最小值问题【方法总结】1．求目标函数最值的一般步骤：一画二移三求．其关键是准确作出可行域，理解目标函数的意义．2．常见的目标函数有：(1)截距型：形如 ＝ax＋by.求这类目标函数的最值常将函数 ＝ax＋by转化为直线的斜截式：y＝－x＋，通过求直线的截距的最值间接求出 的最值．(2)距离型：形如 ＝(x－a)2＋(y－b)2.(3)斜率型：形如 ＝.3．解线性规划应用题的步骤(1)转化——设元，写出约束条件和目标函数，从而将实际问题转化为线性规划问题； 学  ](2)求解——解这个纯数学的线性规划问题(3)作答——将数学问题的答案还原为实际问题的答案．  1．【2018年北京市石景山区高三统一测试】设满足约束条件则下列不等式恒成立的是（    ）A.     B.     C.     D. 【答案】C2．【浙江省杭州市第二中学2018届高三仿真考】已知不等式组表示的平面区域的面积为9，若点， 则的最大值为（   ）A. 3    B. 6    C. 9    D. 12【答案】C点睛：该题考查的是有关线性规划的问题，在求解的过程中，首先需要正确画出约束条件对应的可行域，之后根据目标函数的形式，判断 的几何意义，之后画出一条直线，上下平移，判断哪个点是最优解，从而联立方程组，求得最优解的坐标，代入求值，要明确目标函数的形式大体上有三种：斜率型、截距型、距离型；根据不同的形式，应用相应的方法求解.     3．【安徽省安庆市第一中学2018届高三热身考】记不等式组的解集为，若，则实数的最小值是(    )A. 0    B. 1    C. 2    D. 4【答案】C点睛：本题在求解时，首先要根据约束条件正确画出可行域，之后根据目标函数的形式，判断参数的几何意义，判断哪个点是最优解，从而联立方程组，求得最优解的坐标，代入求值即可.4．【北京市十一学校2018届高三三模】已知实数满足若的最小值是-5，则实数取值集合是（  ）A.     B.     C.     D. 【答案】B【解析】分析：画出满足约束条件的可行域，求出目标函数的最大值，从而建立关于m的等式，即可得出答案.解析：由得，作出不等式组对应的平面区域如图：点睛：与二元一次不等式(组)区域有关问题的解决方法    (1)求解与平面区域有关的问题的关键是作出平面区域，在含有参数的问题中注意对参数的取值范围进行讨论；(2)在含有参数的二元一次不等式组所表示的平面区域问题中，首先把不含参数的平面区域确定好，然后用数形结合的方法根据参数的不同取值情况画图观察区域的形状，根据求解要求确定问题的答案．5．【福建省莆田第九中学2018届高三高考模拟】设关于,的不等式组,表示的平面区域内存在点，满足,求得取值范围是（  ）A.     B.     C.     D. 【答案】B要使可行域存在，必有，平面区域内存在点，满足,等价于可行域包含直线上的点，只要边界点在直线的上方，且在直线下方，故得不等式组 ，解之得，取值范围是，故选B.点睛：本题主要考查可行域、含参数约束条件，属于难题.含参变量的线性规划问题是近年来高考命题的热点，由于参数的引入，提高了思维的技巧、增加了解题的难度， 此类问题的存在增加了探索问题的动态性和开放性，此类问题一般从目标函数的结论入手，对目标函数变化过程进行详细分析，对变化过程中的相关量的准确定位，是求最优解的关键.    6．【湖北省华中师范大学第一附属中学2018届高三5月押题考】已知变量，满足，则的取值范围是（  ）A.     B.     C.     D. 【答案】B的几何意义为可行域内的动点与定点连线的斜率.∵，∴的取值范围是故选B.点睛：本题主要考查简单线性规划．解决此类问题的关键是正确画出不等式组表示的可行域，将目标函数赋予几何意义；求目标函数的最值的一般步骤为：一画二移三求．其关键是准确作出可行域，理解目标函数的意义．常见的目标函数有：（1）截距型：形如，求这类目标函数的最值常将函数 转化为直线的斜截式： ，通过求直线的截距的最值间接求出的最值；（2）距离型：形如 ；（3）斜率型：形如，而本题属于斜率型.7．【湖北省2018届高三5月冲刺】已知实数、满足条件，则的最大值为（    ）A.     B.     C.     D. 1  ]【答案】A点睛：线性规划问题，首先明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线，其次确定目标函数的几何意义，是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等，最后结合图形确定目标函数最值取法、值域范围.    8．【山东省潍坊市青州市2018届高三第三次高考模拟考试】某旅行社租用两种型号的客车安排名客人旅行，两种车辆的载客量分别为人和人，租金分别为元/辆和元/辆，旅行社要求租车总数不超过辆，且型车不多于型车辆，则租金最少为（   ）A. 元    B. 元    C. 元    D. 元【答案】C   ]9．【湖南省长沙市长郡中学2018届高考模拟卷（二）】已知变量，满足条件则目标函数的最大值为（   ）A.     B.     C.     D. 【答案】C其中为向量与的夹角，由图可知，时有最小值，在直线上时，有最大值，即，，目标函数的最大值为，故选C.点睛：本题主要考查线性规划中，利用可行域求目标函数的最值，属于简单题.求目标函数最值的一般步骤是“一画、二找、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移或旋转变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.10．【安徽省江南十校2018届高三冲刺联考（二模）】已知实数，满足，则的最大值是（   ）A.     B.     C.     D. 【答案】B点睛：线性规划问题中，关键是作出可行域，作出目标函数对应的直线，然后平移直线得出最优解，如果目标函数不是一次的，一般要确定其几何意义，如直线的斜率，两点间距离等，再利用几何意义求解．11．【福建省两大名校2018届高三下学期第一次模拟考试】若变量、满足约束条件，则的最大值为               .【答案】点睛：本小题主要考查线性规划知识、作图、识图能力及计算能力，以及利用几何意义求最值，是基础题.12．【江苏省南通市2018届高三最后一卷】已知实数满足，且恒成立，则实数的最小值是          ．【答案】.【解析】分析：若恒成立，满足的可行域在直线下面，结合图形可得结果.详解：点睛：本题主要考查可行域、含参数目标函数最优解，属于难题.含参变量的线性规划问题是近年来高考命题的热点，由于参数的引入，提高了思维的技巧、增加了解题的难度， 此类问题的存在增加了探索问题的动态性和开放性，此类问题一般从目标函数的结论入手，对目标函数变化过程进行详细分析，对变化过程中的相关量的准确定位，是求最优解的关键.    13．【福建省三明市第一中学2018届高三模拟卷（一）】已知实数，满足约束条件，且的最小值为3，则常数          ．【答案】-2.【解析】分析：画出可行域，将变形为，平移直线由图可知当直经过点时，直线在轴上的截距最小，根据的最小值为列方程求解即可.详解：画出表示的可行域，如图，点睛：本题主要考查线性规划中，利用可行域求目标函数的最值，属于简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.14．【江苏省南通市2018届高三最后一卷】甲、乙两种食物的维生素含量如下表： 维生素（单位/）维生素（单位/）甲乙分别取这两种食物若干并混合，且使混合物中维生素的含量分别不低于单位，则混合物重量的最小值为          ．【答案】.【解析】分析：设甲食物重，乙两食物重，则，混合物重，利用线性规划可得结果.详解：设甲食物重，乙两食物重，的含量分别不低于单位，，由，得，，混合物重，平移直线， 学+ + ]由图知，当直线过时，最小值为，故答案为.点睛：本题主要考查线性规划中利用可行域求目标函数的最值，属简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的定点就是最优解）；（3）将最优解坐标代入目标函数求出最值.