

2020届二轮复习(理)中难提分突破特训(三)作业 练习
展开中难提分突破特训(三)
1.如图,三棱柱ABC-A1B1C1中,BC=BB1,∠B1BC=60°,B1C1⊥AB1.
(1)证明:AB=AC;
(2)若AB⊥AC,且AB1=BB1,求二面角A1-CB1-C1的余弦值.
解 (1)证明:如图,取BC的中点O,连接AO,OB1.
因为BC=BB1,∠B1BC=60°,
所以△BCB1是等边三角形,
所以B1O⊥BC,
又BC∥B1C1,B1C1⊥AB1,
所以BC⊥AB1,
所以BC⊥平面AOB1,
所以BC⊥AO,由三线合一可知△ABC为等腰三角形,
所以AB=AC.
(2)设AB1=BB1=2,则BC=BB1=2.
因为AB⊥AC,所以AO=1.
又因为OB1=,
所以OB+AO2=AB,所以AO⊥OB1.
以O为坐标原点,向量的方向为x轴的正方向,建立如图所示的空间直角坐标系Oxyz,则O(0,0,0),C(-1,0,0),A1(-1,,1),B1(0,,0),=(0,,1),=(1,,0),
设平面A1B1C的一个法向量为n=(x,y,z),
则即可取n=(,-1,),
由(1)可知,平面CB1C1的法向量可取=(0,0,1),
所以cos〈,n〉==,
由图示可知,二面角A1-CB1-C1为锐二面角,
所以二面角A1-CB1-C1的余弦值为.
2.已知函数f(x)=2sinxsin.
(1)求函数f(x)的单调递增区间;
(2)锐角△ABC的角A,B,C所对的边分别是a,b,c,角A的平分线交BC于D,直线x=A是函数f(x)图象的一条对称轴,AD=BD=2,求边a.
解 (1)∵f(x)=2sinxsin,
∴f(x)=2sinxsinx·+2sinxcosx·
=+sin2x=sin2x-cos2x+
=sin+.
令-+2kπ≤2x-≤+2kπ,k∈Z,得
-+kπ≤x≤+kπ,k∈Z.
即函数f(x)的单调递增区间为,k∈Z.
(2)∵x=A是函数f(x)图象的一条对称轴,
∴2A-=+kπ,k∈Z.∴A=+,k∈Z.
又△ABC是锐角三角形,∴A=.
在△ABD中,∠BAD=,BD=,AD=2,
由正弦定理,得=,
∴sinB=.∴B=.
∴C=π--=.∠CDA=+=.
∴AC=AD=2.
在△ABC中,由正弦定理,得=,
∴BC=a=.
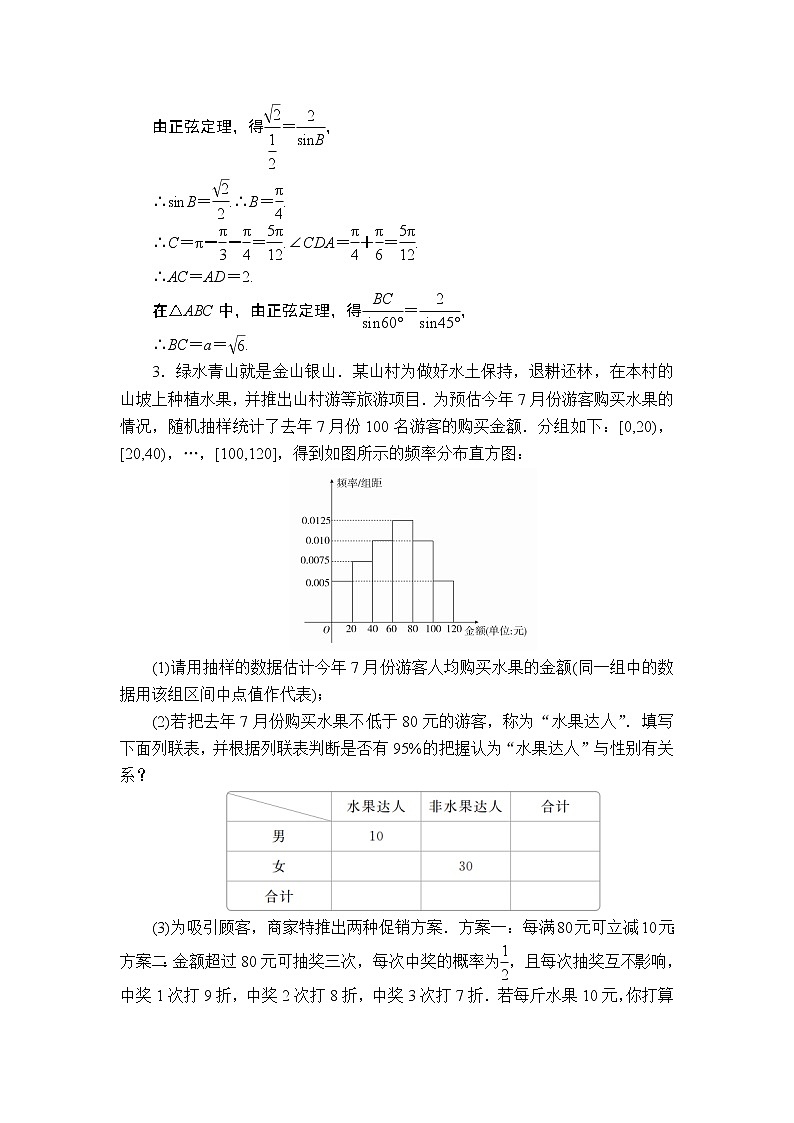
3.绿水青山就是金山银山.某山村为做好水土保持,退耕还林,在本村的山坡上种植水果,并推出山村游等旅游项目.为预估今年7月份游客购买水果的情况,随机抽样统计了去年7月份100名游客的购买金额.分组如下:[0,20),[20,40),…,[100,120],得到如图所示的频率分布直方图:
(1)请用抽样的数据估计今年7月份游客人均购买水果的金额(同一组中的数据用该组区间中点值作代表);
(2)若把去年7月份购买水果不低于80元的游客,称为“水果达人”.填写下面列联表,并根据列联表判断是否有95%的把握认为“水果达人”与性别有关系?
(3)为吸引顾客,商家特推出两种促销方案.方案一:每满80元可立减10元;方案二:金额超过80元可抽奖三次,每次中奖的概率为,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.若每斤水果10元,你打算购买12斤水果,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
参考公式和数据:K2=,n=a+b+c+d.
临界值表:
P(K2≥k0) | 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
k0 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
解 (1)=(10×0.005+30×0.0075+50×0.010+70×0.0125+90×0.010+110×0.005)×20=62.
估计今年7月份游客人均购买水果的金额为62元.
(2)列联表如下:
K2=≈4.762>3.841,
因此有95%的把握认为“水果达人”与性别有关系.
(3)若选方案一:则需付款10×12-10=110元;
若选方案二:设付款X元,则X的可能取值为84,96,108,120.
P(X=84)=C3=,
P(X=96)=C2×=,
P(X=108)=C××2=,
P(X=120)=C3=,
所以E(X)=84×+96×+108×+120×=102.
因为102<110,所以选择方案二更划算.
4.在平面直角坐标系xOy中,曲线C的参数方程为(θ为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系.
(1)求C的极坐标方程;
(2)若直线l1,l2的极坐标方程分别为θ=(ρ∈R),θ=(ρ∈R),设直线l1,l2与曲线C的交点为O,M,N,求△OMN的面积.
解 (1)由参数方程(θ为参数),
得普通方程为x2+(y-2)2=4,
所以C的极坐标方程为ρ2cos2θ+ρ2sin2θ-4ρsinθ=0,即ρ=4sinθ.
(2)不妨设直线l1:θ=(ρ∈R)与曲线C的交点为O,M,则ρM=|OM|=4sin=2,
又直线l2:θ=(ρ∈R)与曲线C的交点为O,N,
则ρN=|ON|=4sin=2.
又∠MON=,
所以S△OMN=|OM|·|ON|=×2×2=2.
5.已知函数f(x)=|3x+2|.
(1)解不等式:f(x)<4-|x-1|;
(2)已知m>0,n>0,m+n=1,若对任意的x∈R,m>0,n>0,不等式|x-a|-f(x)≤+(a>0)恒成立,求正数a的取值范围.
解 (1)由题意得不等式为|3x+2|+|x-1|<4.
①当x≥1时,原不等式化为4x+1<4,解得x<,不符合题意;
②当-<x<1时,原不等式化为2x+3<4,解得x<,∴-<x<;
③当x≤-时,原不等式化为-4x-1<4,解得x>-,∴-<x≤-.
综上可得-<x<,
∴原不等式的解集为.
(2)∵m>0,n>0,m+n=1,
∴+=(m+n)
=2++≥2+2=4.
当且仅当=且m+n=1,m>0,n>0,
即m=n=时等号成立,∴min=4.
由题意得|x-a|-|3x+2|≤4(a>0)恒成立,
①当x≥a时,可得x-a-3x-2≤4恒成立,即-a≤2x+6恒成立,∴-a≤(2x+6)min=2a+6,
由a>0,可得上式显然成立;
②当-<x<a时,可得a-x-3x-2≤4恒成立,即a≤4x+6恒成立,∵4x+6>,∴a≤;
③当x≤-时,可得a-x+3x+2≤4恒成立,即a≤2-2x恒成立,∴a≤(2-2x)min=.
综上可得0<a≤,
∴正数a的取值范围是.








