

2020届二轮复习算法案例教案(全国通用)
展开
1.更相减损术——求两个整数的最大公约数的算法
如何找到一种算法,对任意两个正整数都能快速地求出它们的最大公约数呢?
更相减损术的步骤:
以两个数中较大的数减去较小的数,以差数和较小的数构成一对新的数,对这一对数再用大数减小数,以同样的操作一直做下去,直到产生一对相等的数,此数就是这两个数的最大公约数.
等值算法:用“更相减损术”设计出来的算法求最大公约数的算法称为“等值算法”,用等值算法可以求任意两个正整数的最大公约数.
<教师备案>
《九章算法》是中国古代的数学专著,其中的“更相减损术”可以用来求两个数的最大公约数.以具体的例子来说明更相减损术求最大公约数的原理:
以求和的最大公约数为例:
,
每次操作后得到的两个数与前两个数的最大公约数相同,而且逐渐减少,故总能得到相等的两个数,即为所求的最大公约数.
2.辗转相除法
又称欧几里得算法,是由欧几里得在公元前300年左右首先提出来的求两个数的最大公约数的算法。
辗转相除法的步骤:
对于给定的两个数,以其中较大的数除以较小的数得到一个余数,将较小的数与余数看成一对新的数,重复上面的步骤,直到余数为零为止,此时上一步中较小的数即为所求的最大公约数。
以求和的最大公约数为例:
,故即为所求。
3.秦九韶算法——求多项式的值的算法
对于任意一个元的多项式,如何更快地计算它在某点所取到的值?
秦九韶算法:
已知一个多项式函数,计算多项式在某点处的函数值的一种算法,是我国古代数学家秦九韶提出的,
具体如下.
对任意一个元多项式,
改写成如下形式:
,
求多项式的值时,先计算最内层括号内的一次多项式的值,即,
然后由内向外逐层计算一次多项式的值,即,,,.
这样,求一个次多项式的值,就转化为求个一次多项式的值.
令,则递推公式为,其中.
到目前为止,此算法仍然是世界上多项式求值的最先进的算法.
秦九韶算法与其它算法在计算量上面的比较:,
⑴直接求和法:先计算各个单项式的值,再把它们相加,
乘法次数为,加法次数;
⑵逐项求和法:先计算的各项幂的值,再分别相乘,计算幂值需要乘法次,将幂值与多项式系数相乘需要乘法次,故共需要乘法次,加法次.
此方法对直接求和法有所改进,但仍然比秦九韶算法计算量大很多.
⑶秦九韶算法:计算量仅为乘法次,加法次.
题型一:辗转相除法与更相减损术
【例1】 我国古代数学发展一直处于世界领先水平,特别是宋、元时期的“算法”,其中可以同欧几里德辗转相除法相媲美的是 .
【考点】辗转相除法与更相减损术 【难度】1星 【题型】填空
【关键词】无
【解析】
【答案】更相减损术.
【例2】 用更相减损术求与的最大公约数.
【考点】辗转相除法与更相减损术 【难度】1星 【题型】解答
【关键词】无
【解析】 ,故与的最大公约数为.
【答案】
【例3】 用辗转相除法计算和的最大公约数时,需要做的除法次数是 ( )
A.1 B.2 C.3 D.4
【考点】辗转相除法与更相减损术 【难度】1星 【题型】选择
【关键词】无
【解析】 ,,故只需要两步计算.
【答案】B
【例4】 分别用自然语言、程序框图描述等值算法,并写出等值算法的程序.
【考点】辗转相除法与更相减损术 【难度】2星 【题型】解答
【关键词】无
【解析】 自然语言:
S1:输入两个正整数;
S2:如果不等于,则执行第三步(S3);否则转到第五步(S5);
S3:把的差赋予;
S4:如果,则把赋予,把赋予;否则把赋予,执行第二步(S2);
S5:输出最大公约数.
程序(A版Basic语言):
INPUT (“a,b=”);a,b
WHILE a<>b
IF a>b THEN a=a-b
ELSE b=b-a
END IF
WEND
PRINT b
END
程序(B版Scilab程序语言):
a=input(“a=”);
b=input(“b=”);
while a<>b
if a>b
a=a-b;
else
b=b-a;
end
end
print(%io(2),b)
程序框图如下:
【答案】
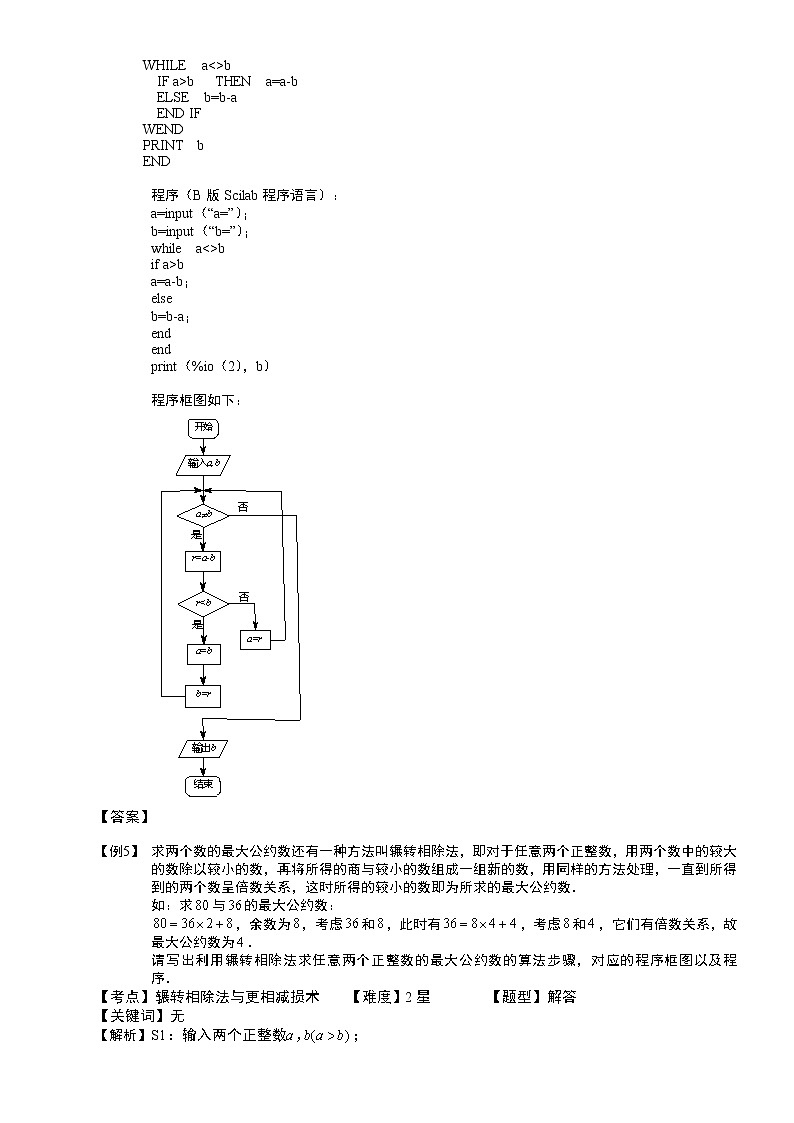
【例5】 求两个数的最大公约数还有一种方法叫辗转相除法,即对于任意两个正整数,用两个数中的较大的数除以较小的数,再将所得的商与较小的数组成一组新的数,用同样的方法处理,一直到所得到的两个数呈倍数关系,这时所得的较小的数即为所求的最大公约数.
如:求与的最大公约数:
,余数为,考虑和,此时有,考虑和,它们有倍数关系,故最大公约数为.
请写出利用辗转相除法求任意两个正整数的最大公约数的算法步骤,对应的程序框图以及程序.
【考点】辗转相除法与更相减损术 【难度】2星 【题型】解答
【关键词】无
【解析】 S1:输入两个正整数;
S2:计算除以所得的余数;
S3:如果,则执行S4,否则转到S6;
S4:把赋予,把赋予;
S5:执行S2;
S6:输出.
辗转相除法(B版)程序:
a=input(“a=”);
b=input(“b=”);
r=1;
while r<>0
r=mod(a,b);
a=b;
b=r;
end
print(%io(2),b)
//r=mod(a,b)的含义是r为a除以b的余数.
辗转相除法(A版)程序:
INPUT (“a,b=”);a,b
DO
r=a MOD b
a=b
b=r
LOOP UNTIL r=0
PRINT b
END
// r=a MOD b的含义是r为a除以b的余数
【答案】
【例6】 分别用辗转相除法与更相减损术求与的最大公约数,并且由此比较这两种算法.
【考点】辗转相除法与更相减损术 【难度】2星 【题型】解答
【关键词】无
【解析】 更相减损术:
故它们的最大公约数为.
辗转相除法:
;;故它们的最大公约数为.
联系:都是求最大公约数的方法;
区别:①计算上辗转相除法以除法为主,更相减损术以减法为主;
②计算次数上,辗转相除法计算次数相对较少,特别是当两个数差别较大时区别明显;
③从结果输出的时候看,辗转相除法当“余数为”时输出“除数”,更相减损术当“差和减数相等”时输出“差”.
【答案】
【例7】 分别用更相减损术与辗转相除法求和的最大公约数,并写出用等值算法计算的程序与程序框图.
【考点】辗转相除法与更相减损术 【难度】2星 【题型】解答
【关键词】无
【解析】 更相减损术:
,
故它们的最大公约数为;
辗转相除法:
;;;
故它们的最大公约数为;
等值算法的程序(B版):
a=153;b=119;
while a<>b
if a>b
a=a-b;
else
b=b-a;
end
end
print(%io(2),b)
等值算法的程序(A版):
a=153
b=119
while a<>b
if a>b then a=a-b
else
end if
wend
print b
程序框图
【答案】
题型二:秦九韶算法
【例8】 用秦九韶算法求次多项式,当时,求需要算乘方、乘法、加法的次数分别为( )
A. B. C. D.
【考点】秦九韶算法 【难度】2星 【题型】选择
【关键词】无
【解析】
【答案】D
【例9】 用秦九韶算法计算多项式在时的值.
【考点】秦九韶算法 【难度】2星 【题型】解答
【关键词】无
【解析】 ;
,;
,;
,;
,;
,;
,.
∴.
【答案】
【例10】 已知次多项式.如果在一次算法中,计算的值需要次乘法,计算的值共需次运算(次乘法,次加法),那么计算的值共需要______次运算.
【考点】秦九韶算法 【难度】2星 【题型】填空
【关键词】2018,北京,高考
【解析】 次运算.
【答案】
【例11】 设计利用秦九韶算法计算次多项式当时的值的程序框图.
【考点】秦九韶算法 【难度】2星 【题型】解答
【关键词】无
【解析】 程序框图如下:
【答案】
【例12】 写出用秦九韶算法计算任一个元多项式在某点的值的程序,以及对应的程序框图.
【考点】秦九韶算法 【难度】2星 【题型】解答
【关键词】无
【解析】 程序(B版):
x=input(“x=”);
n=input(“n=”);
a(0)=input(“a(0)=”);
a(1)=input(“a(1)=”);
…
a(n)=input(“a(n)=”);
i=1;
v=a(n);
while i<=n
v=v*x+a(n-i);
i=i+1;
end
print(%io(2),v)
程序框图:
【答案】








