人教版九年级上册24.2.2 直线和圆的位置关系获奖课件ppt

这是一份人教版九年级上册24.2.2 直线和圆的位置关系获奖课件ppt，共60页。PPT课件主要包含了直线和圆的位置关系，填一填，练一练判断正误，要点归纳，连接中考，基础巩固题，能力提升题，拓广探索题，切线的判定及性质，对比思考等内容，欢迎下载使用。

如图，在太阳升起的过程中，太阳和地平线会有几种位置关系？我们把太阳看作一个圆，地平线看作一条直线，由此你能得出直线和圆的位置关系吗？
2. 会从公共点的个数或d和r的数量关系判定直线和圆的位置关系.
1. 知道直线和圆的位置关系及有关概念.
问题1 如果我们把太阳看成一个圆，地平线看成一条直线，那你能根据直线和圆的公共点个数想象一下，直线和圆有几种位置关系吗？
用公共点个数判断直线与圆的位置关系
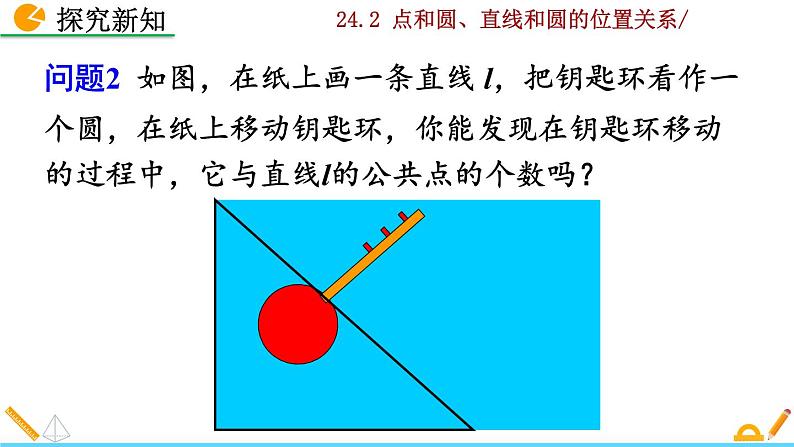
问题2 如图，在纸上画一条直线 l，把钥匙环看作一个圆，在纸上移动钥匙环，你能发现在钥匙环移动的过程中，它与直线l的公共点的个数吗？
问题3 请同学在纸上画一条直线l，把硬币的边缘看作圆，在纸上移动硬币，你能发现直线和圆的公共点个数的变化情况吗？公共点个数最少时有几个？最多时有几个？
直线和圆有唯一的公共点（即直线和圆相切）时，这条直线叫做圆的切线（如图直线l），这个唯一的公共点叫做切点（如图点A）.
（1）直线与圆最多有两个公共点.（2）若直线与圆相交，则直线上的点都在圆上. （3）若A是⊙O上一点，则直线AB与⊙O相切. （4）若C为⊙O外一点，则过点C的直线与⊙O相交或相离. （5）直线a 和⊙O有公共点，则直线a与⊙O相交.
问题1 同学们用直尺在圆上移动的过程中，除了发现公共点的个数发生了变化外，还发现有什么量也在改变？它与圆的半径有什么样的数量关系呢？
用数量关系判断直线与圆的位置关系
知识链接： 点到直线的距离是指从直线外一点（A）到直线（l）的垂线段（OA）的长度.
问题2 怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢？
直线和⊙O相交
直线和⊙O相离
根据直线和圆相交、相切、相离的定义：
活动根据直线和圆相切的定义，经过点A用直尺近似地画出⊙O的切线.
例1 在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，r为半径的圆与AB有怎样的位置关系？为什么？(1) r=2cm；(2) r=2.4cm； (3) r=3cm．
分析：要了解AB与⊙C的位置关系，只要知道圆心C到AB的距离d与r的关系．已知r，只需求出C到AB的距离d.
利用r和d的大小关系识别直线与圆的位置关系
解：过C作CD⊥AB，垂足为D.
根据三角形的面积公式有
即圆心C到AB的距离d=2.4cm.
所以 (1)当r=2cm时,
记住：斜边上的高等于两直角边的乘积除以斜边.
（2）当r=2.4cm时,有d=r.
（3）当r=3cm时，有d因此，⊙C和AB相交.
1. Rt△ABC,∠C=90°AC=3cm，BC=4cm，以C为圆心画圆，当半径r为何值时，圆C与直线AB没有公共点？
当0cm＜r＜2.4cm或r＞4cm时,⊙C与线段AB没有公共点.
2. Rt△ABC,∠C=90，AC=3cm，BC=4cm，以C为圆心画圆，当半径r为何值时，圆C与线段AB有一个公共点？当半径r为何值时，圆C与线段AB有两个公共点？
当r=2.4cm或3cm ＜r≤4cm时,⊙C与线段AB有一个公共点.
当2.4cm＜r≤3cm 时,⊙C与线段AB有两公共点.
3. 圆的直径是13cm，如果直线与圆心的距离分别是 （1）4.5cm ；（2） 6.5cm ；（3） 8cm； 那么直线与圆分别是什么位置关系？ 有几个公共点？
例2 如图，Rt△ABC的斜边AB=10cm,∠A=30°.
以点C为圆心，当半径为多少时，AB与☉C相切？
解：过点C作边AB上的高CD.
∵∠A=30°，AB=10cm,
4. 如图，已知∠AOB=300，M为OB上一点，且 OM=5cm，以M为圆心、r为半径的圆与直线OA 有怎样的位置关系？为什么？
(3) r=2.5cm
1.已知⊙O的半径为5cm，圆心O到直线l的距离为5cm，则直线l与⊙O的位置关系为（　　）A．相交 B．相切C．相离 D．无法确定
2.已知直线y=kx（k≠0）经过点（12，﹣5），将直线向上平移m（m＞0）个单位，若平移后得到的直线与半径为6的⊙O相交（点O为坐标原点），则m的取值范围为 ．
1.看图判断直线l与☉O的位置关系？
2．直线和圆相交，圆的半径为r, 且圆心到直线的距离为5，则有（ ） A. r < 5 B. r > 5 C. r = 5 D. r ≥ 5
3. ☉O的最大弦长为8，若圆心O到直线l的距离为d=5，则直线l与☉O .
4. ☉O的半径为5,直线l上的一点到圆心O的距离是5，则直线l与☉O的位置关系是（ ）A. 相交或相切 B. 相交或相离 C. 相切或相离 D. 上三种情况都有可能
如图，在平面直角坐标系中，⊙A与y轴相切于原点O，平行于x轴的直线交⊙A于M、N两点．若点M的坐标是(－4，－2)，则点N的坐标为(　　)A．(－1，－2) B．(1，2)C．(－1.5，－2) D．(1.5，－2)
已知☉O的半径r=7cm,直线l1 // l2,且l1与☉O相切,圆心O到l2的距离为9cm.求l1与l2的距离.
解：（1） l2与l1在圆的同一侧： m=9-7=2 cm
（2）l2与l1在圆的两侧： m=9+7=16 cm
相离:0个;相切：1个;相交：2个
相离:d>r;相切:d=r相交:d0个：相离；1个：相切；2个：相交
d>r：相离;d=r:相切d 转动雨伞时飞出的雨滴，用砂轮磨刀时擦出的火花，都是沿着什么方向飞出的？
都是沿着圆的切线的方向飞出的．
3. 能运用圆的切线的判定定理和性质定理解决问题.
1. 会判定一条直线是否是圆的切线并会过圆上一点作圆的切线.
2. 理解并掌握圆的切线的判定定理及性质定理.
如图，在⊙O中经过半径OA的外端点A作直线l⊥OA,则圆心O到直线 l 的距离是多少？
这时圆心O到直线 l 的距离就是⊙O的半径．
直线 l 和⊙O有什么位置关系?
问题：已知圆O上一点A，怎样根据圆的切线定义过点A作圆O的切线？
观察：（1） 圆心O到直线AB的距离和圆的半径有什么数量关系?（2）二者位置有什么关系？为什么？
经过半径的外端并且垂直于这条半径的直线是圆的切线.
下列各直线是不是圆的切线？如果不是，请说明为什么？
(1)不是，因为没有垂直.
(2),(3)不是，因为没有经过半径的外端点A.
判断一条直线是一个圆的切线有三个方法：
1.定义法：直线和圆只有一个公共点时，我们说这条直线是圆的切线;
2.数量关系法：圆心到这条直线的距离等于半径(即d=r)时，直线与圆相切；
3.判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线.
例1 如图,∠ABC=45°，直线AB是☉O上的直径，点A,且AB=AC.求证：AC是☉O的切线.
分析：直线AC经过半径的一端，因此只要证OA垂直于AB即可.
证明： ∵AB=AC，∠ABC＝45°，
∴∠ACB＝∠ABC＝45°.
∴∠BAC=180°-∠ABC- ∠ACB=90°.
∴ AC是☉O的切线.
通过证明角是90°判断圆的切线
1. 如图 所示，线段 AB 经过圆心 O，交⊙O 于点 A、C，∠BAD＝∠B＝30°，边 BD 交圆于点 D.BD 是⊙O 的切线吗？为什么？
解：BD 是⊙O 的切线．
连接 OD, ∵OD＝OA，∠A＝30°， ∴∠DOB＝60°.
∵∠B＝30°，∴∠ODB＝90°.∴BD 是⊙O 的切线．
例2 已知：直线AB经过⊙O上的点C，并且OA=OB，CA=CB.求证：直线AB是⊙O的切线.
证明：连接OC(如图). ∵ OA＝OB,CA＝CB, ∴ OC是等腰三角形OAB底边AB上的中线.　 ∴ AB⊥OC. ∵ OC是⊙O的半径, ∴ AB是⊙O的切线.
通过证明垂直判断圆的切线
2. 如图,△ABC 中，AB ＝AC ，O 是BC的中点，⊙O 与AB 相切于E. 求证：AC 是⊙O 的切线．
分析：根据切线的判定定理，要证明AC是⊙O的切线，只要证明由点O向AC所作的垂线段OF是⊙O的半径就可以了，而OE是⊙O的半径，因此只需要证明OF=OE.
证明：连接OE ，OA, 过O 作OF ⊥AC.
∵⊙O 与AB 相切于E ， ∴OE ⊥ AB.
又∵△ABC 中，AB ＝AC ，O 是BC 的中点．
∴AO 平分∠BAC，
∵OE 是⊙O 半径，OF ＝OE，OF ⊥ AC.
∴AC 是⊙O 的切线．
又OE ⊥AB ，OF⊥AC.
如图，已知直线AB经过⊙O上的点C，并且OA＝OB，CA＝CB求证：直线AB是⊙O的切线.
如图，OA＝OB=5，AB＝8, ⊙O的直径为6.求证：直线AB是⊙O的切线.
(1) 有交点，连半径,证垂直;(2) 无交点，作垂直,证半径.
证切线时辅助线的添加方法
有切线时常用辅助线添加方法
见切点，连半径，得垂直.
(1)经过圆心且垂直于切线的直线必经过切点;
(2)经过切点且垂直于切线的直线必经过圆心.
思考：如图，如果直线l是⊙O 的切线，点A为切点，那么OA与l垂直吗？
∵直线l是⊙O 的切线，A是切点.
证明：假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M.
则OM 作出小⊙O的同心圆大⊙O，CD切小⊙O于点A,且A点为CD的中点. 连接OA,根据垂径定理，则CD ⊥OA,即圆的切线垂直于经过切点的半径．
利用切线的性质解题时，常需连接辅助线，一般连接圆心与切点，构造直角三角形，再利用直角三角形的相关性质解题.
分析：(1)根据已知条件我们易得∠CAB=∠PAO=90°，由∠P=30°可得出∠AOP=60°，则∠C=30°=∠P，即AC=AP；这样就凑齐了角边角，可证得△ACB≌△APO；
(2)由已知条件可得△AOP为直角三角形，因此可以通过解直角三角形求出半径OA的长.
(1)求证：△ACB≌△APO；
在△ACB和△APO中，∠BAC＝∠OAP，AB＝AO，∠ABO＝∠AOB，∴△ACB≌△APO（ASA）.
证明：∵PA为⊙O的切线，A为切点，
又∵∠P＝30°，∴∠AOB＝60°，又∵OA＝OB，∴△AOB为等边三角形． ∴AB＝AO，∠ABO＝60°.
又∵BC为⊙O的直径，∴∠BAC＝90°.
(2)若AP＝ ，求⊙O的半径．
∴AO＝1，∴CB＝OP＝2，∴OB＝1，即⊙O的半径为1.
3. 如图所示，点 A 是⊙O 外一点，OA 交⊙O 于点 B，AC 是⊙O 的切线，切点是 C，且∠A＝30°，BC＝1.求⊙O 的半径．
解：连接 OC. 因为AC 是⊙O 的切线，所以∠OCA ＝90°. 又∵ ∠A＝30°， ∴ ∠COB＝60° ∴ OBC 是等边三角形． ∴ OB＝BC＝1，即⊙O 的半径为 1.
如图，在⊙O中，AB为直径，AC为弦．过BC延长线上一点G，作GD⊥AO于点D，交AC于点E，交⊙O于点F，M是GE的中点，连接CF、CM．判断CM与⊙O的位置关系，并说明理由；
解：CM与⊙O相切．理由如下：连接OC，如图，∵GD⊥AO于点D，∴∠G+∠GBD=90°，∵AB为直径，∴∠ACB=90°，∵M点为GE的中点，∴MC=MG=ME，∴∠G=∠1，∵OB=OC，∴∠B=∠2，∴∠1+∠2=90°，∴∠OCM=90°，∴OC⊥CM，∴CM为⊙O的切线；
1. 判断下列命题是否正确. ⑴ 经过半径外端的直线是圆的切线. （ ） ⑵ 垂直于半径的直线是圆的切线. （ ） ⑶ 过直径的外端并且垂直于这条直径的直线是圆的切线. （ ） ⑷ 和圆只有一个公共点的直线是圆的切线. （ ） ⑸ 过直径一端点且垂直于直径的直线是圆的切线. （ ）
2. 如图所示，A是☉O上一点，且AO=5, PO=13, AP=12,则PA与☉O的位置关系是 .
3. 如图，在☉O的内接四边形ABCD中，AB是直径，∠BCD=120°，过D点的切线PD与直线AB交于点P，则∠ADP的度数为（ ）A．40° B．35° C．30° D．45°
4.如图, ⊙O切PB于点B,PB=4, PA=2,则⊙O的半径多少？
解：连接OB，则∠OBP=90°.
设⊙O的半径为r,则OA=OB=r, OP=OA+PA=2+r.
OB2+PB2=PO2，即r2+42=(2+r)2.
证明：连接OP. ∵AB=AC,∴∠B=∠C. ∵OB=OP，∴∠B=∠OPB ∴∠OBP=∠C. ∴OP∥AC. ∵PE⊥AC， ∴PE⊥OP. ∴PE为⊙O的切线.
1. 如图,△ABC中，AB=AC，以AB为直径的⊙O交边BC于P， PE⊥AC于E. 求证:PE是⊙O的切线.
2. 如图，O为正方形ABCD对角线AC上一点，以O为圆心，OA长为半径的⊙O与BC相切于点M.求证：CD与⊙O相切．
证明：连接OM，过点O作ON⊥CD于点N，∵⊙O与BC相切于点M，∴OM⊥BC.又∵ON⊥CD，O为正方形ABCD对角线AC上一点，∴OM＝ON，∴CD与⊙O相切．
已知：△ABC内接于☉O，过点A作直线EF.（1）如图1，AB为直径，要使EF为☉O的切线，还需添加的条件是（只需写出两种情况）： ① _________ ；② _____________ .（2）如图2，AB是非直径的弦，∠CAE=∠B，求证：EF是☉O的切线.
证明：连接AO并延长交☉O于D,连接CD,则AD为☉O的直径.∴ ∠D+ ∠DAC=90 °,∵ ∠D与∠B同对 ,∴ ∠D= ∠B,又∵ ∠CAE= ∠B,∴ ∠D= ∠CAE,∴ ∠DAC+ ∠EAC=90°,∴EF是☉O的切线.
经过圆的半径的外端且垂直于这条半径的直线是圆的切线.
证切线时常用辅助线添加方法： ①有公共点，连半径，证垂直；②无公共点，作垂直，证半径.
圆的切线垂直于经过切点的半径
有切线时常用辅助线添加方法： 见切线，连切点，得垂直.
同学们玩过空竹和悠悠球吗？在空竹和悠悠球的旋转的那一瞬间，你能从中抽象出什么样数学图形？
2. 初步学会运用切线长定理进行计算与证明.
1. 掌握切线长的定义及切线长定理.
问题1 上节课我们学习了过圆上一点作已知圆的切线(如左图所示)，如果点P是圆外一点，又怎么作该圆的切线呢？过圆外的一点作圆的切线，可以作几条？
1.切线长的定义： 切线上一点到切点之间的线段的长叫作这点到圆的切线长．
①切线是直线，不能度量.
②切线长是线段的长，这条线段的两个端点分别是圆外一点和切点，可以度量．
2.切线长与切线的区别在哪里？
问题2 PA为☉O的一条切线，沿着直线PO对折，设圆上与点A重合的点为B．
OB是☉O的一条半径吗？
PB是☉O的切线吗？
（利用图形轴对称性解释）
PA、PB有何关系？
∠APO和∠BPO有何关系？
切线长定理 过圆外一点作圆的两条切线，两条切线长相等.圆心与这一点的连线平分两条切线的夹角.
PA、PB分别切☉O于A、B
已知，如图PA、PB是☉O的两条切线，A、B为切点.求证：PA=PB，∠APO=∠BPO.
证明：∵PA切☉O于点A， ∴ OA⊥PA.
同理可得OB⊥PB.
∵OA=OB，OP=OP，
∴Rt△OAP≌Rt△OBP（HL），
∴PA=PB，∠APO=∠BPO.
想一想：若连结两切点A、B，AB交OP于点M.你又能得出什么新的结论?并给出证明.
证明：∵PA，PB是⊙O的切线,点A，B是切点 ∴PA = PB ，∠OPA=∠OPB ∴△PAB是等腰三角形，PM为顶角的平分线 ∴OP垂直平分AB.
想一想：若延长PO交⊙O于点C，连结CA、CB，你又能得出什么新的结论?并给出证明.
证明：∵PA，PB是⊙O的切线,点A，B是切点， ∴PA = PB ，∠OPA=∠OPB. ∴PC=PC. ∴ △PCA ≌ △PCB， ∴AC=BC.
例1 已知：如图，四边形ABCD的边AB、BC、CD、DA与⊙O分别相切于点E、F、G、H.
求证：AB+CD=AD+BC.
证明：∵AB、BC、CD、DA与⊙O分别相切于点E、F、G、H，
∴ AE=AH，BE=BF，CG=CF，DG=DH.
∴ AE+BE+CG+DG=AH+BF+CF+DH.
∴AB+CD=AD+BC.
1. PA、PB是☉O的两条切线，A,B是切点，OA=3.
（1）若AP=4,则OP= ;
（2）若∠BPA=60 °,则OP= .
例2 为了测量一个圆形铁环的半径，某同学采用了如下办法：将铁环平放在水平桌面上，用一个锐角为30°的三角板和一个刻度尺，按如图所示的方法得到相关数据，进而可求得铁环的半径，若三角板与圆相切且测得PA=5cm，求铁环的半径．
分析：欲求半径OP，取圆的圆心为O，连OA、OP，由切线性质知△OPA为直角三角形，从而在Rt△OPA中由勾股定理易求得半径．
切线长定理在生活中的应用
在Rt△OPA中，PA＝5，∠POA＝30°，
解：过O作OQ⊥AB于Q，设铁环的圆心为O，连接OP、OA.
∵AP、AQ为⊙O的切线，∴AO为∠PAQ的平分线，即∠PAO＝∠QAO.
又∠BAC＝60°，∠PAO＋∠QAO＋∠BAC＝180°，∴∠PAO＝∠QAO＝60°.
2. 如图,小敏家厨房一墙角处有一自来水管,装修时为了美观,准备用木板从AB处将水管密封起来,互相垂直的两墙面与水管分别相切于D、E两点,经测量发现AD和BE的长恰是方程x2-25x+150=0的两根(单位:cm),则该自来水管的半径为 cm(AD解析：设圆心为O,连接OD、OE,x2-25x+150=0,(x-10)(x-15)=0,解得:x1=10,x2=15,∵AD 小明在一家木料厂上班，工作之余想对厂里的三角形废料进行加工：裁下一块圆形用料，怎样才能使裁下的圆的面积尽可能大呢？
问题1 如果最大圆存在，它与三角形三边应有怎样的位置关系？
最大的圆与三角形三边都相切
问题2 如何求作一个圆，使它与已知三角形的三边都相切？
(1) 如果半径为r的☉I与△ABC的三边都相切，那么圆心I应满足什么条件？
(2) 在△ABC的内部，如何找到满足条件的圆心I呢？
已知：△ABC.求作：和△ABC的各边都相切的圆.
作法：1.作∠B和∠C的平分线BM和CN，交点为O.2.过点O作OD⊥BC.垂足为D.3.以O为圆心，OD为半径作圆O.
1.与三角形三边都相切的圆叫作三角形的内切圆.
2.三角形内切圆的圆心叫做这个三角形的内心.
3.这个三角形叫做这个圆的外切三角形.
☉I是△ABC的内切圆，点I是△ABC的内心，△ABC是☉I的外切三角形.
例3 已知:△ABC(如图),(1)求作△ABC的内切圆☉I(要求:用尺规作图,保留作图痕迹,写出作法,不要求证明).(2)在题(1)已经作好的图中,若∠BAC=88°,求∠BIC的度数.
解析：(1)①以A为圆心、任意长为半径画圆,分别交AC、AB于点H、G;②分别以H、G为圆心,以大于 HG的长为半径画圆,两圆相交于K点,连接AK,则AK即为∠BAC的平分线;③同理作出∠ABC的平分线BF,交AK于点I,则I即为△ABC内切圆的圆心;④过I作IM⊥BC于M,以I为圆心,IM为半径画圆,则☉I即为所求圆.
(2)∵∠BAC=88°,∴∠ABC+∠ACB=180°-88°=92°,∴∠IBC+∠ICB= (∠ABC+∠ACB)= ×92°=46°,∴∠BIC=180°-46°=134°.
3. △ABC的内切圆半径为r， △ABC的周长为l，求△ABC的面积.（提示：设内心为O，连接OA、OB、OC.）
解： 设AB = c，BC = a，AC = b.
则S△OBC= ar, S△OBA= cr, S△OAC= br,
S△ABC=S△OBC +S△OBA +S△OAC= ar + cr + br= r（a+c+b）= lr
问题1 如图，☉I是△ABC的内切圆，那么线段IA，IB ,IC有什么特点？
三角形的内心的定义和性质
问题2 如图，分别过点作AB、AC、BC的垂线，垂足分别为E、F，G，那么线段IE、IF、IG之间有什么关系？
三角形的内心在三角形的角平分线上.
三角形的内心到三角形的三边距离相等.
IA，IB，IC是△ABC的角平分线，IE=IF=IG.
例4 如图，△ABC中，∠ B=43°，∠C=61 °，点I是△ABC的内心，求∠ BIC的度数.
∵点I是△ABC的内心，
∴IB，IC分别是∠ B，∠C的平分线，
利用三角形内心的性质求角度
4.如图,在△ABC中,点P是△ABC的内心,则∠PBC+∠PCA+∠PAB= .
解析：∵点P是△ABC的内心,∴PB平分∠ABC,PA平分∠BAC,PC平分∠ACB,∴∠PBC+∠PCA+∠PAB=90°.
三角形三边中垂线的交点
1.OA=OB=OC2.外心不一定在三角形的内部．
三角形三条角平分线的交点
1.到三边的距离相等；2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB3.内心在三角形内部．
1.如图，一把直尺，60°的直角三角板和光盘如图摆放，A为60°角与直尺交点，AB=3，则光盘的直径是（　　）A．3 B．C．6 D．
解析：设三角板与圆的切点为C，连接OA、OB，由切线长定理知AB=AC=3，OA平分∠BAC，∴∠OAB=60°，在Rt△ABO中，OB=ABtan∠OAB= ，∴光盘的直径为 ．
2.如图，菱形ABOC的边AB、AC分别与⊙O相切于点D、E．若点D是AB的中点，则∠DOE= ．
解析：连接OA，∵四边形ABOC是菱形，∴BA=BO，∵AB与⊙O相切于点D，∴OD⊥AB，∵点D是AB的中点，∴直线OD是线段AB的垂直平分线，∴OA=OB，∴△AOB是等边三角形，∵AB与⊙O相切于点D，∴OD⊥AB，∴∠AOD= ∠AOB=30°，同理，∠AOE=30°，∴∠DOE=∠AOD+∠AOE= 60° ．
（3）若∠BIC=100 °，则∠A = 度.
（2）若∠A=80 °，则∠BIC = 度.
3.如图，在△ABC中，点I是内心， （1）若∠ABC=50°， ∠ACB=70°，∠BIC=_____.
（4）试探索： ∠A与∠BIC之间存在怎样的数量关系？
如图所示，已知在△ABC中，∠B＝90°，O是AB上一点，以O为圆心，OB为半径的圆与AB交于E，与AC相切于点D.求证：DE∥OC.
证明：连接OD，∵AC切⊙O于点D，∴OD⊥AC，∴∠ODC=∠B=90°.在Rt△OCD和Rt△OCB中，OD＝OB ，OC＝OC ∴Rt△ODC≌Rt△OBC（HL），∴∠DOC=∠BOC.∵OD=OE，∴∠ODE=∠OED，∵∠DOB=∠ODE+∠OED，
∴∠BOC=∠OED，∴DE∥OC．
如图，△ABC中，I是内心，∠A的平分线和△ABC的外接圆相交于点D.求证：DI＝DB.
证明：连接BI.∵I是△ABC的内心，∴∠BAD=∠CAD，∠ABI=∠CBI，∵∠CBD=∠CAD，∴∠BAD=∠CBD，∵∠BID=∠BAD+∠ABI，∠IBD=∠CBI+∠CBD，∴∠BID=∠IBD，∴BD=ID．
提供了证线段和角相等的新方法
分别连接圆心和切点；连接两切点；连接圆心和圆外一点.
运用切线长定理，将相等线段转化集中到某条边上，从而建立方程.