八年级上册12.2 三角形全等的判定导学案

这是一份八年级上册12.2 三角形全等的判定导学案，共11页。
：全等三角形的判定





例1：已知：如图，OP是∠AOC和∠BOD的平分线，OA=OC，OB=OD.求证：AB=CD.





证明：∵OP是∠AOC和∠BOD的平分线，


∴∠AOP=∠COP，∠BOP=∠DOP． ∴∠AOB=∠COD．


在△AOB和△COD中，





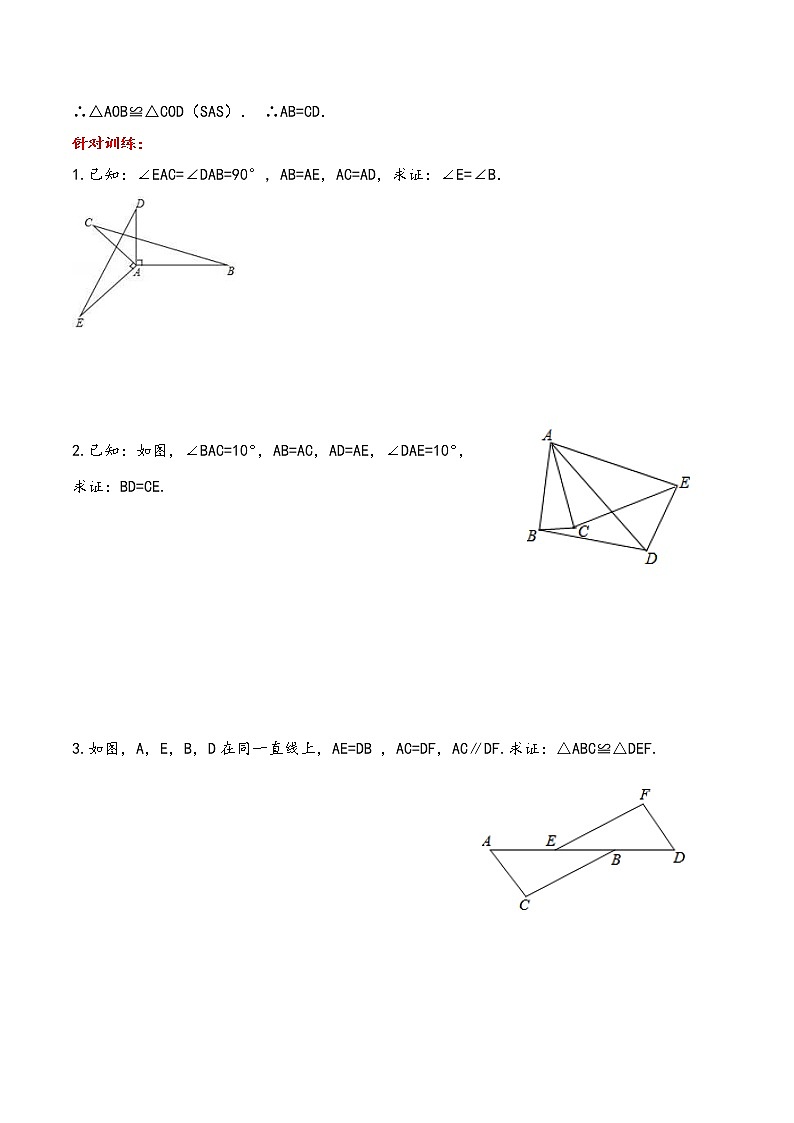
∴△AOB≌△COD（SAS）． ∴AB=CD．


针对训练：


1.已知：∠EAC=∠DAB=90°，AB=AE，AC=AD，求证：∠E=∠B．














2.已知：如图，∠BAC=10，AB=AC，AD=AE，∠DAE=10，


求证：BD=CE.

















3.如图，A，E，B，D在同一直线上，AE=DB，AC=DF，AC∥DF.求证：△ABC≌△DEF.











例2：如图，点A、C、D、B四点共线，且AC=BD，∠A=∠B，∠ADE=∠BCF.求证：DE=CF.





证明：AC=BD，


AC+CD=BD+CD，AD=BC


在△AED和△BFC中，





△AED≌△BFC（ASA）


DE=CF.





针对训练：


1.如图，BD⊥AC于点D，CE⊥AB于点E，AD=AE，求证：BE=CD.





























例3：如图，点B、E、C、F在同一条直线上，BE=CF，AB=DE，AC=DF，求证：△ABC≌△DEF.





证明：BE=CF，EF=BC.


在△ABC和△DEF中，





△ABC≌△DEF（SSS）


∠B=∠DEF，AB∥DE.





针对训练：


1.一个平分角的仪器如图所示，其中AB=AD，BC=DC.求证：∠BAC=∠DAC.





























例4：已知，如图，D是△ABC 的边AB上一点，DF交AC于点 E，DE=FE，FC∥AB.


求证：AD=CF.





证明：FC∥AB，∠A=∠ECF，∠ADE=∠F.


在△ADE和△CFE中，





△ADE≌△CFE（AAS）


AD=CF.





针对训练：


1.如图，点F、C在BE上，BF=CE，∠A=∠D，∠B=∠E． 求证：AB=DE．





2.如图，点D是AB上一点，DF交AC于点E，DE=FE，FC∥AB，求证：AE=CE.





例5：如图，在直角三角形ABC中，∠C=90，AB=12cm，BC=6cm，PQ=AB，P、Q两点分别在线段AC和AC的垂线AX上移动，则当AP等于多少时，才能使△ABC和△APQ全等?





解析：∠C=∠QAP=90，△ABC与△QPA都是直角三角形.


在Rt△ABC与Rt△QPA中，斜边AB=QP，由“HL”可知，要使Rt△ABC≌Rt△QPA，只需要满足AP=BC或AP=AC即可，AP=6cm或12cm.





针对训练：


1.如图所示，AD、BC相交于点O，AD=BC，∠C=∠D=90.


求证：△ACB≌△BDA；


若∠ABC=35，则∠CAO=_____.











例6：如图，把手机放在一个支架上面，就可以非常方便地使用，这是因为手机支架利用了三角形的 （ ）





三角形的稳定性 B.两点之间线段最短 C.两点确定一条直线 D.垂线段最短


基础练习


如图，要利用“SAS”说明△ABD≌△ACD，需添加的条件是.





第1题图 第2题图 第3题图


2.如图所示，∠C=∠D=90°，可使用“HL”判定Rt△ABC与Rt△ABD全等，则应添加一个条件是 ．


3.如图，某同学把一块三角形的玻璃打破成了三块，现要到玻璃店去配一块大小、形状完全相同的玻璃，那么他可以带 （ ）


A.① B.② C.③ D.①和②


如图，△ABC中，AB=AC，EB=EC，则由“SSS”可以判定 （）


△ABD≌△ACD B.△ABE≌△ACE


C.△BDE≌△CD E D.以上答案都不对





第4题图 第5题图 第6题图


5.如图，工人师傅做了一个长方形窗框AB-CD，E、F、G、H分别是四条边上的中点，为了使它稳固，需要在窗框上钉一根木条，这根木条不应钉在 （ ）


A. A、C两点之间 B.E、G 两点之间 C.B、F两点之间 D.G、H 两点之间


6.如图，OP是∠AOB的平分线，点C，D分别在角的两边OA，OB上，添加下列条件，不能判定△POC≌△POD的选项是 （ ）


A.PC⊥OA，PD⊥OB B.OC=OD C.∠OPC=∠OPD D.PC=PD








强化训练


如图，△ABC中，AB=AC，AD是角平分线，BE=CF，则下列说法:(1)DA平分∠EDF；(2)△EBD≌△FCD；(3)△AED≌△AFD；(4)AD⊥BC.正确的有 （ ）





A. 1个 B. 2个 C. 3个 D. 4个


2.如图，、b、c分别表示△ABC的三边长，下面与△ABC全等的三角形是 （ ）





3.如图，已知点P是线段AB上一点，∠ACB=∠ADB，在下面判断中错误的是 （ ）


A.若添加条件AC=AD，则△APC≌△APD


B.若添加条件BC=BD，则△APC≌△APD


C.若添加条件∠ACB=∠ADB，则△APC≌△APD


D.若添加条件∠CAB=∠DAB，则△APC≌△APD





第3题图 第4题图 第5题图


4.如图，已知∠ABC=∠BAD，添加下列条件还不能判定△ABC≌△BAD的是 （ ）


A.AC=BD B.∠CAB=∠DBA C.∠C=∠D D.BC=AD


5.如图，在△ABC和△BDE中，点C在边BD上，边AC交边BE于点F.若AC=BD，AB=ED，BC=BE，则∠ACB等于 （ ）


A.∠EDB B.∠BED C.∠AFB D.2∠ABF





6.如图所示，△ABC是不等边三角形，DE＝BC，以D、E为两个顶点作位置不同的三角形，使所作的三角形与△ABC全等，这样的三角形最多可以作出个.





第6题图 第7题图


7.如图，四边形ABCD的对角线AC、BD相交于点O，△ABO≌△ADO.下列结论：①AC⊥BD；②CB=CD；③△ABC≌△ADC；④DA=DC.其中所有正确结论的序号是_____ .


8.如图，OP平分∠MON，PE⊥OM于E，PF⊥ON于F，OA=OB，则图中有_____对全等三角形.





9.如图，已知∠DCE＝90°，∠DAC＝90°，EB⊥AC于B，且DC＝EC，能否在△BCE中找出与AB＋AD相等的线段，并说明理由.








10.如图，在△ABC中，∠ACB=90，AC=BC，BE⊥CE于E，AD⊥CE于D.


(1)求证：△ADC≌△CEB；


(2)若AD=5cm，DE=3cm，求BE的长度.





11.如图，在四边形ABCD中，AD=BC，BE=DF，AE⊥BD，CF⊥BD，垂足分别为E、F.


（1）求证：△ADE≌△CBF；


（2）若AC与BD相交于点O，求证：AO=CO.











12.课间，小明拿着老师的等腰直角三角板玩，不小心掉到两墙之间，如图，求证：△ADC≌△CEB.











13.如图，点B，F，C，E在直线上（F，C之间不能直接测量），点A，D在异侧，测得AB=DE，AC=DF，BF=EC.


（1）求证：△ABC≌△DEF；


（2）指出图中所有平行的线段，并说明理由.

















能力提升


1.已知△ABN和△ACM位置如图所示，AB=AC，AD=AE，∠1=∠2.


（1）求证：BD=CE；


（2）求证：∠M=∠N.





2.如图（1）所示，A、E、F、C在同一条直线上，AE=CF，过E、F分别作DE⊥AC，BF⊥AC，若AB=CD.


（1）问BD平分EF吗？说明理由.


（2）若将△DEC的边EC沿AC方向移动变为图（2）时，其余条件不变，上述结论是否成立.请说明理由.





























►知识点拨：


1.判定两个三角形全等的基本事实---“边角边”


两边和它们的夹角相等的两个三角形全等.（SAS）


2.判定两个三角形全等的基本事实--“角边角”


两角和它们的夹边对应相等的两个三角形全等.（ASA）


3.判定两个三角形全等的基本事实--“边边边”


三边分别相等的两个三角形全等.（SSS）


4.判定两个三角形全等的基本事实--“角角边”


两角分别相等且其中一组对边相等的两个三角形全等.（AAS）


5.判定两个三角形全等的基本事实--“斜边、直角边”


斜边和一条直角边分别相等的两个直角三角形全等.（HL）


注意：①“HL”只适用于直角三角形；②斜边和其中一直角边对应相等；③三角形全等的判定方法对直角三角形全部适用.


6.三角形的稳定性：确定三角形的三边，这个三角形的大小和形状就完全确定，这个性质叫三角形的稳定性.三角形稳定性依据的是“边边边”.