

还剩13页未读,
继续阅读
2019-2020学年安徽省铜陵市七年级(下)期末数学试卷 解析版
展开
2019-2020学年安徽省铜陵市七年级(下)期末数学试卷
一、选择题(本大题10小题,共30分)
1.(3分)下列语句是命题的是( )
A.你有橡皮擦吗 B.小华是男生
C.垃圾要分类 D.出门戴口罩
2.(3分)的算术平方根是( )
A.4 B.±4 C.2 D.±2
3.(3分)已知点P(m+2,2m﹣4)在x轴上,则点P的坐标是( )
A.(4,0) B.(0,4) C.(﹣4,0) D.(0,﹣4)
4.(3分)2020年5月20日,随着第一批考生经体温检测等流程后进入考点,铜陵市2020年初中学业水平体育考试正式拉开序幕.据了解,铜陵市共有1.7万名考生报名参加体育考试,为了了解考生体育成绩,从中抽取2000名考生的体育成绩进行统计,在这个问题中样本是( )
A.1.7万名考生 B.2000名考生
C.1.7万名考生体育成绩 D.2000名考生的体育成绩
5.(3分)如图,直线a∥b,∠1=50°,∠2=30°,则∠3的度数为( )
A.40° B.90° C.50° D.100°
6.(3分)若8xmy与6x3yn的和是单项式,则(m+n)3的平方根为( )
A.4 B.8 C.±4 D.±8
7.(3分)如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为( )
A.北偏东30° B.北偏东80° C.北偏西30° D.北偏西50°
8.(3分)下列说法正确的是( )
A.直线外一点到这条直线的垂线叫做点到直线的距离
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.同旁内角互补是真命题
D.经过一点,有且只有一条直线与这条直线平行
9.(3分)已知x=2是不等式(x﹣5)(ax﹣3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是( )
A.a>1 B.a≤2 C.1<a≤2 D.1≤a≤2
10.(3分)小慧去花店购买鲜花,若买5支玫瑰和3支百合,则她所带的钱还剩下10元;若买3支玫瑰和5支百合,则她所带的钱还缺4元.若只买8支玫瑰,则她所带的钱还剩下( )
A.31元 B.30元 C.25元 D.19元
二、填空题(本大题6小题,每小题3分,共18分)
11.(3分)不等式2x+3>3x的解集为 .
12.(3分)在第二象限,到x轴距离为4,到y轴距离为3的点P的坐标是 .
13.(3分)在平面直角坐标系中,三角形ABC的三个顶点的坐标分别是A(2,3),B(0,4),C(0,﹣2),则三角形ABC的面积为 .
14.(3分)把一根9m长的钢管截成1m长和2m长两种规格均有的短钢管,且没有余料,设某种截法中1m长的钢管有a根,则a的值可能有 种.
15.(3分)如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(﹣1,0),(0,),现将该三角板向右平移使点A与点O重合,得到△OCB',再△OCB′绕O点顺时针旋转90°得到△OC′B″将则点B的对应点B″的坐标是 .
16.(3分)小华在文具超市挑选了6支中性笔和5本笔记本.结账时,小华付款50元,营业店员找零4元,小华说:“阿姨您好,6支中性笔和5本笔记本一共42元,应该找零8元.”店员说:“啊…哦,我明白了,小朋友你真棒,我刚才把中性笔和笔记本的单价弄反了,对不起,再找给你4元”.根据两人的对话计算:若购买一支中性笔和一本笔记本一共需要付款 元.
三、计算题(本大题4小题,每小题7分,共28分)
17.(7分)计算:(﹣1)2020﹣(+)+.
18.(7分)解方程组:.
19.(7分)解不等式组:,并将解集在数轴上表示出来.
20.(7分)已知关于x,y的二元一次方程组的解互为相反数,求k的值.
四、解答题(本大题3小题,每小题8分,共24分)
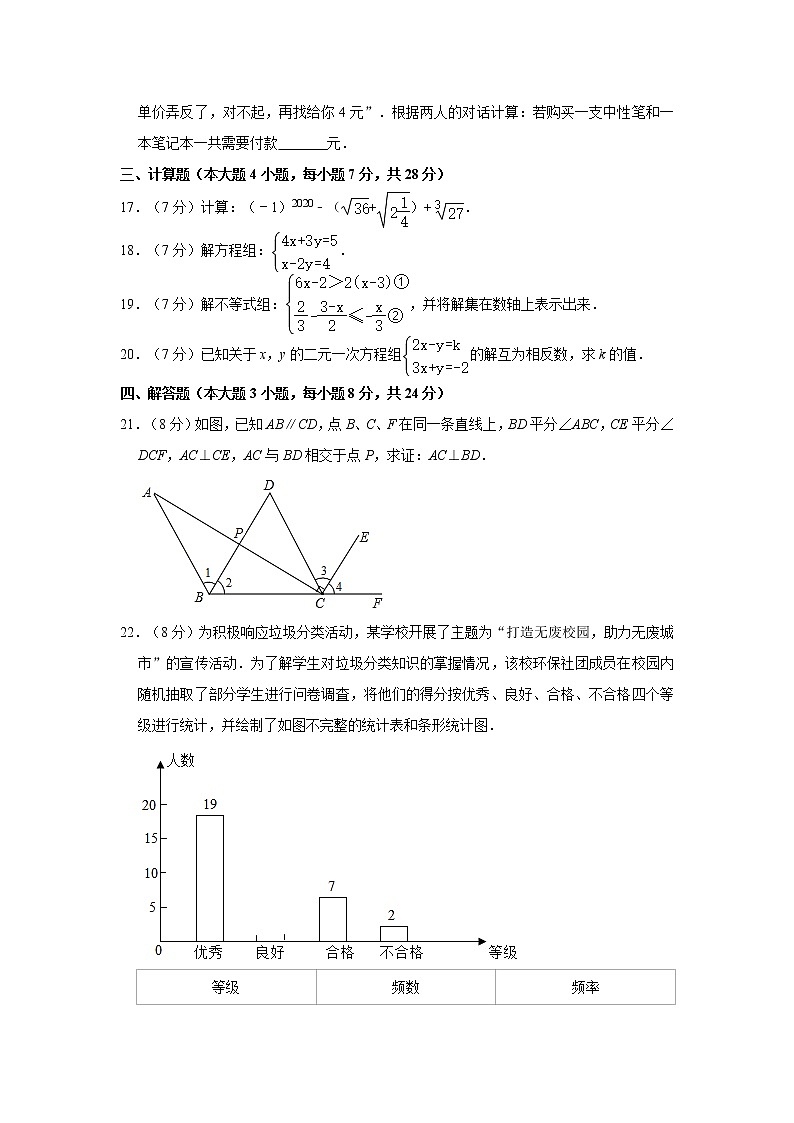
21.(8分)如图,已知AB∥CD,点B、C、F在同一条直线上,BD平分∠ABC,CE平分∠DCF,AC⊥CE,AC与BD相交于点P,求证:AC⊥BD.
22.(8分)为积极响应垃圾分类活动,某学校开展了主题为“打造无废校园,助力无废城市”的宣传活动.为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调査,将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如图不完整的统计表和条形统计图.
等级
频数
频率
优秀
19
38%
良好
m
44%
合格
7
n%
不合格
2
4%
(1)本次调查随机抽取了 名学生;表中m= ,n= ;
(2)补全条形统计图;
(3)垃圾分类节约资源,还地球一个碧海蓝天,写一句关于垃圾分类的宣传标语,要求20字以内;
(4)若全校有1500名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人?
23.(8分)某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共12辆.若购买A型公交车1辆、B型公交车2辆,共需440万元;若购买A型公交车2辆、B型公交车1辆,共需400万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为64万人次和120万人次.若该公司购买A型和B型公交车的总费用不超过1660万元,且确保这12辆公交车在该线路的年均载客量总和不少于910万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
2019-2020学年安徽省铜陵市七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本大题10小题,共30分)
1.(3分)下列语句是命题的是( )
A.你有橡皮擦吗 B.小华是男生
C.垃圾要分类 D.出门戴口罩
【分析】根据命题的定义分别进行判断.
【解答】解:垃圾要分类和出门戴口罩都是描叙性语言,它们都不是命题;“你有橡皮擦吗?”是疑问句,它不是命题;小华是男生是命题.
故选:B.
2.(3分)的算术平方根是( )
A.4 B.±4 C.2 D.±2
【分析】先计算的值,再根据算术平方根的定义求解.
【解答】解:=4,
4的算术平方根2,
故选:C.
3.(3分)已知点P(m+2,2m﹣4)在x轴上,则点P的坐标是( )
A.(4,0) B.(0,4) C.(﹣4,0) D.(0,﹣4)
【分析】直接利用关于x轴上点的坐标特点得出m的值,进而得出答案.
【解答】解:∵点P(m+2,2m﹣4)在x轴上,
∴2m﹣4=0,
解得:m=2,
∴m+2=4,
则点P的坐标是:(4,0).
故选:A.
4.(3分)2020年5月20日,随着第一批考生经体温检测等流程后进入考点,铜陵市2020年初中学业水平体育考试正式拉开序幕.据了解,铜陵市共有1.7万名考生报名参加体育考试,为了了解考生体育成绩,从中抽取2000名考生的体育成绩进行统计,在这个问题中样本是( )
A.1.7万名考生 B.2000名考生
C.1.7万名考生体育成绩 D.2000名考生的体育成绩
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【解答】解:在这个问题中样本是2000名考生的体育成绩.
故选:D.
5.(3分)如图,直线a∥b,∠1=50°,∠2=30°,则∠3的度数为( )
A.40° B.90° C.50° D.100°
【分析】由平行线的性质得∠1=∠4=50°,根据平角的定义和角的和差求得∠3的度数为100°.
【解答】解:如图所示:
∵a∥b,
∴∠1=∠4,
又∵∠1=50°,
∴∠4=50°,
又∵∠2+∠3+∠4=180°,∠2=30°,
∴∠3=100°,
故选:D.
6.(3分)若8xmy与6x3yn的和是单项式,则(m+n)3的平方根为( )
A.4 B.8 C.±4 D.±8
【分析】根据单项式的和是单项式,可得同类项,根据同类项是字母项相同且相同字母的指数也相同,可得m、n的值,再代入计算可得答案.
【解答】解:由8xmy与6x3yn的和是单项式,得
m=3,n=1.
(m+n)3=(3+1)3=64,64的平方根为±8.
故选:D.
7.(3分)如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为( )
A.北偏东30° B.北偏东80° C.北偏西30° D.北偏西50°
【分析】根据平行线的性质,可得∠2,根据角的和差,可得答案.
【解答】解:如图,
AP∥BC,
∴∠2=∠1=50°.
∠3=∠4﹣∠2=80°﹣50°=30°,
此时的航行方向为北偏东30°,
故选:A.
8.(3分)下列说法正确的是( )
A.直线外一点到这条直线的垂线叫做点到直线的距离
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.同旁内角互补是真命题
D.经过一点,有且只有一条直线与这条直线平行
【分析】利用点到直线的距离的定义、平行线的性质及平行公理对每个选项进行判断后即可确定正确的选项.
【解答】解:A、直线外一点到这条直线的垂线段的长度叫做点到直线的距离,故原命题错误,不符合题意;
B、符合垂直的性质,正确,符合题意;
C、两直线平行,同旁内角互补,故原命题错误,不符合题意;
D、经过直线外一点,有且只有一条直线与这条直线平行,故原命题错误,不符合题意;
故选:B.
9.(3分)已知x=2是不等式(x﹣5)(ax﹣3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是( )
A.a>1 B.a≤2 C.1<a≤2 D.1≤a≤2
【分析】根据x=2是不等式(x﹣5)(ax﹣3a+2)≤0的解,且x=1不是这个不等式的解,列出不等式,求出解集,即可解答.
【解答】解:∵x=2是不等式(x﹣5)(ax﹣3a+2)≤0的解,
∴(2﹣5)(2a﹣3a+2)≤0,
解得:a≤2,
∵x=1不是这个不等式的解,
∴(1﹣5)(a﹣3a+2)>0,
解得:a>1,
∴1<a≤2,
故选:C.
10.(3分)小慧去花店购买鲜花,若买5支玫瑰和3支百合,则她所带的钱还剩下10元;若买3支玫瑰和5支百合,则她所带的钱还缺4元.若只买8支玫瑰,则她所带的钱还剩下( )
A.31元 B.30元 C.25元 D.19元
【分析】设每支玫瑰x元,每支百合y元,根据总价=单价×数量结合小慧带的钱数不变,可得出关于x,y的二元一次方程,整理后可得出y=x+7,再将其代入5x+3y+10﹣8x中即可求出结论.
【解答】解:设每支玫瑰x元,每支百合y元,
依题意,得:5x+3y+10=3x+5y﹣4,
∴y=x+7,
∴5x+3y+10﹣8x=5x+3(x+7)+10﹣8x=31.
故选:A.
二、填空题(本大题6小题,每小题3分,共18分)
11.(3分)不等式2x+3>3x的解集为 x<3 .
【分析】移项、合并同类项,系数化为1即可求出不等式的解集.
【解答】解:2x+3>3x,
移项得:2x﹣3x>﹣3,
合并得:﹣x>﹣3,
系数化为1得:x<3.
故答案为x<3.
12.(3分)在第二象限,到x轴距离为4,到y轴距离为3的点P的坐标是 (﹣3,4) .
【分析】应先判断出点P的横、纵坐标的符号,进而根据到坐标轴的距离判断点P的具体坐标.
【解答】解:∵P在第二象限,
∴点P的横坐标小于0,纵坐标大于0;
又∵点P到x轴的距离是4,即点P的纵坐标为4;点P到y轴的距离为3,即点P的横坐标为﹣3,
∴点P的坐标是(﹣3,4);
故答案是:(﹣3,4).
13.(3分)在平面直角坐标系中,三角形ABC的三个顶点的坐标分别是A(2,3),B(0,4),C(0,﹣2),则三角形ABC的面积为 2 .
【分析】直接利用三角形的面积公式解答.
【解答】解:如图,BC=4+2=6.
所以S△ABC=BC•xA==6.
故答案是:2.
14.(3分)把一根9m长的钢管截成1m长和2m长两种规格均有的短钢管,且没有余料,设某种截法中1m长的钢管有a根,则a的值可能有 4 种.
【分析】设某种截法中1m长的钢管有a根,2m长的钢管有b根,根据两种规格钢管的总长度为9m,即可得出关于a,b的二元一次方程,结合a,b均为正整数,即可找出各种截法,进而可得出结论.
【解答】解:设某种截法中1m长的钢管有a根,2m长的钢管有b根,
依题意,得:a+2b=9,
∴a=9﹣2b.
∵a,b均为正整数,
∴当b=1时,a=7;当b=2时,a=5;当b=3时,a=3;当b=4时,a=1,
∴a的值可能有4种.
故答案为:4.
15.(3分)如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(﹣1,0),(0,),现将该三角板向右平移使点A与点O重合,得到△OCB',再△OCB′绕O点顺时针旋转90°得到△OC′B″将则点B的对应点B″的坐标是 (,﹣1) .
【分析】如图,由题意B′(1,).
【解答】解:如图,由题意B′(1,).
∵△OCB′≌△OC′B″,
∴OC=OC′=1,C′B″=CB′=,
∴B″(,﹣1).
故答案为(,﹣1).
16.(3分)小华在文具超市挑选了6支中性笔和5本笔记本.结账时,小华付款50元,营业店员找零4元,小华说:“阿姨您好,6支中性笔和5本笔记本一共42元,应该找零8元.”店员说:“啊…哦,我明白了,小朋友你真棒,我刚才把中性笔和笔记本的单价弄反了,对不起,再找给你4元”.根据两人的对话计算:若购买一支中性笔和一本笔记本一共需要付款 8 元.
【分析】设购买一支中性笔x元,购买一本笔记本y元,根据“6支中性笔和5本笔记本一共42元”、“5支中性笔和6本笔记本一共46元”列出方程组并解答.
【解答】解:设购买一支中性笔x元,购买一本笔记本y元,则.
由①+②,得11(x+y)=88.
所以x+y=8.
即:购买一支中性笔和一本笔记本一共需要付款8元.
故答案是:8.
三、计算题(本大题4小题,每小题7分,共28分)
17.(7分)计算:(﹣1)2020﹣(+)+.
【分析】原式利用乘方的意义,平方根、立方根性质计算即可求出值.
【解答】解:原式=1﹣(6+)+3
=1﹣7+3
=﹣3.
18.(7分)解方程组:.
【分析】方程组利用加减消元法求出解即可.
【解答】解:,
①﹣②×4得:11y=﹣11,即y=﹣1,
把y=﹣1代入②得:x=2,
则方程组的解为.
19.(7分)解不等式组:,并将解集在数轴上表示出来.
【分析】先求出每个不等式的解集,再求出不等式组的解集,最后在数轴上表示出来即可.
【解答】解:,
解不等式①得:x>﹣1,
解不等式②得:x≤1,
∴不等式组的解集为﹣1<x≤1,
在数轴上表示为:
.
20.(7分)已知关于x,y的二元一次方程组的解互为相反数,求k的值.
【分析】用含k的代数式表示x和y,根据方程组的解互为相反数可得x+y=0,列出关于k的方程,进而可得k的值.
【解答】解:∵方程组的解互为相反数,
∴x+y=0,
∴
∴②﹣①得,2x=﹣2,
∴x=﹣1,
∴y=1,
把x=﹣1,y=1代入2x﹣y=k中,
∴2×(﹣1)﹣1=k,
∴k=﹣3.
答:k的值为﹣3.
四、解答题(本大题3小题,每小题8分,共24分)
21.(8分)如图,已知AB∥CD,点B、C、F在同一条直线上,BD平分∠ABC,CE平分∠DCF,AC⊥CE,AC与BD相交于点P,求证:AC⊥BD.
【分析】根据平行线的性质可以得到∠1、∠2、∠3、∠4之间的关系,再根据AC⊥CE,即可得到∠4+∠PCB=90°,然后即可得到∠2+∠PCB=90°,从而可以得到结论成立.
【解答】证明:∵AB∥CD,
∴∠ABC=∠DCF,
∵BD平分∠ABC,CE平分∠DCF,
∴∠1=∠2=∠3=∠4,
∵AC⊥CE,
∴∠4+∠PCB=90°,
∴∠2+∠PCB=90°,
∴∠BPC=90°,
∴AC⊥BD.
22.(8分)为积极响应垃圾分类活动,某学校开展了主题为“打造无废校园,助力无废城市”的宣传活动.为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调査,将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如图不完整的统计表和条形统计图.
等级
频数
频率
优秀
19
38%
良好
m
44%
合格
7
n%
不合格
2
4%
(1)本次调查随机抽取了 50 名学生;表中m= 22 ,n= 14 ;
(2)补全条形统计图;
(3)垃圾分类节约资源,还地球一个碧海蓝天,写一句关于垃圾分类的宣传标语,要求20字以内;
(4)若全校有1500名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人?
【分析】(1)用优秀的人数除以优秀的人数所占的百分比即可得到抽查的人数,然后即可计算出m、n的值;
(2)根据(1)中m的值,可以将条形统计图补充完整;
(3)本题答案不唯一,只要合理即可;
(4)根据频数分布表中的数据,即可计算出该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
【解答】解:(1)本次调查随机抽取了19÷38%=50名学生,
m=50×44%=22,n%=×100%=14%,
故答案为:50,22,14;
(2)由(1)知,m=22,
补全的条形统计图如右图所示;
(3)如果你能做好垃圾分类,那么地球就会给你一个碧海蓝天;
(4)1500×(38%+44%)=1230(人),
答:该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有1230人.
23.(8分)某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共12辆.若购买A型公交车1辆、B型公交车2辆,共需440万元;若购买A型公交车2辆、B型公交车1辆,共需400万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为64万人次和120万人次.若该公司购买A型和B型公交车的总费用不超过1660万元,且确保这12辆公交车在该线路的年均载客量总和不少于910万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
【分析】(1)设购买A型公交车每辆需要x万元,购买B型公交车每辆需要y万元,根据“若购买A型公交车1辆、B型公交车2辆,共需440万元;若购买A型公交车2辆、B型公交车1辆,共需400万元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买m辆A型公交车,则购买(12﹣m)辆B型公交车,根据“购买A型和B型公交车的总费用不超过1660万元,且确保这12辆公交车在该线路的年均载客量总和不少于910万人次”,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,再结合m为正整数即可得出各购车方案,设购车总费用为w万元,利用总价=单价×数量,即可得出w关于m的函数关系式,利用一次函数的性质即可解决最值问题.
【解答】解:(1)设购买A型公交车每辆需要x万元,购买B型公交车每辆需要y万元,
依题意,得:,
解得:.
答:购买A型公交车每辆需要120万元,购买B型公交车每辆需要160万元.
(2)设购买m辆A型公交车,则购买(12﹣m)辆B型公交车,
依题意,得:,
解得:6≤m≤9.
又∵m为正整数,
∴m可以为7,8,9,
∴该公司有3种购车方案,方案1:购买7辆A型公交车,5辆B型公交车;方案2:购买8辆A型公交车,4辆B型公交车;方案3:购买9辆A型公交车,3辆B型公交车.
设购车总费用为w万元,则w=120m+160(12﹣m)=﹣40m+1920,
∵k=﹣40<0,
∴w随m的增大而减小,
∴当m=9时,w取得最小值,最小值=﹣40×9+1920=1560,
∴方案3购买9辆A型公交车,3辆B型公交车总费用最少,最少总费用为1560万元.
一、选择题(本大题10小题,共30分)
1.(3分)下列语句是命题的是( )
A.你有橡皮擦吗 B.小华是男生
C.垃圾要分类 D.出门戴口罩
2.(3分)的算术平方根是( )
A.4 B.±4 C.2 D.±2
3.(3分)已知点P(m+2,2m﹣4)在x轴上,则点P的坐标是( )
A.(4,0) B.(0,4) C.(﹣4,0) D.(0,﹣4)
4.(3分)2020年5月20日,随着第一批考生经体温检测等流程后进入考点,铜陵市2020年初中学业水平体育考试正式拉开序幕.据了解,铜陵市共有1.7万名考生报名参加体育考试,为了了解考生体育成绩,从中抽取2000名考生的体育成绩进行统计,在这个问题中样本是( )
A.1.7万名考生 B.2000名考生
C.1.7万名考生体育成绩 D.2000名考生的体育成绩
5.(3分)如图,直线a∥b,∠1=50°,∠2=30°,则∠3的度数为( )
A.40° B.90° C.50° D.100°
6.(3分)若8xmy与6x3yn的和是单项式,则(m+n)3的平方根为( )
A.4 B.8 C.±4 D.±8
7.(3分)如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为( )
A.北偏东30° B.北偏东80° C.北偏西30° D.北偏西50°
8.(3分)下列说法正确的是( )
A.直线外一点到这条直线的垂线叫做点到直线的距离
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.同旁内角互补是真命题
D.经过一点,有且只有一条直线与这条直线平行
9.(3分)已知x=2是不等式(x﹣5)(ax﹣3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是( )
A.a>1 B.a≤2 C.1<a≤2 D.1≤a≤2
10.(3分)小慧去花店购买鲜花,若买5支玫瑰和3支百合,则她所带的钱还剩下10元;若买3支玫瑰和5支百合,则她所带的钱还缺4元.若只买8支玫瑰,则她所带的钱还剩下( )
A.31元 B.30元 C.25元 D.19元
二、填空题(本大题6小题,每小题3分,共18分)
11.(3分)不等式2x+3>3x的解集为 .
12.(3分)在第二象限,到x轴距离为4,到y轴距离为3的点P的坐标是 .
13.(3分)在平面直角坐标系中,三角形ABC的三个顶点的坐标分别是A(2,3),B(0,4),C(0,﹣2),则三角形ABC的面积为 .
14.(3分)把一根9m长的钢管截成1m长和2m长两种规格均有的短钢管,且没有余料,设某种截法中1m长的钢管有a根,则a的值可能有 种.
15.(3分)如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(﹣1,0),(0,),现将该三角板向右平移使点A与点O重合,得到△OCB',再△OCB′绕O点顺时针旋转90°得到△OC′B″将则点B的对应点B″的坐标是 .
16.(3分)小华在文具超市挑选了6支中性笔和5本笔记本.结账时,小华付款50元,营业店员找零4元,小华说:“阿姨您好,6支中性笔和5本笔记本一共42元,应该找零8元.”店员说:“啊…哦,我明白了,小朋友你真棒,我刚才把中性笔和笔记本的单价弄反了,对不起,再找给你4元”.根据两人的对话计算:若购买一支中性笔和一本笔记本一共需要付款 元.
三、计算题(本大题4小题,每小题7分,共28分)
17.(7分)计算:(﹣1)2020﹣(+)+.
18.(7分)解方程组:.
19.(7分)解不等式组:,并将解集在数轴上表示出来.
20.(7分)已知关于x,y的二元一次方程组的解互为相反数,求k的值.
四、解答题(本大题3小题,每小题8分,共24分)
21.(8分)如图,已知AB∥CD,点B、C、F在同一条直线上,BD平分∠ABC,CE平分∠DCF,AC⊥CE,AC与BD相交于点P,求证:AC⊥BD.
22.(8分)为积极响应垃圾分类活动,某学校开展了主题为“打造无废校园,助力无废城市”的宣传活动.为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调査,将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如图不完整的统计表和条形统计图.
等级
频数
频率
优秀
19
38%
良好
m
44%
合格
7
n%
不合格
2
4%
(1)本次调查随机抽取了 名学生;表中m= ,n= ;
(2)补全条形统计图;
(3)垃圾分类节约资源,还地球一个碧海蓝天,写一句关于垃圾分类的宣传标语,要求20字以内;
(4)若全校有1500名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人?
23.(8分)某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共12辆.若购买A型公交车1辆、B型公交车2辆,共需440万元;若购买A型公交车2辆、B型公交车1辆,共需400万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为64万人次和120万人次.若该公司购买A型和B型公交车的总费用不超过1660万元,且确保这12辆公交车在该线路的年均载客量总和不少于910万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
2019-2020学年安徽省铜陵市七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本大题10小题,共30分)
1.(3分)下列语句是命题的是( )
A.你有橡皮擦吗 B.小华是男生
C.垃圾要分类 D.出门戴口罩
【分析】根据命题的定义分别进行判断.
【解答】解:垃圾要分类和出门戴口罩都是描叙性语言,它们都不是命题;“你有橡皮擦吗?”是疑问句,它不是命题;小华是男生是命题.
故选:B.
2.(3分)的算术平方根是( )
A.4 B.±4 C.2 D.±2
【分析】先计算的值,再根据算术平方根的定义求解.
【解答】解:=4,
4的算术平方根2,
故选:C.
3.(3分)已知点P(m+2,2m﹣4)在x轴上,则点P的坐标是( )
A.(4,0) B.(0,4) C.(﹣4,0) D.(0,﹣4)
【分析】直接利用关于x轴上点的坐标特点得出m的值,进而得出答案.
【解答】解:∵点P(m+2,2m﹣4)在x轴上,
∴2m﹣4=0,
解得:m=2,
∴m+2=4,
则点P的坐标是:(4,0).
故选:A.
4.(3分)2020年5月20日,随着第一批考生经体温检测等流程后进入考点,铜陵市2020年初中学业水平体育考试正式拉开序幕.据了解,铜陵市共有1.7万名考生报名参加体育考试,为了了解考生体育成绩,从中抽取2000名考生的体育成绩进行统计,在这个问题中样本是( )
A.1.7万名考生 B.2000名考生
C.1.7万名考生体育成绩 D.2000名考生的体育成绩
【分析】总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
【解答】解:在这个问题中样本是2000名考生的体育成绩.
故选:D.
5.(3分)如图,直线a∥b,∠1=50°,∠2=30°,则∠3的度数为( )
A.40° B.90° C.50° D.100°
【分析】由平行线的性质得∠1=∠4=50°,根据平角的定义和角的和差求得∠3的度数为100°.
【解答】解:如图所示:
∵a∥b,
∴∠1=∠4,
又∵∠1=50°,
∴∠4=50°,
又∵∠2+∠3+∠4=180°,∠2=30°,
∴∠3=100°,
故选:D.
6.(3分)若8xmy与6x3yn的和是单项式,则(m+n)3的平方根为( )
A.4 B.8 C.±4 D.±8
【分析】根据单项式的和是单项式,可得同类项,根据同类项是字母项相同且相同字母的指数也相同,可得m、n的值,再代入计算可得答案.
【解答】解:由8xmy与6x3yn的和是单项式,得
m=3,n=1.
(m+n)3=(3+1)3=64,64的平方根为±8.
故选:D.
7.(3分)如图,快艇从P处向正北航行到A处时,向左转50°航行到B处,再向右转80°继续航行,此时的航行方向为( )
A.北偏东30° B.北偏东80° C.北偏西30° D.北偏西50°
【分析】根据平行线的性质,可得∠2,根据角的和差,可得答案.
【解答】解:如图,
AP∥BC,
∴∠2=∠1=50°.
∠3=∠4﹣∠2=80°﹣50°=30°,
此时的航行方向为北偏东30°,
故选:A.
8.(3分)下列说法正确的是( )
A.直线外一点到这条直线的垂线叫做点到直线的距离
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.同旁内角互补是真命题
D.经过一点,有且只有一条直线与这条直线平行
【分析】利用点到直线的距离的定义、平行线的性质及平行公理对每个选项进行判断后即可确定正确的选项.
【解答】解:A、直线外一点到这条直线的垂线段的长度叫做点到直线的距离,故原命题错误,不符合题意;
B、符合垂直的性质,正确,符合题意;
C、两直线平行,同旁内角互补,故原命题错误,不符合题意;
D、经过直线外一点,有且只有一条直线与这条直线平行,故原命题错误,不符合题意;
故选:B.
9.(3分)已知x=2是不等式(x﹣5)(ax﹣3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是( )
A.a>1 B.a≤2 C.1<a≤2 D.1≤a≤2
【分析】根据x=2是不等式(x﹣5)(ax﹣3a+2)≤0的解,且x=1不是这个不等式的解,列出不等式,求出解集,即可解答.
【解答】解:∵x=2是不等式(x﹣5)(ax﹣3a+2)≤0的解,
∴(2﹣5)(2a﹣3a+2)≤0,
解得:a≤2,
∵x=1不是这个不等式的解,
∴(1﹣5)(a﹣3a+2)>0,
解得:a>1,
∴1<a≤2,
故选:C.
10.(3分)小慧去花店购买鲜花,若买5支玫瑰和3支百合,则她所带的钱还剩下10元;若买3支玫瑰和5支百合,则她所带的钱还缺4元.若只买8支玫瑰,则她所带的钱还剩下( )
A.31元 B.30元 C.25元 D.19元
【分析】设每支玫瑰x元,每支百合y元,根据总价=单价×数量结合小慧带的钱数不变,可得出关于x,y的二元一次方程,整理后可得出y=x+7,再将其代入5x+3y+10﹣8x中即可求出结论.
【解答】解:设每支玫瑰x元,每支百合y元,
依题意,得:5x+3y+10=3x+5y﹣4,
∴y=x+7,
∴5x+3y+10﹣8x=5x+3(x+7)+10﹣8x=31.
故选:A.
二、填空题(本大题6小题,每小题3分,共18分)
11.(3分)不等式2x+3>3x的解集为 x<3 .
【分析】移项、合并同类项,系数化为1即可求出不等式的解集.
【解答】解:2x+3>3x,
移项得:2x﹣3x>﹣3,
合并得:﹣x>﹣3,
系数化为1得:x<3.
故答案为x<3.
12.(3分)在第二象限,到x轴距离为4,到y轴距离为3的点P的坐标是 (﹣3,4) .
【分析】应先判断出点P的横、纵坐标的符号,进而根据到坐标轴的距离判断点P的具体坐标.
【解答】解:∵P在第二象限,
∴点P的横坐标小于0,纵坐标大于0;
又∵点P到x轴的距离是4,即点P的纵坐标为4;点P到y轴的距离为3,即点P的横坐标为﹣3,
∴点P的坐标是(﹣3,4);
故答案是:(﹣3,4).
13.(3分)在平面直角坐标系中,三角形ABC的三个顶点的坐标分别是A(2,3),B(0,4),C(0,﹣2),则三角形ABC的面积为 2 .
【分析】直接利用三角形的面积公式解答.
【解答】解:如图,BC=4+2=6.
所以S△ABC=BC•xA==6.
故答案是:2.
14.(3分)把一根9m长的钢管截成1m长和2m长两种规格均有的短钢管,且没有余料,设某种截法中1m长的钢管有a根,则a的值可能有 4 种.
【分析】设某种截法中1m长的钢管有a根,2m长的钢管有b根,根据两种规格钢管的总长度为9m,即可得出关于a,b的二元一次方程,结合a,b均为正整数,即可找出各种截法,进而可得出结论.
【解答】解:设某种截法中1m长的钢管有a根,2m长的钢管有b根,
依题意,得:a+2b=9,
∴a=9﹣2b.
∵a,b均为正整数,
∴当b=1时,a=7;当b=2时,a=5;当b=3时,a=3;当b=4时,a=1,
∴a的值可能有4种.
故答案为:4.
15.(3分)如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(﹣1,0),(0,),现将该三角板向右平移使点A与点O重合,得到△OCB',再△OCB′绕O点顺时针旋转90°得到△OC′B″将则点B的对应点B″的坐标是 (,﹣1) .
【分析】如图,由题意B′(1,).
【解答】解:如图,由题意B′(1,).
∵△OCB′≌△OC′B″,
∴OC=OC′=1,C′B″=CB′=,
∴B″(,﹣1).
故答案为(,﹣1).
16.(3分)小华在文具超市挑选了6支中性笔和5本笔记本.结账时,小华付款50元,营业店员找零4元,小华说:“阿姨您好,6支中性笔和5本笔记本一共42元,应该找零8元.”店员说:“啊…哦,我明白了,小朋友你真棒,我刚才把中性笔和笔记本的单价弄反了,对不起,再找给你4元”.根据两人的对话计算:若购买一支中性笔和一本笔记本一共需要付款 8 元.
【分析】设购买一支中性笔x元,购买一本笔记本y元,根据“6支中性笔和5本笔记本一共42元”、“5支中性笔和6本笔记本一共46元”列出方程组并解答.
【解答】解:设购买一支中性笔x元,购买一本笔记本y元,则.
由①+②,得11(x+y)=88.
所以x+y=8.
即:购买一支中性笔和一本笔记本一共需要付款8元.
故答案是:8.
三、计算题(本大题4小题,每小题7分,共28分)
17.(7分)计算:(﹣1)2020﹣(+)+.
【分析】原式利用乘方的意义,平方根、立方根性质计算即可求出值.
【解答】解:原式=1﹣(6+)+3
=1﹣7+3
=﹣3.
18.(7分)解方程组:.
【分析】方程组利用加减消元法求出解即可.
【解答】解:,
①﹣②×4得:11y=﹣11,即y=﹣1,
把y=﹣1代入②得:x=2,
则方程组的解为.
19.(7分)解不等式组:,并将解集在数轴上表示出来.
【分析】先求出每个不等式的解集,再求出不等式组的解集,最后在数轴上表示出来即可.
【解答】解:,
解不等式①得:x>﹣1,
解不等式②得:x≤1,
∴不等式组的解集为﹣1<x≤1,
在数轴上表示为:
.
20.(7分)已知关于x,y的二元一次方程组的解互为相反数,求k的值.
【分析】用含k的代数式表示x和y,根据方程组的解互为相反数可得x+y=0,列出关于k的方程,进而可得k的值.
【解答】解:∵方程组的解互为相反数,
∴x+y=0,
∴
∴②﹣①得,2x=﹣2,
∴x=﹣1,
∴y=1,
把x=﹣1,y=1代入2x﹣y=k中,
∴2×(﹣1)﹣1=k,
∴k=﹣3.
答:k的值为﹣3.
四、解答题(本大题3小题,每小题8分,共24分)
21.(8分)如图,已知AB∥CD,点B、C、F在同一条直线上,BD平分∠ABC,CE平分∠DCF,AC⊥CE,AC与BD相交于点P,求证:AC⊥BD.
【分析】根据平行线的性质可以得到∠1、∠2、∠3、∠4之间的关系,再根据AC⊥CE,即可得到∠4+∠PCB=90°,然后即可得到∠2+∠PCB=90°,从而可以得到结论成立.
【解答】证明:∵AB∥CD,
∴∠ABC=∠DCF,
∵BD平分∠ABC,CE平分∠DCF,
∴∠1=∠2=∠3=∠4,
∵AC⊥CE,
∴∠4+∠PCB=90°,
∴∠2+∠PCB=90°,
∴∠BPC=90°,
∴AC⊥BD.
22.(8分)为积极响应垃圾分类活动,某学校开展了主题为“打造无废校园,助力无废城市”的宣传活动.为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调査,将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如图不完整的统计表和条形统计图.
等级
频数
频率
优秀
19
38%
良好
m
44%
合格
7
n%
不合格
2
4%
(1)本次调查随机抽取了 50 名学生;表中m= 22 ,n= 14 ;
(2)补全条形统计图;
(3)垃圾分类节约资源,还地球一个碧海蓝天,写一句关于垃圾分类的宣传标语,要求20字以内;
(4)若全校有1500名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人?
【分析】(1)用优秀的人数除以优秀的人数所占的百分比即可得到抽查的人数,然后即可计算出m、n的值;
(2)根据(1)中m的值,可以将条形统计图补充完整;
(3)本题答案不唯一,只要合理即可;
(4)根据频数分布表中的数据,即可计算出该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
【解答】解:(1)本次调查随机抽取了19÷38%=50名学生,
m=50×44%=22,n%=×100%=14%,
故答案为:50,22,14;
(2)由(1)知,m=22,
补全的条形统计图如右图所示;
(3)如果你能做好垃圾分类,那么地球就会给你一个碧海蓝天;
(4)1500×(38%+44%)=1230(人),
答:该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有1230人.
23.(8分)某公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共12辆.若购买A型公交车1辆、B型公交车2辆,共需440万元;若购买A型公交车2辆、B型公交车1辆,共需400万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为64万人次和120万人次.若该公司购买A型和B型公交车的总费用不超过1660万元,且确保这12辆公交车在该线路的年均载客量总和不少于910万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
【分析】(1)设购买A型公交车每辆需要x万元,购买B型公交车每辆需要y万元,根据“若购买A型公交车1辆、B型公交车2辆,共需440万元;若购买A型公交车2辆、B型公交车1辆,共需400万元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买m辆A型公交车,则购买(12﹣m)辆B型公交车,根据“购买A型和B型公交车的总费用不超过1660万元,且确保这12辆公交车在该线路的年均载客量总和不少于910万人次”,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,再结合m为正整数即可得出各购车方案,设购车总费用为w万元,利用总价=单价×数量,即可得出w关于m的函数关系式,利用一次函数的性质即可解决最值问题.
【解答】解:(1)设购买A型公交车每辆需要x万元,购买B型公交车每辆需要y万元,
依题意,得:,
解得:.
答:购买A型公交车每辆需要120万元,购买B型公交车每辆需要160万元.
(2)设购买m辆A型公交车,则购买(12﹣m)辆B型公交车,
依题意,得:,
解得:6≤m≤9.
又∵m为正整数,
∴m可以为7,8,9,
∴该公司有3种购车方案,方案1:购买7辆A型公交车,5辆B型公交车;方案2:购买8辆A型公交车,4辆B型公交车;方案3:购买9辆A型公交车,3辆B型公交车.
设购车总费用为w万元,则w=120m+160(12﹣m)=﹣40m+1920,
∵k=﹣40<0,
∴w随m的增大而减小,
∴当m=9时,w取得最小值,最小值=﹣40×9+1920=1560,
∴方案3购买9辆A型公交车,3辆B型公交车总费用最少,最少总费用为1560万元.
相关资料
更多








