初中数学北师大版九年级上册3 正方形的性质与判定精品练习题

这是一份初中数学北师大版九年级上册3 正方形的性质与判定精品练习题，共15页。试卷主要包含了3 正方形的性质与判定，5°C．22，5°，等内容，欢迎下载使用。
1.3 正方形的性质与判定


一．选择题


1．矩形、菱形、正方形都具有的性质是（ ）


A．对角线互相垂直


B．对角线相等


C．对角线互相平分


D．每一条对角线平分一组对角


2．正方形具有而矩形不具有的性质是（ ）


A．对角相等B．对角线互相平分


C．对角线相等D．对角线互相垂直


3．如图，正方形ABCD中，AB＝1，则AC的长是（ ）





A．1B．C．D．2


4．正方形ABCD中，对角线AC、BD交于点O，则∠CBO等于（ ）


A．30°B．45°C．60°D．75°


5．如图，已知E是正方形ABCD对角线AC上一点，且AB＝AE，则∠DBE度数是（ ）





A．15°B．32.5°C．22.5°D．30°


6．如图，以正方形ABCD的中心为原点建立平面直角坐标系，点A的坐标为（2，2），则点D的坐标为（ ）





A．（2，2）B．（﹣2，2）C．（﹣2，﹣2）D．（2，﹣2）


7．如图，正方形ABCD中，点E在BC上，且CE＝BC，点F是CD的中点，延长AF与BC的延长线交于点M．以下结论：


①AB＝CM；②AE＝AB+CE；③S△AEF＝S四边形ABCF；④∠AFE＝90°．


其中正确结论的个数有（ ）





A．1个B．2个C．3个D．4个


8．如图，四边形ABCD为正方形，A点坐标为（﹣1，0），点B，C，D分别在坐标轴上，则正方形的周长是（ ）





A．4B．3C．4D．2


二．填空题


9．正方形的边长为，则这个正方形的对角线长为 ．


10．如图，四边形ABCD是矩形，则只须补充条件 （用字母表示只添加一个条件）就可以判定四边形ABCD是正方形．





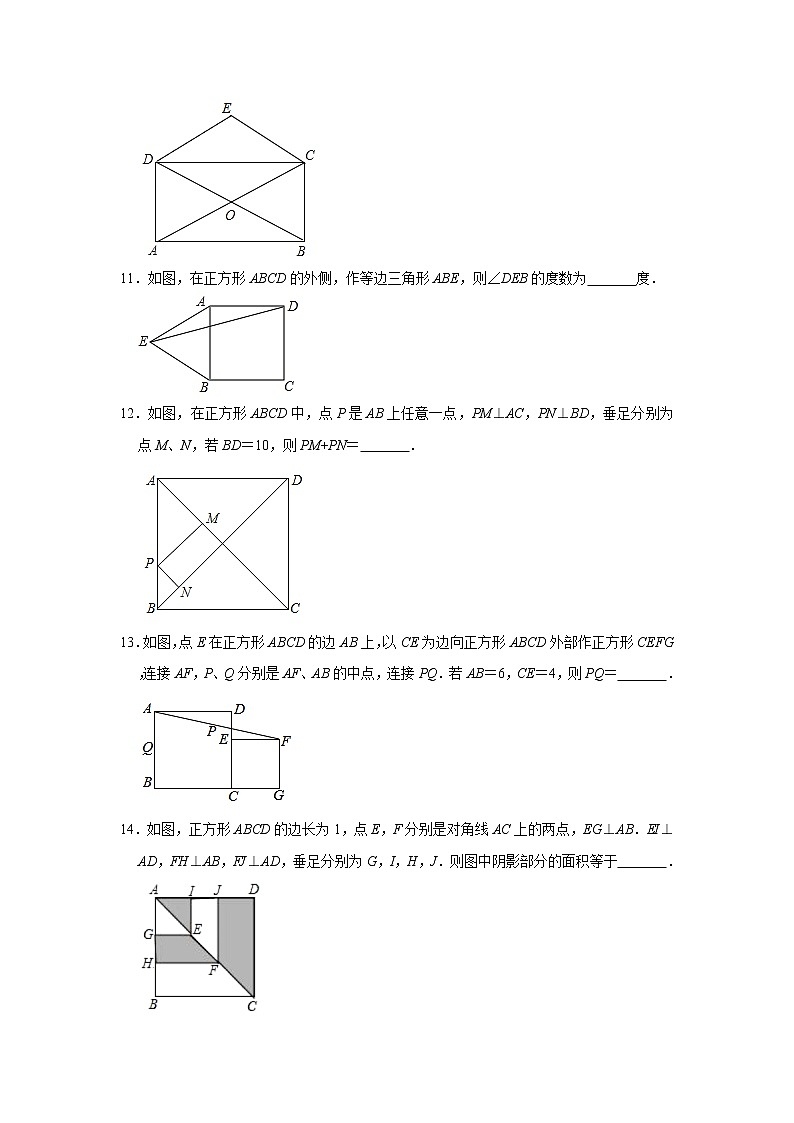
11．如图，在正方形ABCD的外侧，作等边三角形ABE，则∠DEB的度数为 度．





12．如图，在正方形ABCD中，点P是AB上任意一点，PM⊥AC，PN⊥BD，垂足分别为点M、N，若BD＝10，则PM+PN＝ ．





13．如图，点E在正方形ABCD的边AB上，以CE为边向正方形ABCD外部作正方形CEFG，连接AF，P、Q分别是AF、AB的中点，连接PQ．若AB＝6，CE＝4，则PQ＝ ．





14．如图，正方形ABCD的边长为1，点E，F分别是对角线AC上的两点，EG⊥AB．EI⊥AD，FH⊥AB，FJ⊥AD，垂足分别为G，I，H，J．则图中阴影部分的面积等于 ．





15．如图，在正方形ABCD中，点P在AB边上，AE⊥DP于E点，CF⊥DP于F点，若AE＝4，CF＝7，则EF＝ ．





16．如图，正方形ABCD的边长为6，点E，F分别在边AB，BC上，若F是BC的中点，且∠EDF＝45°，则BE的长为





三．解答题（共5小题）


17．如图，等边△AEF的顶点E，F在矩形ABCD的边BC，CD上，且∠CEF＝45°．求证：矩形ABCD是正方形．





18．如图，在正方形ABCD中，点E在BC边的延长线上，点F在CD边的延长线上，且CE＝DF，连接AE和BF相交于点M．


求证：AE＝BF．





19．如图，四边形ABCD是正方形，E是CD边上任意一点，连接AE，作BF⊥AE，DG⊥AE，垂足分别为F、G．


求证：AF＝DG





20．在正方形ABCD中，M、N分别是边CD、AD的中点，连接BN，AM交于点E．求证：AM⊥BN．





21．如图，正方形ABCD中，E是CD边的中点，F是BC边上一点，∠FAE＝∠DAE．


（1）求证：AF＝AD+CF；


（2）已知正方形ABCD的边长为4．


①求AF之长；


②若P是AE上一点，且△DEP是等腰三角形，则线段EP的长为 ．




















参考答案


一．选择题


1．解：因为矩形的对角线互相平分且相等，


菱形的对角线互相平分且垂直且平分每一组对角，


正方形的对角线具有矩形和菱形所有的性质，


所有矩形、菱形和正方形的对角线都具有的性质是对角线互相平分，


故选：C．


2．解：因为正方形的对角相等，对角线相等、垂直、且互相平分，矩形的对角相等，对角线相等，互相平分，


所以正方形具有而矩形不具有的性质是对角线互相垂直．


故选：D．


3．解：在Rt△ABC中，AB＝BC＝1，


∴AC＝＝＝；


故选：B．


4．解：正方形的对角线即角平分线，AC、BD交于点O，


则∠CBO＝＝45°，


故选：B．


5．解：∵AC、BD是正方形ABCD对角线，


∴∠BAE＝∠ABD＝45°，


又AB＝AE，


∴∠ABE＝∠AEB＝67.5°，


∴∠DBE＝67.5°﹣45°＝22.5°，


故选：C．


6．解：如图所示：∵以正方形ABCD的中心O为原点建立坐标系，点A的坐标为（2，2），


∴点B、C、D的坐标分别为：（2，﹣2），（﹣2，﹣2），（﹣2，2）．


故选：B．


7．解：由题意知，


∵点F是CD的中点，


∴DF＝CF，


在△ADF和△MCF中，


，


∴△ADF≌△MCF（ASA），


∴CM＝AD＝AB，


①正确；


设正方形ABCD边长为4，


∵CE＝BC＝1，


∴BE＝3，


∴AE＝5，


∴AE＝AB+CE，


②正确；


EM＝CM+CE＝5＝AE，


又∵F为AM的中点，


∴EF⊥AM，


④正确，


由CF＝2，CE＝1得EF＝，


由DF＝2，AD＝4得AF＝2，


∴S△AEF＝5，


又∵S△ADF＝4，


∴S四边形ABCF＝S□ABCD﹣S△ADF＝12，


∴S△AEF＝S四边形ABCF≠S四边形ABCF；


③不正确，


∴正确的有3个，


故选：C．


8．解：在正方形ABCD中，


∠DAO＝45°，


∵A（﹣1，0），


∴OA＝1，


∴AD＝，


∵AD＝CD＝BC＝AB，


∴正方形的周长为4，


故选：C．


二．填空题


9．解：如图，连接AC，





∵四边形ABCD是正方形，


∴AB＝BC＝，∠B＝90°，


∴AC＝AB＝2，


故答案为：2．


10．解：因为有一组邻边相等的矩形是正方形，


故答案为：AB＝AD（答案不唯一）．


11．解：∵四边形ABCD是正方形


∴AB＝AD，∠BAD＝90°


∵△ABE是等边三角形


∴AE＝AB，∠BAE＝∠BEA＝60°


∴AD＝AE，∠DAE＝150°


∴∠AED＝∠ADE＝（180°﹣∠DAE）＝15°


∴∠DEB＝∠BEA﹣∠AED＝60°﹣15°＝45°


故答案为：45．


12．解：在正方形ABCD中，


∴AC⊥BD，∠ABO＝45°，


∵PM⊥AC，PN⊥BD，


∴四边形PMON是矩形，


∴PM＝ON，


∵PN＝BN，


∴PM+PN＝ON+BN＝OB＝BD＝5，


故答案为：5





13．解：连接BF，





∵正方形ABCD和正方形CEFG中，AB＝6，CE＝4，


∴GF＝GC＝4，BC＝6，


∴BG＝GC+BC＝4+6＝10，


∴BF＝，


∵P、Q分别是AF、AB的中点，


∴PQ＝BF＝．


故答案．


14．解：∵在正方形ABCD中，点E，F分别是对角线AC上的两点，EG⊥AB．EI⊥AD，FH⊥AB，FJ⊥AD，


∴四边形EGHF和四边形EIJF是两个全等的四边形，它们的面积相等，


∴阴影部分的面积等于△ACD的面积，


∵正方形ABCD的边长为1，


∴AD＝CD＝1，∠D＝90°，


∴△ACD的面积是：＝，


故答案为：．


15．解：∵四边形ABCD是正方形


∴AD＝DC，∠ADC＝90°


∵AE⊥DP，CF⊥DP


∴∠AED＝∠DFC＝90°


∵∠ADE+∠CDF＝∠CDF+∠DCF＝90°


∴∠ADE＝∠DCF


在△ADE和△DCF中





∴△ADE≌△DCF（AAS）


∴AE＝DF＝4，DE＝CF＝7


∴EF＝DE﹣DF＝7﹣4＝3


故答案为：3．


16．解：延长F至G，使CG＝AE，连接DG、EF，如图所示：


∵四边形ABCD是正方形，


∴AD＝AB＝BC＝CD＝6，∠A＝∠B＝∠DCF＝∠ADC＝90°，


∴∠DCG＝90°，


在△ADE和△CDG中，，


∴△ADE≌△CDG（SAS），


∴DE＝DG，∠ADE＝∠CDG，


∴∠EDG＝∠CDE+∠CDG＝∠CDE+∠ADE＝90°，


∵∠EDF＝45°，


∴∠GDF＝45°，


在△EDF和△GDF中，，


∴△EDF≌△GDF（SAS），


∴EF＝GF，


∵F是BC的中点，


∴BF＝CF＝3，


设AE＝CG＝x，则EF＝GF＝x＝3+x，


在Rt△BEF中，由勾股定理得：32+（6﹣x）2＝（3+x）2，


解得：x＝2，即AE＝2，


∴BE＝AB﹣AE＝6﹣2＝4，


故答案为：4．





三．解答题


17．解：∵四边形ABCD是矩形，


∴∠B＝∠D＝∠C＝90°，


∵△AEF是等边三角形，


∴AE＝AF，∠AEF＝∠AFE＝60°，


∵∠CEF＝45°，


∴∠CFE＝∠CEF＝45°，


∴∠AFD＝∠AEB＝180°﹣45°﹣60°＝75°，


∴△AEB≌△AFD（AAS），


∴AB＝AD，


∴矩形ABCD是正方形．


18．解：在正方形ABCD中，


AB＝CD＝CD＝AD，


∵CE＝DF，


∴BE＝CF，


在△AEB与△BFC中，


，


∴△AEB≌△BFC（SAS），


∴AE＝BF．


19．解：∵四边形ABCD是正方形，


∴AB＝AD，∠DAB＝90°，


∵BF⊥AE，DG⊥AE，


∴∠AFB＝∠AGD＝∠ADG+∠DAG＝90°，


∵∠DAG+∠BAF＝90°，


∴∠ADG＝∠BAF，


在△BAF和△ADG中，


∵，


∴△BAF≌△ADG（AAS），


∴AF＝DG，


20．证明：∵四边形ABCD是正方形，


∴AB＝BC＝CD＝DA，∠BAN＝∠ADM＝90°，


∵M、N分别是边CD、AD的中点，


∴AN＝AD，DM＝CD，


∴AN＝DM，


在△ABN和△DAM中，，


∴△ABN≌△DAM（SAS），


∴∠ABN＝∠DAM，


∵∠DAM+∠BAE＝90°，


∴∠ABN+∠BAE＝90°，


∴∠AEB＝90°，


∴AM⊥BN．


21．（1）证明：如图1，过E点作EG⊥AF，垂足为G，连接EF，





（也可延长AE、BC交于P，用全等和等腰三角形知识解决），


∵EG⊥AF，


∴∠EGF＝∠AGE＝90°，


∵四边形ABCD是正方形，


∴∠C＝∠D＝90°，


在△AGE和△ADE中，





∴△AGE≌△ADE（AAS），


∴AD＝AG，GE＝DE，


∵E是CD边的中点，


∴CE＝DE，


∴GE＝CE，


在Rt△EGF和Rt△ECF中，





∴Rt△EGF≌Rt△ECF（HL），


∴GF＝CF，


∵AF＝AG+GF，


∴AF＝AD+CF；


（2）解：①设CF＝x，则BF＝4﹣x，AF＝4+x，


在Rt△ABF中，AB2+BF2＝AF2，


∴42+（4﹣x）2＝（4+x）2，


解得：x＝1，


∴AF＝4+x＝4+1＝5；


②分三种情况：


i）如图2，PD＝DE，过D作DG⊥AE于G，





∴EP＝2EG，


Rt△ADE中，AD＝4，DE＝2，


∴AE＝＝2，


∴S△ADE＝，


即，


∴DG＝＝，


由勾股定理得：EG＝＝＝，


∴EP＝2EG＝；


ii）如图3，EP＝DE＝2；





iii）如图4，PD＝PE，过P作PM⊥DE于M，则DM＝EM，





∵AD⊥CD，PM⊥DE，


∴AD∥PM，


∴AP＝PE，


∵AE＝2，


∴EP＝，


综上，EP的长是2或或．