数学必修 第一册第一章 集合与常用逻辑用语本章综合与测试优质学案设计

这是一份数学必修 第一册第一章 集合与常用逻辑用语本章综合与测试优质学案设计，共5页。学案主要包含了集合的综合运算，充分条件，全称量词命题与存在量词命题等内容，欢迎下载使用。













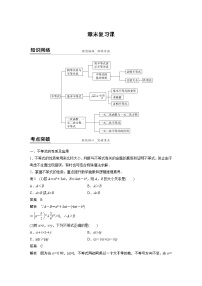
一、集合的综合运算


1．集合的运算有交、并、补这三种常见的运算，它是集合中的核心内容．在进行集合的运算时，往往由于运算能力差或考虑不全面而极易出错，此时，数轴分析(或Venn图)是个好帮手，能将复杂问题直观化．在具体应用时要注意检验端点值是否适合题意，以免增解或漏解．


2．掌握集合的基本关系与基本运算，重点提升逻辑推理和数学运算素养．


例1 已知集合A＝{x|0≤x≤2}，B＝{x|a≤x≤a＋3}．


(1)若(∁RA)∪B＝R，求a的取值范围；


(2)是否存在a使(∁RA)∪B＝R且A∩B＝∅？


解 (1)∵A＝{x|0≤x≤2}，


∴∁RA＝{x|x<0或x>2}．


∵(∁RA)∪B＝R，





∴eq \b\lc\{\rc\ (\a\vs4\al\c1(a≤0，,a＋3≥2，))∴－1≤a≤0.


所以a的取值范围为{a|－1≤a≤0}．


(2)由(1)知(∁RA)∪B＝R时，


－1≤a≤0，而2≤a＋3≤3，


∴A⊆B，这与A∩B＝∅矛盾．


即这样的a不存在．


反思感悟 借助数轴表达集合间的关系可以更直观，但操作时要规范，如区间端点的顺序、虚实不能标反．


跟踪训练1 已知全集U＝{x|x≤4}，集合A＝{x|－2

解 把集合U及集合A，B分别在数轴上表示出来．


如图，





∁UA＝{x|x≤－2或3≤x≤4}，A∩B＝{x|－2

∁U(A∩B)＝{x|x≤－2或3≤x≤4}，


(∁UA)∩B＝{x|－3

二、充分条件、必要条件与充要条件


1．若p⇒q，且q⇏p，则p是q的充分不必要条件，同时q是p的必要不充分条件；


若p⇔q，则p是q的充要条件，同时q是p的充要条件．


2．掌握充要条件的判断和证明，提升逻辑推理和数学运算素养．


例2 设p：实数x满足A＝{x|x≤3a，或x≥a(a<0)}．


q：实数x满足B＝{x|－4≤x<－2}．


且q是p的充分不必要条件，求实数a的取值范围．


解 ∵q是p的充分不必要条件．


∴BA，


∴eq \b\lc\{\rc\ (\a\vs4\al\c1(a≤－4，,a<0))或eq \b\lc\{\rc\ (\a\vs4\al\c1(3a≥－2，,a<0，))


解得－eq \f(2,3)≤a<0或a≤－4.


所以a的范围为eq \b\lc\{\rc\}(\a\vs4\al\c1(a\b\lc\|\rc\ (\a\vs4\al\c1(－\f(2,3)≤a<0，或a≤－4)))).


反思感悟 在判定充分条件、必要条件时，要注意既要看由p能否推出q，又要看由q能否推出p，不能顾此失彼．


跟踪训练2 (1)已知集合A＝{x|－4≤x≤4，x∈R}，B＝{x|x5”是“A⊆B”的( )


A．充分不必要条件


B．必要不充分条件


C．充要条件


D．既不充分又不必要条件


答案 A


解析 A⊆B⇔a>4，而a>5⇒a>4，且a>4⇏a>5，所以“a>5”是“A⊆B”的充分不必要条件．


(2)“不等式x2－2x＋m≥0在R上恒成立”的一个充分不必要条件是( )


A．m≥1 B．m≤1 C．m≥0 D．m≥2


答案 D


解析 “不等式x2－2x＋m≥0在R上恒成立”的充要条件为：“(－2)2－4m≤0”即“m≥1”，


又“m≥2”是“m≥1”的充分不必要条件，


即“不等式x2－2x＋m≥0在R上恒成立”的一个充分不必要条件是“m≥2”，


故选D.


三、全称量词命题与存在量词命题


1．全称量词命题的否定一定是存在量词命题，存在量词命题的否定一定是全称量词命题．首先改变量词，把全称量词改为存在量词，把存在量词改为全称量词，然后把判断词加以否定．


2．通过含有量词的命题的否定及利用命题的真假求参数范围等，培养逻辑推理和数学运算素养．


例3 (1) 命题“∀x∈R，x2－2x＋1≥0”的否定是( )


A．∃x∈R，x2－2x＋1≤0


B．∃x∈R，x2－2x＋1≥0


C．∃x∈R，x2－2x＋1<0


D．∀x∈R，x2－2x＋1<0


答案 C


解析 ∵命题“∀x∈R，x2－2x＋1≥0”为全称量词命题，


∴命题的否定为：∃x∈R，x2－2x＋1<0，


故选C.


(2)若命题p：∀x∈R，x2－2x＋m≠0是真命题，则实数m的取值范围是( )


A．m≥1 B．m>1 C．m<1 D．m≤1


答案 B


解析 命题p：∀x∈R，x2－2x＋m≠0是真命题，则m≠－(x2－2x)，


∵－(x2－2x)＝－(x－1)2＋1≤1，


∴m>1.


∴实数m的取值范围是{m|m>1}．


故选B.


反思感悟 全称量词命题、存在量词命题真假判断


(1)全称量词命题的真假判定：要判定一个全称量词命题为真，必须对限定集合M中每一个x验证p(x)成立，一般用代数推理的方法加以证明；要判定一个全称量词命题为假，只需举出一个反例即可．


(2)存在量词命题的真假判定：要判定一个存在量词命题为真，只要在限定集合M中，找到一个x，使p(x)成立即可；否则，这一存在量词命题为假．


跟踪训练3 (1)∃m，n∈Z，使得m2＝n2＋2 019的否定是( )


A．∀m，n∈Z，使得m2＝n2＋2 019


B．∃m，n∈Z，使得m2≠n2＋2 019


C．∀m，n∈Z，使得m2≠n2＋2 019


D．以上都不对


答案 C


(2)设命题p：∀x∈R，x2＋ax＋2<0，若綈p为真，则实数a的取值范围是________．


答案 R


解析 綈p：∃x∈R，x2＋ax＋2≥0为真命题，


显然a∈R.





1．设全集U＝R，集合A＝{x|－3

A．{x|x≤－3或x≥1} B．{x|x<－1或x≥3}


C．{x|x≤3} D．{x|x≤－3}


答案 D


解析 A＝{x|－3－3}，∁U(A∪B)＝{x|x≤－3}，故选D.


2．下列命题中是全称量词命题并且是真命题的是( )


A．∀x∈R，x2＋2x＋1>0


B．∃x∈N,2x为偶数


C．所有菱形的四条边都相等


D．π是无理数


答案 C


解析 对A，是全称量词命题，但不是真命题；故A不正确；对B，是真命题，但不是全称量词命题，故B不正确；对C，是全称量词命题，也是真命题，故C正确；对D，是真命题，但不是全称量词命题，故D不正确，故选C.


3．设集合A＝{x|1

A．{a|a≥2} B．{a|a≤1}


C．{a|a≥1} D．{a|a≤2}


答案 A


解析 如图





4．已知集合A＝{1,3,2－m}，集合B＝{3，m2}，则“B⊆A”的充要条件是实数m＝________.


答案 －2


解析 若B⊆A，


则m2＝1或m2＝2－m，


得m＝1或m＝－1，或m＝－2，


当m＝1时，A＝{1,3,1}不成立，


当m＝－1时，A＝{1,3,3}不成立，


当m＝－2时，A＝{1,3,4}，B＝{3,4}，满足条件．


即m＝－2，


则“B⊆A”的充要条件是实数m＝－2.


5．已知集合A＝{2,0,1,9}，B＝{k|k∈R，k2－2∈A，k－2∉A}，则集合B中所有的元素之和为________．


答案 －2


解析 若k2－2＝2，则k＝2或k＝－2，当k＝2时，k－2＝0，不满足条件，当k＝－2时，k－2＝－4，满足条件；若k2－2＝0，则k＝±eq \r(2)，显然满足条件；若k2－2＝1，则k＝±eq \r(3)，显然满足条件；若k2－2＝9，得k＝±eq \r(11)，显然满足条件．所以集合B中的元素为－2，±eq \r(2)，±eq \r(3)，±eq \r(11)，所以集合B中的所有元素之和为－2.