

还剩15页未读,
继续阅读
2019-2020学年湖南省邵阳市邵东县七年级(下)期末数学试卷 解析版
展开
2019-2020学年湖南省邵阳市邵东县七年级(下)期末数学试卷
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)请将正确答案的代号填写在答题卡上.
1.(3分)如下字体的四个汉字中,可以看作是轴对称图形的是( )
A.中 B.国 C.加 D.油
2.(3分)如图,已知∠1=65°,如果CD∥BE,那么∠B的度数为( )
A.65° B.105° C.115° D.125°
3.(3分)下列运算正确的是( )
A.a2+a3=2a5 B.(a﹣b)2=a2﹣b2
C.a3•a5=a15 D.(ab2)2=a2b4
4.(3分)下列各式中,不能够用平方差公式计算的是( )
A.( y+2x)(2x﹣y) B.(﹣x﹣3y)(x+3y)
C.(2x2﹣y2 )(2x2+y2 ) D.(4a+b﹣c)(4a﹣b﹣c)
5.(3分)若a﹣b=1,a2+b2=13,则ab等于( )
A.6 B.7 C.﹣6 D.﹣7
6.(3分)《九章算术》中记载:“今有人共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”意思是:现在一些人共同买一个物品,每人出8元,还余3元;每人出7元,还差4元.问共有多少人?这个物品价格是多少元?设共有x个人,这个物品价格是y元.则可列方程组为( )
A. B.
C. D.
7.(3分)下列各式从左到右因式分解正确的是( )
A.2x﹣6y+2=2(x﹣3y) B.x2﹣2x+1=x(x﹣2)+1
C.x2﹣4=(x﹣2)2 D.x3﹣x=x(x+1)(x﹣1)
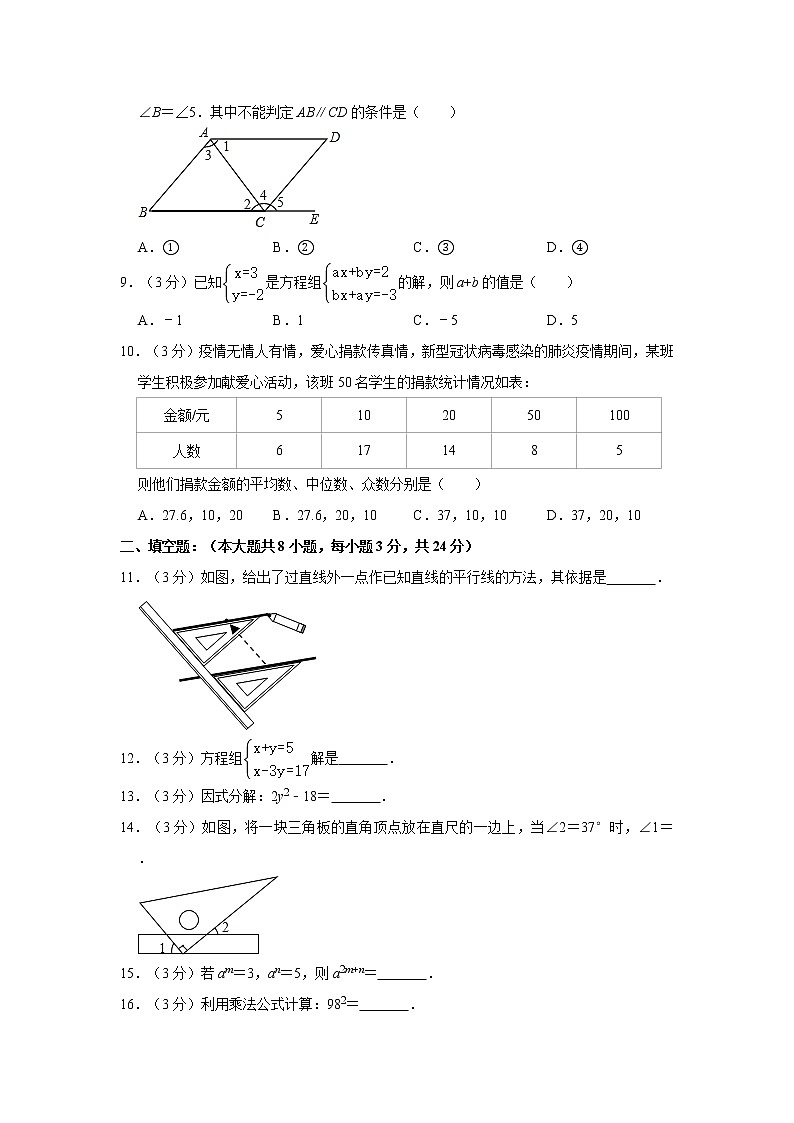
8.(3分)如图,有以下四个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5.其中不能判定AB∥CD的条件是( )
A.① B.② C.③ D.④
9.(3分)已知是方程组的解,则a+b的值是( )
A.﹣1 B.1 C.﹣5 D.5
10.(3分)疫情无情人有情,爱心捐款传真情,新型冠状病毒感染的肺炎疫情期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如表:
金额/元
5
10
20
50
100
人数
6
17
14
8
5
则他们捐款金额的平均数、中位数、众数分别是( )
A.27.6,10,20 B.27.6,20,10 C.37,10,10 D.37,20,10
二、填空题:(本大题共8小题,每小题3分,共24分)
11.(3分)如图,给出了过直线外一点作已知直线的平行线的方法,其依据是 .
12.(3分)方程组解是 .
13.(3分)因式分解:2y2﹣18= .
14.(3分)如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=37°时,∠1= .
15.(3分)若am=3,an=5,则a2m+n= .
16.(3分)利用乘法公式计算:982= .
17.(3分)如图所示,△COD是△AOB绕点O顺时针方向旋转35°后所得的图形,点C恰好在AB上,∠AOD=90°,则∠BOC的度数是 .
18.(3分)如图,把一张长方形纸条ABCD沿EF折叠,若∠BGD'为x度,则∠1的度数应为 度(用含x的代数式表示).
三、解答题(共6分)
19.(8分)(1)解方程组:;
(2)计算:(x+1)(2x﹣3).
20.(8分)把下列多项式因式分解:
(1)x(y﹣3)﹣(2y﹣6);
(2)﹣4ax2+12ax﹣9a.
21.(6分)先化简,再求值:(x﹣2y)2+(x﹣2y)(x+2y),其中x=﹣2,y=1.
22.(8分)如图,在边长为1的小正方形组成的网格中,△OAB的顶点都在格点上.
(1)请作出△OAB关于直线CD对称的△O1A1B1;
(2)请将△OAB绕点B顺时针旋转90°,画出旋转后的△BO2A2.
23.(8分)如图,直线a∥b,AB与a,b分别相交于点A,B,且AC⊥AB,AC交直线b于点C.
(1)若∠1=60°,求∠2的度数;
(2)若AC=5,AB=12,BC=13,求直线a与b的距离.
24.(8分)从A地到B地全程290千米,前一路段为国道,其余路段为高速公路.已知汽车在国道上行驶的速度为60km/h,在高速公路上行驶的速度为100km/h,一辆客车从A地开往B地一共行驶了3.5h.求A、B两地间国道和高速公路各多少千米?
25.(10分)我市某中学举行“校园好声音”歌手大赛,高、初中根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩(满分100)如图所示:
根据图示信息,整理分析数据如表:
平均数(分)
中位数(分)
众数(分)
初中部
a
85
c
高中部
85
b
100
(1)求出表格中a= ;b= ;c= .
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)小明同学已经算出高中代表队决赛成绩的方差是:s=[(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160;
请你计算出初中代表队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.
26.(10分)【问题情境】:
如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,求∠APC的度数;
【问题迁移】:
如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
【问题应用】:
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
2019-2020学年湖南省邵阳市邵东县七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)请将正确答案的代号填写在答题卡上.
1.(3分)如下字体的四个汉字中,可以看作是轴对称图形的是( )
A.中 B.国 C.加 D.油
【分析】根据轴对称图形的概念求解.
【解答】解:A、“中”可以看作是轴对称图形,故本选项符合题意;
B、“国”不是轴对称图形,故本选项不合题意;
C、“加”不是轴对称图形,故本选项不合题意;
D、“油”不是轴对称图形,故本选项不合题意.
故选:A.
2.(3分)如图,已知∠1=65°,如果CD∥BE,那么∠B的度数为( )
A.65° B.105° C.115° D.125°
【分析】先求出∠1的对顶角,再根据两直线平行,同旁内角互补即可求出.
【解答】解:如图,∵∠1=70°,
∴∠2=∠1=70°,
∵CD∥BE,
∴∠B=180°﹣∠2=180°﹣65°=115°.
故选:C.
3.(3分)下列运算正确的是( )
A.a2+a3=2a5 B.(a﹣b)2=a2﹣b2
C.a3•a5=a15 D.(ab2)2=a2b4
【分析】直接利用完全平方公式、同底数幂的乘法运算法则和积的乘方运算法则、合并同类项法则分别判断求出答案.
【解答】解:A、a2和a3不是同类项,不能合并,故此选项错误;
B、(a﹣b)2=a2﹣2ab+b2,故此选项错误;
C、a3•a5=a8,故此选项错误;
D、(ab2)2=a2b4,故此选项正确.
故选:D.
4.(3分)下列各式中,不能够用平方差公式计算的是( )
A.( y+2x)(2x﹣y) B.(﹣x﹣3y)(x+3y)
C.(2x2﹣y2 )(2x2+y2 ) D.(4a+b﹣c)(4a﹣b﹣c)
【分析】运用平方差公式(a+b)(a﹣b)=a2﹣b2时,关键要找相同项和相反项,其结果是相同项的平方减去相反项的平方.
【解答】解:B、两项都是相反项的项,不能运用平方差公式;
A、C、D中均存在相同和相反的项,
故选:B.
5.(3分)若a﹣b=1,a2+b2=13,则ab等于( )
A.6 B.7 C.﹣6 D.﹣7
【分析】将a﹣b=1两边平方,利用完全平方公式化简,将第一个等式代入计算即可求出ab的值.
【解答】解:将a﹣b=1两边平方得:(a﹣b)2=a2+b2﹣2ab=1,
把a2+b2=13代入得:13﹣2ab=1,
解得:ab=6.
故选:A.
6.(3分)《九章算术》中记载:“今有人共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”意思是:现在一些人共同买一个物品,每人出8元,还余3元;每人出7元,还差4元.问共有多少人?这个物品价格是多少元?设共有x个人,这个物品价格是y元.则可列方程组为( )
A. B.
C. D.
【分析】设共有x个人,这个物品价格是y元,根据物品的价格不变列出方程.
【解答】解:设共有x个人,这个物品价格是y元,则.
故选:A.
7.(3分)下列各式从左到右因式分解正确的是( )
A.2x﹣6y+2=2(x﹣3y) B.x2﹣2x+1=x(x﹣2)+1
C.x2﹣4=(x﹣2)2 D.x3﹣x=x(x+1)(x﹣1)
【分析】直接利用公式法以及提取公因式法分解因式进而得出答案.
【解答】解:A、2x﹣6y+2=2(x﹣3y+1),故原式分解因式错误,不合题意;
B、x2﹣2x+1=(x﹣1)2,故原式分解因式错误,不合题意;
C、x2﹣4=(x+2)(x﹣2),故原式分解因式错误,不合题意;
D、x3﹣x=x(x+1)(x﹣1),正确.
故选:D.
8.(3分)如图,有以下四个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5.其中不能判定AB∥CD的条件是( )
A.① B.② C.③ D.④
【分析】根据平行线的判定定理求解,即可求得答案.
【解答】解:①∵∠B+∠BCD=180°,
∴AB∥CD;
②∵∠1=∠2,
∴AD∥BC;
③∵∠3=∠4,
∴AB∥CD;
④∵∠B=∠5,
∴AB∥CD;
∴能得到AB∥CD的条件是①③④.
故选:B.
9.(3分)已知是方程组的解,则a+b的值是( )
A.﹣1 B.1 C.﹣5 D.5
【分析】根据二元一次方程组的解法即可求出答案.
【解答】解:将代入,
可得:,
两式相加:a+b=﹣1,
故选:A.
10.(3分)疫情无情人有情,爱心捐款传真情,新型冠状病毒感染的肺炎疫情期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如表:
金额/元
5
10
20
50
100
人数
6
17
14
8
5
则他们捐款金额的平均数、中位数、众数分别是( )
A.27.6,10,20 B.27.6,20,10 C.37,10,10 D.37,20,10
【分析】根据平均数的计算公式求出这组数据的平均数,再根据中位数的定义直接求出这组数据的中位数即可.
【解答】解:这组数的平均数是×(5×6+10×17+20×14+50×8+100×5)=27.6;
把这些数从小到大排列,最中间两个数的平均数=20,
这组数据中,10 出现次数17次,故众数为10.
故选:B.
二、填空题:(本大题共8小题,每小题3分,共24分)
11.(3分)如图,给出了过直线外一点作已知直线的平行线的方法,其依据是 同位角相等,两直线平行 .
【分析】利用作图可得,画出两同位角相等,从而根据平行线的判定方法可判断所画直线与原直线平行.
【解答】解:给出了过直线外一点作已知直线的平行线的方法,其依据是同位角相等,两直线平行.
故答案为同位角相等,两直线平行.
12.(3分)方程组解是 .
【分析】利用加减消元法求解可得.
【解答】解:,
①﹣②,得:4y=﹣12,
解得y=﹣3,
将y=﹣3代入①,得:x﹣3=5,
解得x=8,
所以方程组的解为,
故答案为:.
13.(3分)因式分解:2y2﹣18= 2(y+3)(y﹣3) .
【分析】原式提取2,再利用平方差公式分解即可.
【解答】解:原式=2(y2﹣9)=2(y+3)(y﹣3),
故答案为:2(y+3)(y﹣3)
14.(3分)如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=37°时,∠1= 53° .
【分析】由平行线的性质求出∠2=∠3=37°,根据平角的定义,垂直的定义,角的和差求得∠1=53°.
【解答】解:如图所示:
∵a∥b,
∴∠2=∠3,
又∵∠2=37°,
∴∠3=37°,
又∵∠1+∠3+∠4=180°,∠4=90°,
∴∠1=53°,
故答案为53°.
15.(3分)若am=3,an=5,则a2m+n= 45 .
【分析】把a2m+n化为(am)2•an,再利用am=3,an=5计算求解.
【解答】解:∵am=3,an=5,
∴a2m+n=(am)2•an=9×5=45,
故答案为:45.
16.(3分)利用乘法公式计算:982= 9604 .
【分析】把98写成(100﹣2),再利用完全平方公式计算即可
【解答】解:982
=(100﹣2)2
=1002﹣2×100×2+22
=10000﹣400+4
=9604.
故答案为:9604.
17.(3分)如图所示,△COD是△AOB绕点O顺时针方向旋转35°后所得的图形,点C恰好在AB上,∠AOD=90°,则∠BOC的度数是 20° .
【分析】由旋转的性质可得∠AOC=∠BOD=35°,即可求解.
【解答】解:∵△COD是△AOB绕点O顺时针方向旋转35°后所得的图形,
∴∠AOC=∠BOD=35°,且∠AOD=90°,
∴∠BOC=20°,
故答案为20°
18.(3分)如图,把一张长方形纸条ABCD沿EF折叠,若∠BGD'为x度,则∠1的度数应为 度(用含x的代数式表示).
【分析】此题要求∠AEG的度数,只需求得其邻补角的度数,根据平行线的性质以及折叠的性质就可求解.
【解答】解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠DEF=∠1,∠AED′=∠BGD'=x度,
再根据对折,得:∠GEF=∠DEF,
再根据平角的定义,得:∠DEF=(180°﹣x°)÷2=度.
∴∠1=度.
故答案为:.
三、解答题(共6分)
19.(8分)(1)解方程组:;
(2)计算:(x+1)(2x﹣3).
【分析】(1)首先①×2得:4x﹣2y=2③,再利用②+③可消去y求出x的值,然后再代入①可得y的值,进而可得方程组的解;
(2)利用多项式乘以多项式计算法则进行计算即可.
【解答】解:(1),
①×2得:4x﹣2y=2③,
②+③得:7x=14,
解得:x=2,
把x=2代入①得:y=3,
∴方程组的解为;
(2)原式=2x2﹣3x+2x﹣3=2x2﹣x﹣3.
20.(8分)把下列多项式因式分解:
(1)x(y﹣3)﹣(2y﹣6);
(2)﹣4ax2+12ax﹣9a.
【分析】(1)原式整理后,提取公因式即可;
(2)原式提取公因式,再利用完全平方公式分解即可.
【解答】解:(1)原式=x(y﹣3)﹣2(y﹣3)
=(y﹣3)(x﹣2);
(2)原式=﹣a(4x2﹣12x+9)
=﹣a(2x﹣3)2.
21.(6分)先化简,再求值:(x﹣2y)2+(x﹣2y)(x+2y),其中x=﹣2,y=1.
【分析】根据整式的运算法则即可求出答案.
【解答】解:原式=(x﹣2y)(x﹣2y+x+2y)
=2x(x﹣2y)
=2x2﹣4xy,
当x=﹣2,y=1时,
原式=2×4﹣4×(﹣2)×1
=8+8
=16.
22.(8分)如图,在边长为1的小正方形组成的网格中,△OAB的顶点都在格点上.
(1)请作出△OAB关于直线CD对称的△O1A1B1;
(2)请将△OAB绕点B顺时针旋转90°,画出旋转后的△BO2A2.
【分析】(1)△OAB关于直线CD对称的△O1A1B1在CD的右侧,对应点到CD的距离相等;
(2)将△OAB的三个顶点分别绕点B顺时针旋转90°,再顺次连接所得的三个顶点可得旋转后的△BO2A2.
【解答】解:(1)如图所示,△O1A1B1即为所求;
(2)如图所示,△BO2A2即为所求.
23.(8分)如图,直线a∥b,AB与a,b分别相交于点A,B,且AC⊥AB,AC交直线b于点C.
(1)若∠1=60°,求∠2的度数;
(2)若AC=5,AB=12,BC=13,求直线a与b的距离.
【分析】(1)由直线a∥b,根据平行线的性质得出∠3=∠1=60°,再由AC⊥AB,根据垂直的定义即可得到∠2=90°﹣∠3=30°;
(2)过A作AD⊥BC于D,依据S△ABC=×AB×AC=×BC×AD,即可求出AD.
【解答】解:(1)∵直线a∥b,
∴∠3=∠1=60°,
又∵AC⊥AB,
∴∠2=90°﹣∠3=30°;
(2)如图,过A作AD⊥BC于D,则AD的长即为直线a与b的距离.
∵S△ABC=×AB×AC=×BC×AD,
∴AD===,
∴直线a与b的距离为.
24.(8分)从A地到B地全程290千米,前一路段为国道,其余路段为高速公路.已知汽车在国道上行驶的速度为60km/h,在高速公路上行驶的速度为100km/h,一辆客车从A地开往B地一共行驶了3.5h.求A、B两地间国道和高速公路各多少千米?
【分析】首先设A、B两地间国道和高速公路分别是x、y千米,根据题意可得等量关系:国道路程+高速路程=290,在国道上行驶的时间+在高速公路上行驶的时间=3.5,根据等量关系列出方程组,再解即可.
【解答】解:设A、B两地间国道和高速公路分别是x、y千米,依题意得:
,
解得,
答:A、B两地间国道和高速公路分别是90、200千米.
25.(10分)我市某中学举行“校园好声音”歌手大赛,高、初中根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩(满分100)如图所示:
根据图示信息,整理分析数据如表:
平均数(分)
中位数(分)
众数(分)
初中部
a
85
c
高中部
85
b
100
(1)求出表格中a= 85 ;b= 80 ;c= 85 .
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)小明同学已经算出高中代表队决赛成绩的方差是:s=[(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160;
请你计算出初中代表队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.
【分析】(1)根据平均数、中位数和众数的定义求解;
(2)利用中位数的意义进行判断;
(3)先利用方差公式计算出初中代表队决赛成绩的方差,然后比较两队的方差,根据方差的意义进行判断.
【解答】解:(1)a=(75+80+85+85+100)=85;
b=80,c=85;
故答案为85;80;85;
(2)两队成绩的平均数相同,但初中代表队的成绩的中位数大,所以初中代表队的决赛成绩较好;
(3)S2初中=[(75﹣85)2+(80﹣85)2+(85﹣85)2+(85﹣85)2+(100﹣85)2]=70;
因为S2初中=<S2高中,
所以初中代表队选手成绩较为稳定.
26.(10分)【问题情境】:
如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,求∠APC的度数;
【问题迁移】:
如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
【问题应用】:
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
【分析】(1)过P作PE∥AB,通过平行线性质可得∠A+∠APE=180°,∠C+∠CPE=180°再代入∠PAB=130°,∠PCD=120°可求∠APC即可;
(2)过P作PE∥AD交AC于E,推出AB∥PE∥DC,根据平行线的性质得出∠α=∠APE,∠β=∠CPE,即可得出答案;
(3)分两种情况:P在BD延长线上;P在DB延长线上,分别画出图形,根据平行线的性质得出∠α=∠APE,∠β=∠CPE,即可得出答案.
【解答】(1)解:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
(2)∠APC=∠α+∠β,
理由:如图2,过P作PE∥AB交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图所示,当P在BD延长线上时,
∠CPA=∠α﹣∠β;
如图所示,当P在DB延长线上时,
∠CPA=∠β﹣∠α.
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)请将正确答案的代号填写在答题卡上.
1.(3分)如下字体的四个汉字中,可以看作是轴对称图形的是( )
A.中 B.国 C.加 D.油
2.(3分)如图,已知∠1=65°,如果CD∥BE,那么∠B的度数为( )
A.65° B.105° C.115° D.125°
3.(3分)下列运算正确的是( )
A.a2+a3=2a5 B.(a﹣b)2=a2﹣b2
C.a3•a5=a15 D.(ab2)2=a2b4
4.(3分)下列各式中,不能够用平方差公式计算的是( )
A.( y+2x)(2x﹣y) B.(﹣x﹣3y)(x+3y)
C.(2x2﹣y2 )(2x2+y2 ) D.(4a+b﹣c)(4a﹣b﹣c)
5.(3分)若a﹣b=1,a2+b2=13,则ab等于( )
A.6 B.7 C.﹣6 D.﹣7
6.(3分)《九章算术》中记载:“今有人共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”意思是:现在一些人共同买一个物品,每人出8元,还余3元;每人出7元,还差4元.问共有多少人?这个物品价格是多少元?设共有x个人,这个物品价格是y元.则可列方程组为( )
A. B.
C. D.
7.(3分)下列各式从左到右因式分解正确的是( )
A.2x﹣6y+2=2(x﹣3y) B.x2﹣2x+1=x(x﹣2)+1
C.x2﹣4=(x﹣2)2 D.x3﹣x=x(x+1)(x﹣1)
8.(3分)如图,有以下四个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5.其中不能判定AB∥CD的条件是( )
A.① B.② C.③ D.④
9.(3分)已知是方程组的解,则a+b的值是( )
A.﹣1 B.1 C.﹣5 D.5
10.(3分)疫情无情人有情,爱心捐款传真情,新型冠状病毒感染的肺炎疫情期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如表:
金额/元
5
10
20
50
100
人数
6
17
14
8
5
则他们捐款金额的平均数、中位数、众数分别是( )
A.27.6,10,20 B.27.6,20,10 C.37,10,10 D.37,20,10
二、填空题:(本大题共8小题,每小题3分,共24分)
11.(3分)如图,给出了过直线外一点作已知直线的平行线的方法,其依据是 .
12.(3分)方程组解是 .
13.(3分)因式分解:2y2﹣18= .
14.(3分)如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=37°时,∠1= .
15.(3分)若am=3,an=5,则a2m+n= .
16.(3分)利用乘法公式计算:982= .
17.(3分)如图所示,△COD是△AOB绕点O顺时针方向旋转35°后所得的图形,点C恰好在AB上,∠AOD=90°,则∠BOC的度数是 .
18.(3分)如图,把一张长方形纸条ABCD沿EF折叠,若∠BGD'为x度,则∠1的度数应为 度(用含x的代数式表示).
三、解答题(共6分)
19.(8分)(1)解方程组:;
(2)计算:(x+1)(2x﹣3).
20.(8分)把下列多项式因式分解:
(1)x(y﹣3)﹣(2y﹣6);
(2)﹣4ax2+12ax﹣9a.
21.(6分)先化简,再求值:(x﹣2y)2+(x﹣2y)(x+2y),其中x=﹣2,y=1.
22.(8分)如图,在边长为1的小正方形组成的网格中,△OAB的顶点都在格点上.
(1)请作出△OAB关于直线CD对称的△O1A1B1;
(2)请将△OAB绕点B顺时针旋转90°,画出旋转后的△BO2A2.
23.(8分)如图,直线a∥b,AB与a,b分别相交于点A,B,且AC⊥AB,AC交直线b于点C.
(1)若∠1=60°,求∠2的度数;
(2)若AC=5,AB=12,BC=13,求直线a与b的距离.
24.(8分)从A地到B地全程290千米,前一路段为国道,其余路段为高速公路.已知汽车在国道上行驶的速度为60km/h,在高速公路上行驶的速度为100km/h,一辆客车从A地开往B地一共行驶了3.5h.求A、B两地间国道和高速公路各多少千米?
25.(10分)我市某中学举行“校园好声音”歌手大赛,高、初中根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩(满分100)如图所示:
根据图示信息,整理分析数据如表:
平均数(分)
中位数(分)
众数(分)
初中部
a
85
c
高中部
85
b
100
(1)求出表格中a= ;b= ;c= .
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)小明同学已经算出高中代表队决赛成绩的方差是:s=[(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160;
请你计算出初中代表队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.
26.(10分)【问题情境】:
如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,求∠APC的度数;
【问题迁移】:
如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
【问题应用】:
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
2019-2020学年湖南省邵阳市邵东县七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)请将正确答案的代号填写在答题卡上.
1.(3分)如下字体的四个汉字中,可以看作是轴对称图形的是( )
A.中 B.国 C.加 D.油
【分析】根据轴对称图形的概念求解.
【解答】解:A、“中”可以看作是轴对称图形,故本选项符合题意;
B、“国”不是轴对称图形,故本选项不合题意;
C、“加”不是轴对称图形,故本选项不合题意;
D、“油”不是轴对称图形,故本选项不合题意.
故选:A.
2.(3分)如图,已知∠1=65°,如果CD∥BE,那么∠B的度数为( )
A.65° B.105° C.115° D.125°
【分析】先求出∠1的对顶角,再根据两直线平行,同旁内角互补即可求出.
【解答】解:如图,∵∠1=70°,
∴∠2=∠1=70°,
∵CD∥BE,
∴∠B=180°﹣∠2=180°﹣65°=115°.
故选:C.
3.(3分)下列运算正确的是( )
A.a2+a3=2a5 B.(a﹣b)2=a2﹣b2
C.a3•a5=a15 D.(ab2)2=a2b4
【分析】直接利用完全平方公式、同底数幂的乘法运算法则和积的乘方运算法则、合并同类项法则分别判断求出答案.
【解答】解:A、a2和a3不是同类项,不能合并,故此选项错误;
B、(a﹣b)2=a2﹣2ab+b2,故此选项错误;
C、a3•a5=a8,故此选项错误;
D、(ab2)2=a2b4,故此选项正确.
故选:D.
4.(3分)下列各式中,不能够用平方差公式计算的是( )
A.( y+2x)(2x﹣y) B.(﹣x﹣3y)(x+3y)
C.(2x2﹣y2 )(2x2+y2 ) D.(4a+b﹣c)(4a﹣b﹣c)
【分析】运用平方差公式(a+b)(a﹣b)=a2﹣b2时,关键要找相同项和相反项,其结果是相同项的平方减去相反项的平方.
【解答】解:B、两项都是相反项的项,不能运用平方差公式;
A、C、D中均存在相同和相反的项,
故选:B.
5.(3分)若a﹣b=1,a2+b2=13,则ab等于( )
A.6 B.7 C.﹣6 D.﹣7
【分析】将a﹣b=1两边平方,利用完全平方公式化简,将第一个等式代入计算即可求出ab的值.
【解答】解:将a﹣b=1两边平方得:(a﹣b)2=a2+b2﹣2ab=1,
把a2+b2=13代入得:13﹣2ab=1,
解得:ab=6.
故选:A.
6.(3分)《九章算术》中记载:“今有人共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”意思是:现在一些人共同买一个物品,每人出8元,还余3元;每人出7元,还差4元.问共有多少人?这个物品价格是多少元?设共有x个人,这个物品价格是y元.则可列方程组为( )
A. B.
C. D.
【分析】设共有x个人,这个物品价格是y元,根据物品的价格不变列出方程.
【解答】解:设共有x个人,这个物品价格是y元,则.
故选:A.
7.(3分)下列各式从左到右因式分解正确的是( )
A.2x﹣6y+2=2(x﹣3y) B.x2﹣2x+1=x(x﹣2)+1
C.x2﹣4=(x﹣2)2 D.x3﹣x=x(x+1)(x﹣1)
【分析】直接利用公式法以及提取公因式法分解因式进而得出答案.
【解答】解:A、2x﹣6y+2=2(x﹣3y+1),故原式分解因式错误,不合题意;
B、x2﹣2x+1=(x﹣1)2,故原式分解因式错误,不合题意;
C、x2﹣4=(x+2)(x﹣2),故原式分解因式错误,不合题意;
D、x3﹣x=x(x+1)(x﹣1),正确.
故选:D.
8.(3分)如图,有以下四个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5.其中不能判定AB∥CD的条件是( )
A.① B.② C.③ D.④
【分析】根据平行线的判定定理求解,即可求得答案.
【解答】解:①∵∠B+∠BCD=180°,
∴AB∥CD;
②∵∠1=∠2,
∴AD∥BC;
③∵∠3=∠4,
∴AB∥CD;
④∵∠B=∠5,
∴AB∥CD;
∴能得到AB∥CD的条件是①③④.
故选:B.
9.(3分)已知是方程组的解,则a+b的值是( )
A.﹣1 B.1 C.﹣5 D.5
【分析】根据二元一次方程组的解法即可求出答案.
【解答】解:将代入,
可得:,
两式相加:a+b=﹣1,
故选:A.
10.(3分)疫情无情人有情,爱心捐款传真情,新型冠状病毒感染的肺炎疫情期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如表:
金额/元
5
10
20
50
100
人数
6
17
14
8
5
则他们捐款金额的平均数、中位数、众数分别是( )
A.27.6,10,20 B.27.6,20,10 C.37,10,10 D.37,20,10
【分析】根据平均数的计算公式求出这组数据的平均数,再根据中位数的定义直接求出这组数据的中位数即可.
【解答】解:这组数的平均数是×(5×6+10×17+20×14+50×8+100×5)=27.6;
把这些数从小到大排列,最中间两个数的平均数=20,
这组数据中,10 出现次数17次,故众数为10.
故选:B.
二、填空题:(本大题共8小题,每小题3分,共24分)
11.(3分)如图,给出了过直线外一点作已知直线的平行线的方法,其依据是 同位角相等,两直线平行 .
【分析】利用作图可得,画出两同位角相等,从而根据平行线的判定方法可判断所画直线与原直线平行.
【解答】解:给出了过直线外一点作已知直线的平行线的方法,其依据是同位角相等,两直线平行.
故答案为同位角相等,两直线平行.
12.(3分)方程组解是 .
【分析】利用加减消元法求解可得.
【解答】解:,
①﹣②,得:4y=﹣12,
解得y=﹣3,
将y=﹣3代入①,得:x﹣3=5,
解得x=8,
所以方程组的解为,
故答案为:.
13.(3分)因式分解:2y2﹣18= 2(y+3)(y﹣3) .
【分析】原式提取2,再利用平方差公式分解即可.
【解答】解:原式=2(y2﹣9)=2(y+3)(y﹣3),
故答案为:2(y+3)(y﹣3)
14.(3分)如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=37°时,∠1= 53° .
【分析】由平行线的性质求出∠2=∠3=37°,根据平角的定义,垂直的定义,角的和差求得∠1=53°.
【解答】解:如图所示:
∵a∥b,
∴∠2=∠3,
又∵∠2=37°,
∴∠3=37°,
又∵∠1+∠3+∠4=180°,∠4=90°,
∴∠1=53°,
故答案为53°.
15.(3分)若am=3,an=5,则a2m+n= 45 .
【分析】把a2m+n化为(am)2•an,再利用am=3,an=5计算求解.
【解答】解:∵am=3,an=5,
∴a2m+n=(am)2•an=9×5=45,
故答案为:45.
16.(3分)利用乘法公式计算:982= 9604 .
【分析】把98写成(100﹣2),再利用完全平方公式计算即可
【解答】解:982
=(100﹣2)2
=1002﹣2×100×2+22
=10000﹣400+4
=9604.
故答案为:9604.
17.(3分)如图所示,△COD是△AOB绕点O顺时针方向旋转35°后所得的图形,点C恰好在AB上,∠AOD=90°,则∠BOC的度数是 20° .
【分析】由旋转的性质可得∠AOC=∠BOD=35°,即可求解.
【解答】解:∵△COD是△AOB绕点O顺时针方向旋转35°后所得的图形,
∴∠AOC=∠BOD=35°,且∠AOD=90°,
∴∠BOC=20°,
故答案为20°
18.(3分)如图,把一张长方形纸条ABCD沿EF折叠,若∠BGD'为x度,则∠1的度数应为 度(用含x的代数式表示).
【分析】此题要求∠AEG的度数,只需求得其邻补角的度数,根据平行线的性质以及折叠的性质就可求解.
【解答】解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠DEF=∠1,∠AED′=∠BGD'=x度,
再根据对折,得:∠GEF=∠DEF,
再根据平角的定义,得:∠DEF=(180°﹣x°)÷2=度.
∴∠1=度.
故答案为:.
三、解答题(共6分)
19.(8分)(1)解方程组:;
(2)计算:(x+1)(2x﹣3).
【分析】(1)首先①×2得:4x﹣2y=2③,再利用②+③可消去y求出x的值,然后再代入①可得y的值,进而可得方程组的解;
(2)利用多项式乘以多项式计算法则进行计算即可.
【解答】解:(1),
①×2得:4x﹣2y=2③,
②+③得:7x=14,
解得:x=2,
把x=2代入①得:y=3,
∴方程组的解为;
(2)原式=2x2﹣3x+2x﹣3=2x2﹣x﹣3.
20.(8分)把下列多项式因式分解:
(1)x(y﹣3)﹣(2y﹣6);
(2)﹣4ax2+12ax﹣9a.
【分析】(1)原式整理后,提取公因式即可;
(2)原式提取公因式,再利用完全平方公式分解即可.
【解答】解:(1)原式=x(y﹣3)﹣2(y﹣3)
=(y﹣3)(x﹣2);
(2)原式=﹣a(4x2﹣12x+9)
=﹣a(2x﹣3)2.
21.(6分)先化简,再求值:(x﹣2y)2+(x﹣2y)(x+2y),其中x=﹣2,y=1.
【分析】根据整式的运算法则即可求出答案.
【解答】解:原式=(x﹣2y)(x﹣2y+x+2y)
=2x(x﹣2y)
=2x2﹣4xy,
当x=﹣2,y=1时,
原式=2×4﹣4×(﹣2)×1
=8+8
=16.
22.(8分)如图,在边长为1的小正方形组成的网格中,△OAB的顶点都在格点上.
(1)请作出△OAB关于直线CD对称的△O1A1B1;
(2)请将△OAB绕点B顺时针旋转90°,画出旋转后的△BO2A2.
【分析】(1)△OAB关于直线CD对称的△O1A1B1在CD的右侧,对应点到CD的距离相等;
(2)将△OAB的三个顶点分别绕点B顺时针旋转90°,再顺次连接所得的三个顶点可得旋转后的△BO2A2.
【解答】解:(1)如图所示,△O1A1B1即为所求;
(2)如图所示,△BO2A2即为所求.
23.(8分)如图,直线a∥b,AB与a,b分别相交于点A,B,且AC⊥AB,AC交直线b于点C.
(1)若∠1=60°,求∠2的度数;
(2)若AC=5,AB=12,BC=13,求直线a与b的距离.
【分析】(1)由直线a∥b,根据平行线的性质得出∠3=∠1=60°,再由AC⊥AB,根据垂直的定义即可得到∠2=90°﹣∠3=30°;
(2)过A作AD⊥BC于D,依据S△ABC=×AB×AC=×BC×AD,即可求出AD.
【解答】解:(1)∵直线a∥b,
∴∠3=∠1=60°,
又∵AC⊥AB,
∴∠2=90°﹣∠3=30°;
(2)如图,过A作AD⊥BC于D,则AD的长即为直线a与b的距离.
∵S△ABC=×AB×AC=×BC×AD,
∴AD===,
∴直线a与b的距离为.
24.(8分)从A地到B地全程290千米,前一路段为国道,其余路段为高速公路.已知汽车在国道上行驶的速度为60km/h,在高速公路上行驶的速度为100km/h,一辆客车从A地开往B地一共行驶了3.5h.求A、B两地间国道和高速公路各多少千米?
【分析】首先设A、B两地间国道和高速公路分别是x、y千米,根据题意可得等量关系:国道路程+高速路程=290,在国道上行驶的时间+在高速公路上行驶的时间=3.5,根据等量关系列出方程组,再解即可.
【解答】解:设A、B两地间国道和高速公路分别是x、y千米,依题意得:
,
解得,
答:A、B两地间国道和高速公路分别是90、200千米.
25.(10分)我市某中学举行“校园好声音”歌手大赛,高、初中根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩(满分100)如图所示:
根据图示信息,整理分析数据如表:
平均数(分)
中位数(分)
众数(分)
初中部
a
85
c
高中部
85
b
100
(1)求出表格中a= 85 ;b= 80 ;c= 85 .
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)小明同学已经算出高中代表队决赛成绩的方差是:s=[(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160;
请你计算出初中代表队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.
【分析】(1)根据平均数、中位数和众数的定义求解;
(2)利用中位数的意义进行判断;
(3)先利用方差公式计算出初中代表队决赛成绩的方差,然后比较两队的方差,根据方差的意义进行判断.
【解答】解:(1)a=(75+80+85+85+100)=85;
b=80,c=85;
故答案为85;80;85;
(2)两队成绩的平均数相同,但初中代表队的成绩的中位数大,所以初中代表队的决赛成绩较好;
(3)S2初中=[(75﹣85)2+(80﹣85)2+(85﹣85)2+(85﹣85)2+(100﹣85)2]=70;
因为S2初中=<S2高中,
所以初中代表队选手成绩较为稳定.
26.(10分)【问题情境】:
如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,求∠APC的度数;
【问题迁移】:
如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
【问题应用】:
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
【分析】(1)过P作PE∥AB,通过平行线性质可得∠A+∠APE=180°,∠C+∠CPE=180°再代入∠PAB=130°,∠PCD=120°可求∠APC即可;
(2)过P作PE∥AD交AC于E,推出AB∥PE∥DC,根据平行线的性质得出∠α=∠APE,∠β=∠CPE,即可得出答案;
(3)分两种情况:P在BD延长线上;P在DB延长线上,分别画出图形,根据平行线的性质得出∠α=∠APE,∠β=∠CPE,即可得出答案.
【解答】(1)解:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
(2)∠APC=∠α+∠β,
理由:如图2,过P作PE∥AB交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图所示,当P在BD延长线上时,
∠CPA=∠α﹣∠β;
如图所示,当P在DB延长线上时,
∠CPA=∠β﹣∠α.
相关资料
更多








