初中数学人教版九年级上册第二十四章 圆综合与测试课时作业

这是一份初中数学人教版九年级上册第二十四章 圆综合与测试课时作业，共5页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

第24章 圆 单元检测试题








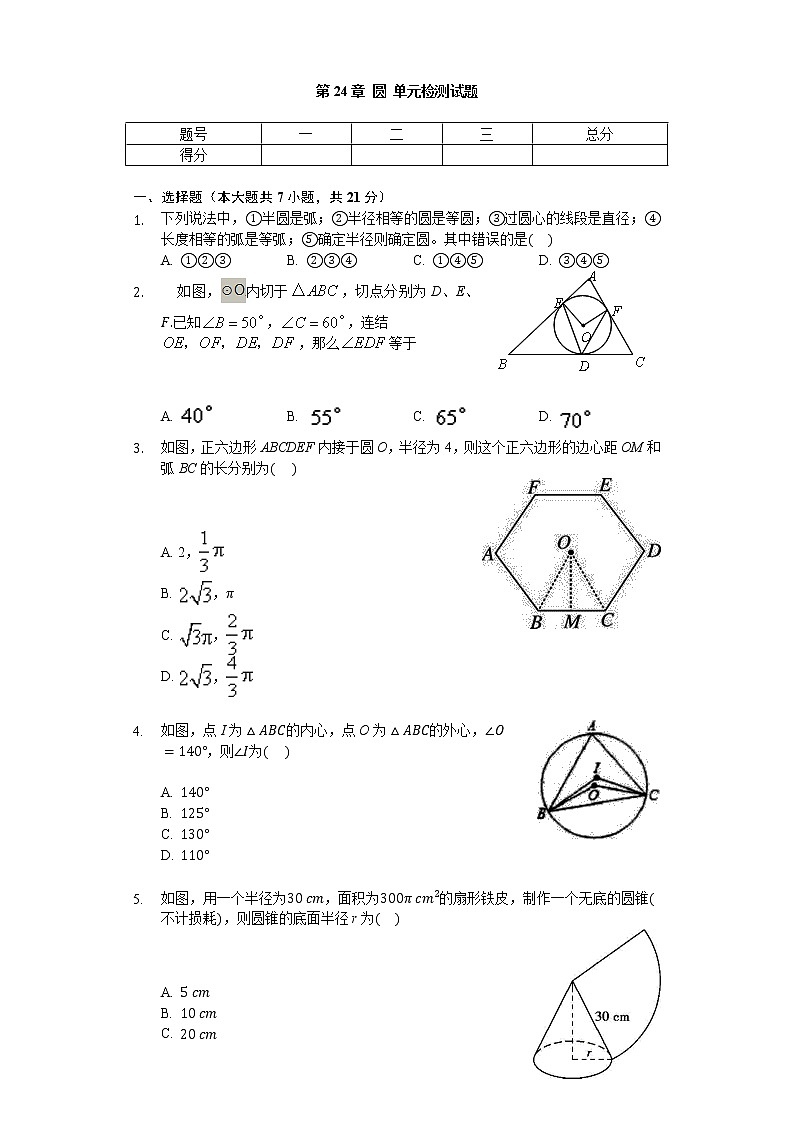
一、选择题（本大题共7小题，共21分）


下列说法中，①半圆是弧；②半径相等的圆是等圆；③过圆心的线段是直径；④长度相等的弧是等弧；⑤确定半径则确定圆。其中错误的是( )


A. ①②③B. ②③④C. ①④⑤D. ③④⑤


如图，内切于，切点分别为D、E、F.已知，，连结，那么等于








A. B. C. D.


如图，正六边形ABCDEF内接于圆O，半径为4，则这个正六边形的边心距OM和弧BC的长分别为( )





A. 2，


B. ，π


C. ，


D. ，





如图，点I为△ABC的内心，点O为△ABC的外心，∠O=140°，则∠I为( )





A. 140°


B. 125°


C. 130°


D. 110°





如图，用一个半径为30 cm，面积为300π cm2的扇形铁皮，制作一个无底的圆锥(不计损耗)，则圆锥的底面半径r为( )





A. 5 cm


B. 10 cm


C. 20 cm


D. 5π cm








一个点到圆的最大距离为11cm，最小距离为5cm，则圆的半径为( )。


A. 6cm或6cmB. 3cm或8cmC. 3cmD. 8cm


已知△ABC中，∠B≠∠C，求证：AB≠AC.若用反证法证这个结论，应首先假设()


A. ∠B=∠CB. ∠A=∠BC. AB=ACD. ∠A=∠C


二、填空题（本大题共8小题，共24分）


如图，在□ABCD中，AD=2，AB=4，∠A=30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是 (结果保留π)．





如图，点A、B、C都在⊙O上，如果∠ AOB+∠ ACB=84°，那么∠ ACB的大小是























如图，点A、B、C在⊙ O上，∠ AOC=60º，则∠ ABC= º.




















如图，AB是⊙O的直径，且经过弦CD的中点H，过CD延长线上一点E作⊙O的切线，切点为F.若∠ACF=65°，则∠E=





已知AB是直径，∠C等于15度，∠BAD的度数=

















已知⊙O的直径为8cm，直线L上一点P到圆心O的距离OP=6cm，则直线L与⊙O的位置关系是____________．


如图，△ABC中，∠ABC=50º，∠ACB=75º，点O是△ABC的内心，则∠BOC的度数为 ．





三、解答题（本大题共6小题，共78分）


如图，AB是⊙O的直径，OD⊥弦BC于点F，交⊙O于点E，连结CE、AE、CD，若∠AEC=∠ODC．


(1)求证：直线CD为⊙O的切线；


(2)若AB=5，BC=4，求线段CD的长．











如图，Rt△ABC中，∠ABC=90°，以AB为直径作半圆⊙O交AC与点D，点E为BC的中点，连接DE．


(1)求证：DE是半圆⊙O的切线．


(2)若∠BAC=30°，DE=2，求AD的长．























如图，△ABC内接于⊙O，CA=CB，CD//AB且与OA的延长线交于点D．





(1).判断CD与⊙O的位置关系并说明理由；


(2).若∠ACB=120°，OA=2，求CD的长；











已知如图，以Rt△ABC的AC边为直径作⊙O交斜边AB于点E，连接EO并延长交BC的延长线于点D，点F为BC的中点，连接EF．


(1)求证：EF是⊙O的切线．


(2)若⊙O的半径为3，∠EAC=60°，求AD的长．


























如图，在⊙O中，D，E分别是半径OA，OB的中点，点C在圆上，CD=CE.求证：AC=CB．

















如图，△ ABC内接于⊙O，∠B=60°，CD是⊙O的直径，点P是CD延长线上的一点，且AP=AC．





(1)求证：PA是⊙O的切线．


(2)若PD=，求⊙O的直径。











题号
一
二
三
总分
得分