



- 14.1.2 《幂的乘方》精品课件 课件 16 次下载
- 14.1.4 《整式的乘法》精品课件 课件 14 次下载
- 14.2.1 《平方差公式》精品课件 课件 13 次下载
- 14.2.2 《完全平方公式》精品课件 课件 11 次下载
- 14.3.1 《提公因式法》精品课件 课件 12 次下载
初中数学人教版八年级上册14.1.3 积的乘方一等奖ppt课件
展开若已知一个正方体的棱长为2×103 cm,你能计算出它的体积是多少吗?
底数是2和103的乘积,虽然103是幂,但总体来看,它是积的乘方.积的乘方如何运算呢?能不能找到一个运算法则?
是幂的乘方形式吗?
3. 掌握转化的数学思想,提高学生应用数学的意识和能力.
1. 使学生经历探索积的乘方的过程,掌握积的乘方的运算法则.
2. 能利用积的乘方的运算法则进行相应的计算和化简.
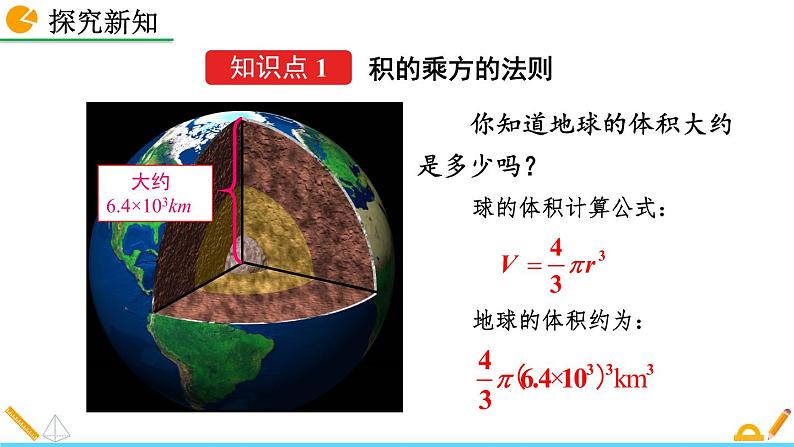
大约6.4×103km
你知道地球的体积大约是多少吗?
1.计算:(1) 10×102× 103 =______ ;(2) (x5)2=_________.
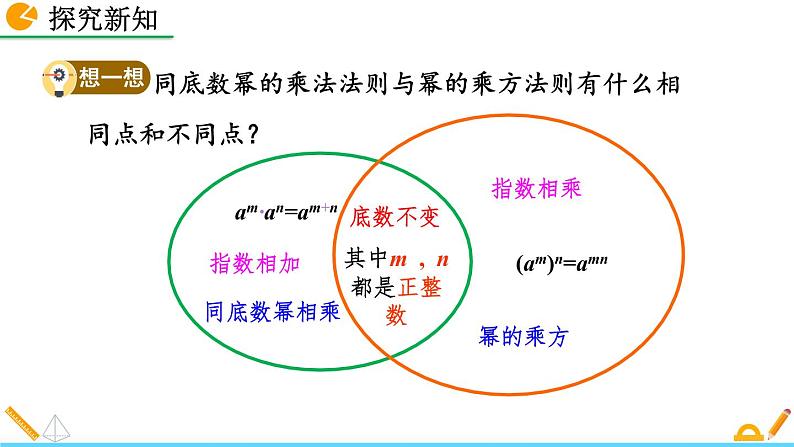
2. (1)同底数幂的乘法 :am·an= ( m,n都是正整数).
(2)幂的乘方:(am)n= (m,n都是正整数).
其中m , n都是正整数
同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?
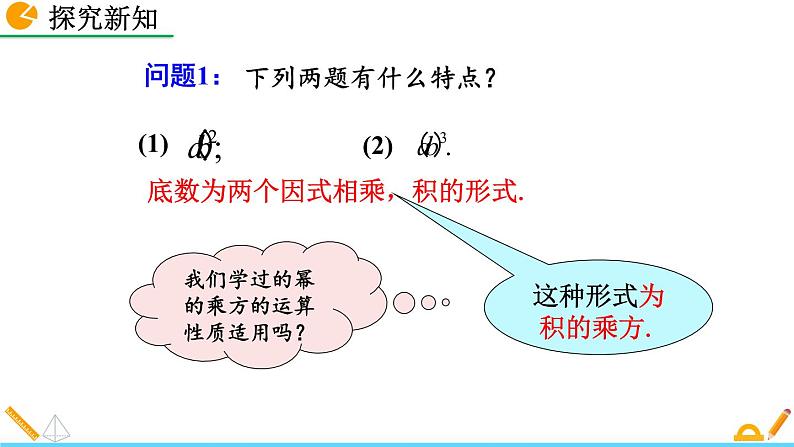
底数为两个因式相乘,积的形式.
我们学过的幂的乘方的运算性质适用吗?
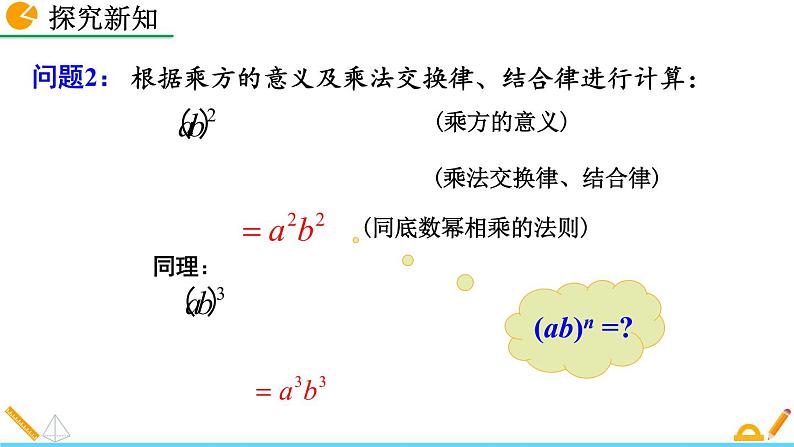
(乘法交换律、结合律)
(同底数幂相乘的法则)
根据乘方的意义及乘法交换律、结合律进行计算:
思考问题:积的乘方(ab)n =?
因此可得:(ab)n=anbn (n为正整数).
(ab)n=anbn (n为正整数)
积的乘方,等于把积的每一个因式分别_____,再把所得的幂________.
(ab)n = anbn (n为正整数)
三个或三个以上的积的乘方等于什么?
(abc)n = anbncn (n为正整数)
例1 计算: (1)(2a)3 ; (2)(–5b)3 ;(3)(xy2)2 ; (4)(–2x3)4.
方法总结:运用积的乘方法则进行计算时,注意每个因式都要乘方,尤其是字母的系数不要漏乘方.
1.计算:(1)(–5ab)3; (2)–(3x2y)2; (3)(–3ab2c3)3; (4)(–xmy3m)2.
(4)(–xmy3m)2=(–1)2x2my6m=x2my6m.
解:(1)(–5ab)3=(–5)3a3b3=–125a3b3;
(2)–(3x2y)2=–32x4y2=–9x4y2;
(3)(–3ab2c3)3=(–3)3a3b6c9=–27a3b6c9;
(2)(–3a3)2= –9a6;
(3)(–2x3y)3= –8x6y3;
(4)(–ab2)2= a2b4.
2.下面的计算对不对?如果不对,怎样改正?
(1) –4xy2·(xy2)2·(–2x2)3;(2) (–a3b6)2+(–a2b4)3.
解:(1)原式= –4xy2·x2y4·(–8x6) =[–4×(–8)]x1+2+6y2+4
(2)原式=a6b12+(–a6b12)
含有积的乘方的混合运算
=[1+(–1)]a6b12
方法总结:涉及积的乘方的混合运算,一般先算积的乘方,再算乘法,最后算加减,然后合并同类项.
如何简便计算(0.04)2004×[(–5)2004]2?
=(0.22)2004 × 54008
=(0.2)4008 × 54008
=(0.2 ×5)4008
(0.04)2004×[(–5)2004]2
=(0.04)2004 × [(–5)2]2004
=(0.04×25)2004
= (0.04)2004 ×(25)2004
①逆用积的乘方公式an·bn=(ab)n,要灵活运用,对于不符合公式的形式,要通过恒等变形,转化为公式的形式.②一般转化为底数乘积是一个正整数幂的计算较简便.
3.计算:
解析:∵2n+2n+2n+2n=2, ∴4•2n=2,∴2•2n=1,∴21+n=1, ∴1+n=0,∴n=–1.
2.下列运算正确的是( )A.(–a2)3=–a5 B.a3•a5=a15C.(–a2b3)2=a4b6 D.3a2–2a2=1
(–a2)3= –a6;
2.下列运算正确的是( ) A. x•x2=x2 B. (xy)2=xy2 C. (x2)3=x6 D. x2+x2=x4
1.计算 (–x2y)2的结果是( )A.x4y2 B.–x4y2C.x2y2 D.–x2y2
(1)(ab2)3=ab6 ( )
(2) (3xy)3=9x3y3 ( )
(3) (–2a2)2=–4a4 ( )
(4) –(–ab2)2=a2b4 ( )
4. 判断:
(1) (ab)8 ; (2) (2m)3 ; (3) (–xy)5; (4) (5ab2)3 ; (5) (2×102)2 ; (6) (–3×103)3.
解:(1)原式=a8b8;
(2)原式= 23 ·m3=8m3;
(3)原式=(–x)5 ·y5= –x5y5;
(4)原式=53 ·a3 ·(b2)3=125a3b6;
(5)原式=22 ×(102)2=4 ×104;
(6)原式=(–3)3 ×(103)3= –27 ×109= –2.7 ×1010.
(1) 2(x3)2·x3–(3x3)3+(5x)2·x7; (2)(3xy2)2+(–4xy3) · (–xy) ; (3)(–2x3)3·(x2)2.
解:原式=2x6·x3–27x9+25x2·x7 = 2x9–27x9+25x9 = 0;
解:原式=9x2y4 +4x2y4 =13x2y4;
解:原式= –8x9·x4 =–8x13.
如果(an•bm•b)3=a9b15,求m, n的值.
(an)3•(bm)3•b3=a9b15,
a 3n •b 3m•b3=a9b15 ,
a 3n •b 3m+3=a9b15,
3n=9 ,3m+3=15.
解:∵(an•bm•b)3=a9b15,
am·an=am+n (am)n=amn (ab)n=anbn ( m、n都是正整数)
am · an =am+n (am)n =amn an·bn = (ab)n可使某些计算简捷
运用积的乘方法则时要注意: 公式中的a、b代表任何代数式;每一个因式都要“乘方”;注意结果的符号、幂指数及其逆向运用(混合运算要注意运算顺序)
初中数学人教版八年级上册14.1.3 积的乘方精品课件ppt: 这是一份初中数学人教版八年级上册14.1.3 积的乘方精品课件ppt,共20页。PPT课件主要包含了知识回顾,学习目标,课堂导入,新知探究,知识点1,积的乘方,n个a,n个ab,n个b,随堂练习等内容,欢迎下载使用。
2021学年14.1.3 积的乘方获奖ppt课件: 这是一份2021学年14.1.3 积的乘方获奖ppt课件
2020-2021学年14.1.3 积的乘方优秀课件ppt: 这是一份2020-2021学年14.1.3 积的乘方优秀课件ppt














