

还剩15页未读,
继续阅读
2019-2020学年广东省云浮市郁南县七年级(下)期末数学试卷 解析版
展开
2019-2020学年广东省云浮市郁南县七年级(下)期末数学试卷
一、选择题(本大题10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的,把你认为正确选项前的字母写在答题卷对应的位置上.
1.(3分)将如图所示的图案通过平移后可以得到的图案是( )
A. B. C. D.
2.(3分)9的算术平方根是( )
A.3 B. C.9 D.±3
3.(3分)如图,直线a,b被直线c所截,a∥b,∠1=60°,则∠2的度数是( )
A.120° B.60° C.45° D.30°
4.(3分)在下列所给出坐标的点中,在第二象限的是( )
A.(2,3) B.(﹣2,3) C.(﹣2,﹣3) D.(2,﹣3)
5.(3分)不等式2x>3﹣x的解集是( )
A.x>3 B.x<3 C.x>1 D.x<1
6.(3分)已知是方程kx+y=3的一个解,那么k的值是( )
A.2 B.﹣2 C.1 D.﹣1
7.(3分)若a>b,则下列不等式正确的是( )
A.a﹣b<0 B.a+8<b﹣8 C.﹣5a<﹣5b D.
8.(3分)用加减消元法解二元一次方程组,由①﹣②可得的方程为( )
A.3x=5 B.﹣3x=9 C.﹣3x﹣6y=9 D.3x﹣6y=5
9.(3分)下列各数:0.101001…(相邻两个1之间的0的个数逐次加1),,,,,中,无理数有( )
A.1个 B.2个 C.3个 D.4个
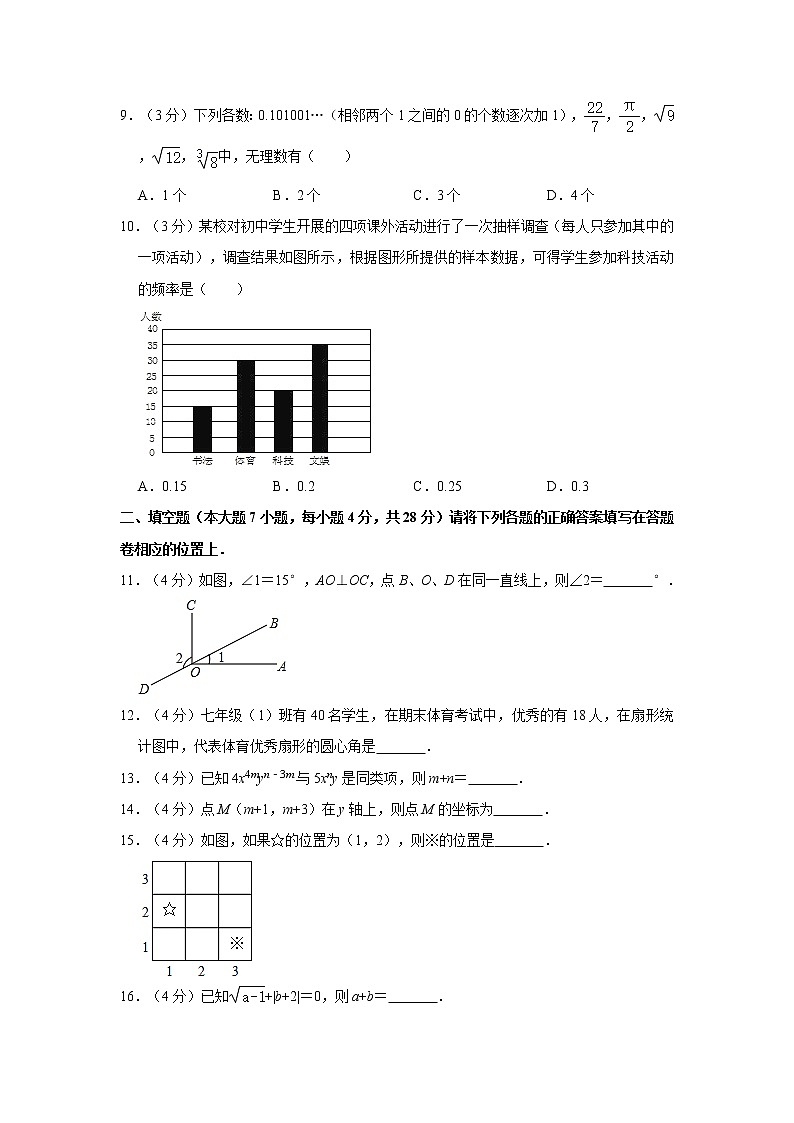
10.(3分)某校对初中学生开展的四项课外活动进行了一次抽样调查(每人只参加其中的一项活动),调查结果如图所示,根据图形所提供的样本数据,可得学生参加科技活动的频率是( )
A.0.15 B.0.2 C.0.25 D.0.3
二、填空题(本大题7小题,每小题4分,共28分)请将下列各题的正确答案填写在答题卷相应的位置上.
11.(4分)如图,∠1=15°,AO⊥OC,点B、O、D在同一直线上,则∠2= °.
12.(4分)七年级(1)班有40名学生,在期末体育考试中,优秀的有18人,在扇形统计图中,代表体育优秀扇形的圆心角是 .
13.(4分)已知4x4myn﹣3m与5xny是同类项,则m+n= .
14.(4分)点M(m+1,m+3)在y轴上,则点M的坐标为 .
15.(4分)如图,如果☆的位置为(1,2),则※的位置是 .
16.(4分)已知+|b+2|=0,则a+b= .
17.(4分)若点P(2x,x﹣3)到两坐标轴的距离之和为5,则x的值为 .
三、解答题(一)(本大题3小题,每小题6分,共18分.)请将下列各题的解题过程写在答题卷相应的位置上.
18.(6分)解方程组:
(1);
(2).
19.(6分)解不等式组:,并把它的解集在数轴上表示出来.
20.(6分)如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0),C(2,2),将△ABC向左平移1个单位后再向下平移2单位,可得到△A′B′C′.
(1)请画出平移后的△A′B′C′的图形;
(2)写出△A′B′C′各个顶点的坐标;
(3)求△ABC的面积.
四、解答题(二)(本大题3小题,每小题8分,共24分.)请将下列各题的解题过程写在答题卷相应的位置上.
21.(8分)如果一个正数的平方根为a+1和a﹣5.
(1)求a和x的值;
(2)求7x+1的立方根.
22.(8分)如图,已知AD交BE于F,C在AB的延长线上,∠A=∠ADE.
(1)若∠EDC=3∠C,求∠C的度数;
(2)若∠C=∠E.求证:BE∥CD.
23.(8分)某市第三中学组织学生参加生命安全知识网络测试.小明对九年级2班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图.根据图表中的信息解答下列问题:
组别
分数段(x)
频数
A
0≤x<60
2
B
60≤x<70
5
C
70≤x<80
17
D
80≤x<90
a
E
90≤x≤100
b
(1)求九年级2班学生的人数;
(2)写出频数分布表中a,b的值;
(3)已知该市共有80000名中学生参加这次安全知识测试,若规定80分以上为优秀,估计该市本次测试成绩达到优秀的人数;
(4)小明通过该市教育网站搜索发现,全市参加本次测试的中学生中,成绩达到优秀有56320人.请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因.
五、解答题(三)(本大题2小题,每小题10分,共20分.)请将下列各题的解题过程写在答题卷相应的位置上.
24.(10分)某公司有A、B两种型号的客车共20辆,它们的载客量、每天的租金如表所示.已知在20辆客车都坐满的情况下,共载客720人.
A型号客车
B型号客车
载客量(人/辆)
45
30
租金(元/辆)
600
450
(1)求A、B两种型号的客车各有多少辆?
(2)某中学计划租用A、B两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元.
①求最多能租用多少辆A型号客车?
②若七年级的师生共有305人,请写出所有可能的租车方案,并确定最省钱的租车方案.
25.(10分)如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)∠CBD=
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.
2019-2020学年广东省云浮市郁南县七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本大题10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的,把你认为正确选项前的字母写在答题卷对应的位置上.
1.(3分)将如图所示的图案通过平移后可以得到的图案是( )
A. B. C. D.
【分析】根据平移只改变图形的位置,不改变图形的形状与大小解答.
【解答】解:观察各选项图形可知,A选项的图案可以通过平移得到.
故选:A.
2.(3分)9的算术平方根是( )
A.3 B. C.9 D.±3
【分析】根据算术平方根的定义进行选择即可.
【解答】解:9的算术平方根是3,
故选:A.
3.(3分)如图,直线a,b被直线c所截,a∥b,∠1=60°,则∠2的度数是( )
A.120° B.60° C.45° D.30°
【分析】利用两直线平行,同位角相等就可求出.
【解答】解:∵直线被直线a、b被直线c所截,且a∥b,∠1=60°
∴∠2=∠1=60°.
故选:B.
4.(3分)在下列所给出坐标的点中,在第二象限的是( )
A.(2,3) B.(﹣2,3) C.(﹣2,﹣3) D.(2,﹣3)
【分析】根据第二象限内点的坐标符号(﹣,+)进行判断即可.
【解答】解:根据每个象限内点的坐标符号可得在第二象限内的点是(﹣2,3),
故选:B.
5.(3分)不等式2x>3﹣x的解集是( )
A.x>3 B.x<3 C.x>1 D.x<1
【分析】由一元一次不等式的解法知:解此不等式只需移项,系数化1两步即可得解集.
【解答】解:不等式2x>3﹣x移项得,
2x+x>3,
即3x>3,
系数化1得;
x>1.
故选:C.
6.(3分)已知是方程kx+y=3的一个解,那么k的值是( )
A.2 B.﹣2 C.1 D.﹣1
【分析】把代入方程kx+y=3得到关于k的一元一次方程,解之即可.
【解答】解:把代入方程kx+y=3得:
2k+1=3,
解得:k=1,
故选:C.
7.(3分)若a>b,则下列不等式正确的是( )
A.a﹣b<0 B.a+8<b﹣8 C.﹣5a<﹣5b D.
【分析】不等式加或减某个数或式子,乘或除以同一个正数,不等号的方向不变;乘或除以一个负数,不等号的方向改变.
【解答】解:A、不等式两边同时减去b,不等号的方向不变,故本选项错误;
B、不等式的两边应该加(或减去)同一个数8,不等号是方向才会不改变;故本选项错误;
C、不等式两边都乘以﹣5,不等号的方向改变,故本选项正确;
D、不等式两边都除以4,不等号的方向不变,故本选项错误;
故选:C.
8.(3分)用加减消元法解二元一次方程组,由①﹣②可得的方程为( )
A.3x=5 B.﹣3x=9 C.﹣3x﹣6y=9 D.3x﹣6y=5
【分析】利用加减消元法判断即可.
【解答】解:用加减消元法解二元一次方程组,由①﹣②可得的方程为﹣3x=9,
故选:B.
9.(3分)下列各数:0.101001…(相邻两个1之间的0的个数逐次加1),,,,,中,无理数有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据无理数的定义逐个判断即可.
【解答】解:无理数有:0.101001…(相邻两个1之间的0的个数逐次加1),,,共3个,
故选:C.
10.(3分)某校对初中学生开展的四项课外活动进行了一次抽样调查(每人只参加其中的一项活动),调查结果如图所示,根据图形所提供的样本数据,可得学生参加科技活动的频率是( )
A.0.15 B.0.2 C.0.25 D.0.3
【分析】首先根据统计图,得到总人数和参加科技活动的人数;
再根据频率=频数÷总数进行计算.
【解答】解:读图可知:共有(15+30+20+35)=100人,参加科技活动的频数是20.
故参加科技活动的频率0.2.
故选:B.
二、填空题(本大题7小题,每小题4分,共28分)请将下列各题的正确答案填写在答题卷相应的位置上.
11.(4分)如图,∠1=15°,AO⊥OC,点B、O、D在同一直线上,则∠2= 105 °.
【分析】由OA⊥OC可得∠AOC=90°,易得∠BOC,再由邻补角的定义可得∠2.
【解答】解:∵OA⊥OC,
∴∠AOC=90°,
∴∠BOC=90°﹣∠1=90°﹣15°=75°,
∴∠2=180°﹣∠BOC=180°﹣75°=105°,
故答案为:105.
12.(4分)七年级(1)班有40名学生,在期末体育考试中,优秀的有18人,在扇形统计图中,代表体育优秀扇形的圆心角是 162° .
【分析】先求出体育优秀的占总体的百分比,再乘以360°即可.
【解答】解:在扇形统计图中,代表体育优秀扇形的圆心角是360°×=162°,
故答案为:162°.
13.(4分)已知4x4myn﹣3m与5xny是同类项,则m+n= 5 .
【分析】根据同类项的定义(所含字母相同,相同字母的指数相同)列出方程求出n,m的值,再代入代数式计算即可.
【解答】解:根据题意得:,
解得:,
则m+n=1+4=5.
故答案是:5.
14.(4分)点M(m+1,m+3)在y轴上,则点M的坐标为 (0,2) .
【分析】直接利用y轴上点的坐标特点得出m的值,进而得出答案.
【解答】解:∵点M(m+1,m+3)在y轴上,
∴m+1=0,
解得:m=﹣1,
故m+3=2,
则点M的坐标为:(0,2).
故答案为:(0,2).
15.(4分)如图,如果☆的位置为(1,2),则※的位置是 (3,1) .
【分析】数对表示位置的方法是:第一个数字表示列,第二个数字表示行,由此即可解答问题.
【解答】解:☆的位置是(1,2 ),是第1列第2行;※位于第3列第1行,用数对表示为( 3,1).
故答案为:(3,1).
16.(4分)已知+|b+2|=0,则a+b= ﹣1 .
【分析】直接利用非负数的性质得出a,b的值,进而得出答案.
【解答】解:∵+|b+2|=0,
∴a=1,b=﹣2,
∴a+b=1﹣2=﹣1.
故答案为:﹣1.
17.(4分)若点P(2x,x﹣3)到两坐标轴的距离之和为5,则x的值为 x=﹣或x=2 .
【分析】分别利用P点在第一、二、三、四象限以及在坐标轴上分别分析得出答案.
【解答】解:当点P在第一象限,x﹣3>0,
解得:x>3,
且2x+x﹣3=5,
解得:x=<3,不合题意;
当点P在第二象限,,
不等式组无解,不合题意;
当点P在第三象限,
,
不等式组的解集为:x<0,
则﹣2x﹣x+3=5,
解得:x=﹣;
当点P在第四象限,
则,
不等式组的解集为:0<x<3,
故2x﹣(x﹣3)=5,
解得:x=2,
当点P在x轴上,则x﹣3=0,
解得:x=3,此时2x=6,不合题意;
当点P在y轴上,则2x=0,
解得:x=0,此时|x﹣3|=3,不合题意;
综上所述:x=﹣或x=2.
三、解答题(一)(本大题3小题,每小题6分,共18分.)请将下列各题的解题过程写在答题卷相应的位置上.
18.(6分)解方程组:
(1);
(2).
【分析】(1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
【解答】解:(1),
把②代入①得:10+6y+3y=1,
解得:y=﹣1,
把y=﹣1代入②得:x=2,
则方程组的解为;
(2),
①×2+②×3得:13x=38,
解得:x=,
把x=代入①得:y=﹣,
则方程组的解为.
19.(6分)解不等式组:,并把它的解集在数轴上表示出来.
【分析】先求出不等式组中的每一个不等式的解集,然后取其交集即为不等式组的解集;最后根据在数轴上表示不等式的解集的方法将其表示在数轴上.
【解答】解:由原不等式组,得,
即,
所以不等式组的解集是:﹣1<x≤2;
把不等式组的解集,在数轴上表示如图:
20.(6分)如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0),C(2,2),将△ABC向左平移1个单位后再向下平移2单位,可得到△A′B′C′.
(1)请画出平移后的△A′B′C′的图形;
(2)写出△A′B′C′各个顶点的坐标;
(3)求△ABC的面积.
【分析】(1)根据网格结构找出点A、B、C平移后的对应点A′、B′、C′的位置,然后顺次连接即可;
(2)根据平面直角坐标系写出各点的坐标即可;
(3)根据图形得到△ABC的底边AB和AB边上的高,利用三角形的面积公式列式计算即可得解.
【解答】解:(1)△A′B′C′如图所示;
(2)A′(﹣1,﹣2),B′(2,﹣2),C′(1,0);
(3)S△ABC=×3×2=3.
四、解答题(二)(本大题3小题,每小题8分,共24分.)请将下列各题的解题过程写在答题卷相应的位置上.
21.(8分)如果一个正数的平方根为a+1和a﹣5.
(1)求a和x的值;
(2)求7x+1的立方根.
【分析】(1)由于一个正数的平方根有两个,它们互为相反数,由此即可得到关于a的方程,解方程即可解决问题;
(2)先计算出7x+1的值,再根据立方根的定义,即可解答.
【解答】解:(1)∵一个正数的平方根为a+1和a﹣5.
∴a+1+a﹣5=0,
解得:a=2,
a+1=3,
∴x=32=9.
(2)7x+1=7×9+1=64,64的立方根为4.
22.(8分)如图,已知AD交BE于F,C在AB的延长线上,∠A=∠ADE.
(1)若∠EDC=3∠C,求∠C的度数;
(2)若∠C=∠E.求证:BE∥CD.
【分析】(1)根据两直线平行,同旁内角互补,即可得出∠C的度数;
(2)根据AC∥DE,∠C=∠E,即可得出∠C=∠ABE,进而判定BE∥CD.
【解答】解:(1)∵∠A=∠ADE,
∴AC∥DE,
∴∠EDC+∠C=180°,
又∵∠EDC=3∠C,
∴4∠C=180°,
即∠C=45°;
(2)∵AC∥DE,
∴∠E=∠ABE,
又∵∠C=∠E,
∴∠C=∠ABE,
∴BE∥CD.
23.(8分)某市第三中学组织学生参加生命安全知识网络测试.小明对九年级2班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图.根据图表中的信息解答下列问题:
组别
分数段(x)
频数
A
0≤x<60
2
B
60≤x<70
5
C
70≤x<80
17
D
80≤x<90
a
E
90≤x≤100
b
(1)求九年级2班学生的人数;
(2)写出频数分布表中a,b的值;
(3)已知该市共有80000名中学生参加这次安全知识测试,若规定80分以上为优秀,估计该市本次测试成绩达到优秀的人数;
(4)小明通过该市教育网站搜索发现,全市参加本次测试的中学生中,成绩达到优秀有56320人.请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因.
【分析】(1)根据数据总数=代入计算,求出九年级2班学生的人数;
(2)a是D组的频数=百分比×总数;b是E组的频数=50﹣各组频数;
(3)先计算优秀的百分比,再与80000相乘即可;
(4)取的样本不足以代表全市总中学的总体情况.
【解答】解:(1)17÷34%=50(人),
答:九年级2班学生的人数为50人;
(2)a=24%×50=12,
b=50﹣2﹣5﹣17﹣12=14,
(3)E:14÷50=28%,
(28%+24%)×80000=52×800=41600(人),
答:估计该市本次测试成绩达到优秀的人数为41600人;
(4)全市参加本次测试的中学生中,成绩达到优秀有56 320人;而样本中估计该市本次测试成绩达到优秀的人数为41600人,原因是:小明对第三中学九年2班全体学生的测试成绩取的样本不足以代表全市总中学的总体情况,所以会出现较大偏差.
五、解答题(三)(本大题2小题,每小题10分,共20分.)请将下列各题的解题过程写在答题卷相应的位置上.
24.(10分)某公司有A、B两种型号的客车共20辆,它们的载客量、每天的租金如表所示.已知在20辆客车都坐满的情况下,共载客720人.
A型号客车
B型号客车
载客量(人/辆)
45
30
租金(元/辆)
600
450
(1)求A、B两种型号的客车各有多少辆?
(2)某中学计划租用A、B两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元.
①求最多能租用多少辆A型号客车?
②若七年级的师生共有305人,请写出所有可能的租车方案,并确定最省钱的租车方案.
【分析】(1)设A型号的客车有x辆,B型号的客车有y辆,由题意得等量关系:①A、B两种型号的客车共20辆;②共载客720人,根据等量关系列出方程组,再解即可;
(2)①设租用A型号的客车m辆,则租用B型号客车(8﹣m)辆,由题意得不等关系:A的总租金+B的总租金≤4600,根据不等关系列出不等式,再解即可;
②根据题意可得不等关系:A的总载客人数+B的总载客人数≥305,根据不等关系,列出不等式,再解可得m的范围,再结合①中m的范围,确定m的值.
【解答】解:(1)设A型号的客车有x辆,B型号的客车有y辆,由题意得:
,
解得:,
答:A型号的客车有8辆,B型号的客车有12辆.
(2)①设租用A型号的客车m辆,则租用B型号客车(8﹣m)辆,由题意得:
600m+450(8﹣m)≤4600,
解得:m≤,
答:最多能租用6辆A型号客车;
②由题意得:45m+30(8﹣m)≥305,
解得:m≥,
由①知,m≤,
则<m≤,
∵m为非负整数,
∴m=5,6,
∴方案1,租用5辆A型号客车,租用3辆B型号客车;
方案2,租用6辆A型号客车,租用2辆B型号客车;
∵B型号租金少,
∴多租B,少租A,
因此租用5辆A型号客车,租用3辆B型号客车最省钱.
25.(10分)如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)∠CBD= 60°
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC= 30°
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.
【分析】(1)根据角平分线的定义只要证明∠CBD=∠ABN即可;
(2)想办法证明∠ABC=∠CBP=∠DBP=∠DBN即可解决问题;
(3)不变.可以证明∠APB=∠PBN,∠ADB=∠DBN=∠PBN.
【解答】解:(1)∵AM∥BN,
∴∠ABN=180°﹣∠A=120°,
又∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBD=∠CBP+∠DBP=(∠ABP+∠PBN)=∠ABN=60°,
故答案为:60°.
(2)∵AM∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠ABD﹣∠CBD=∠CBN﹣∠CBD=∠DBN,
∴∠ABC=∠CBP=∠DBP=∠DBN,
∴∠ABC=∠ABN=30°,
故答案为:30°.
(3)不变.理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠ADB=∠DBN=∠PBN=∠APB,即∠APB:∠ADB=2:1.
一、选择题(本大题10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的,把你认为正确选项前的字母写在答题卷对应的位置上.
1.(3分)将如图所示的图案通过平移后可以得到的图案是( )
A. B. C. D.
2.(3分)9的算术平方根是( )
A.3 B. C.9 D.±3
3.(3分)如图,直线a,b被直线c所截,a∥b,∠1=60°,则∠2的度数是( )
A.120° B.60° C.45° D.30°
4.(3分)在下列所给出坐标的点中,在第二象限的是( )
A.(2,3) B.(﹣2,3) C.(﹣2,﹣3) D.(2,﹣3)
5.(3分)不等式2x>3﹣x的解集是( )
A.x>3 B.x<3 C.x>1 D.x<1
6.(3分)已知是方程kx+y=3的一个解,那么k的值是( )
A.2 B.﹣2 C.1 D.﹣1
7.(3分)若a>b,则下列不等式正确的是( )
A.a﹣b<0 B.a+8<b﹣8 C.﹣5a<﹣5b D.
8.(3分)用加减消元法解二元一次方程组,由①﹣②可得的方程为( )
A.3x=5 B.﹣3x=9 C.﹣3x﹣6y=9 D.3x﹣6y=5
9.(3分)下列各数:0.101001…(相邻两个1之间的0的个数逐次加1),,,,,中,无理数有( )
A.1个 B.2个 C.3个 D.4个
10.(3分)某校对初中学生开展的四项课外活动进行了一次抽样调查(每人只参加其中的一项活动),调查结果如图所示,根据图形所提供的样本数据,可得学生参加科技活动的频率是( )
A.0.15 B.0.2 C.0.25 D.0.3
二、填空题(本大题7小题,每小题4分,共28分)请将下列各题的正确答案填写在答题卷相应的位置上.
11.(4分)如图,∠1=15°,AO⊥OC,点B、O、D在同一直线上,则∠2= °.
12.(4分)七年级(1)班有40名学生,在期末体育考试中,优秀的有18人,在扇形统计图中,代表体育优秀扇形的圆心角是 .
13.(4分)已知4x4myn﹣3m与5xny是同类项,则m+n= .
14.(4分)点M(m+1,m+3)在y轴上,则点M的坐标为 .
15.(4分)如图,如果☆的位置为(1,2),则※的位置是 .
16.(4分)已知+|b+2|=0,则a+b= .
17.(4分)若点P(2x,x﹣3)到两坐标轴的距离之和为5,则x的值为 .
三、解答题(一)(本大题3小题,每小题6分,共18分.)请将下列各题的解题过程写在答题卷相应的位置上.
18.(6分)解方程组:
(1);
(2).
19.(6分)解不等式组:,并把它的解集在数轴上表示出来.
20.(6分)如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0),C(2,2),将△ABC向左平移1个单位后再向下平移2单位,可得到△A′B′C′.
(1)请画出平移后的△A′B′C′的图形;
(2)写出△A′B′C′各个顶点的坐标;
(3)求△ABC的面积.
四、解答题(二)(本大题3小题,每小题8分,共24分.)请将下列各题的解题过程写在答题卷相应的位置上.
21.(8分)如果一个正数的平方根为a+1和a﹣5.
(1)求a和x的值;
(2)求7x+1的立方根.
22.(8分)如图,已知AD交BE于F,C在AB的延长线上,∠A=∠ADE.
(1)若∠EDC=3∠C,求∠C的度数;
(2)若∠C=∠E.求证:BE∥CD.
23.(8分)某市第三中学组织学生参加生命安全知识网络测试.小明对九年级2班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图.根据图表中的信息解答下列问题:
组别
分数段(x)
频数
A
0≤x<60
2
B
60≤x<70
5
C
70≤x<80
17
D
80≤x<90
a
E
90≤x≤100
b
(1)求九年级2班学生的人数;
(2)写出频数分布表中a,b的值;
(3)已知该市共有80000名中学生参加这次安全知识测试,若规定80分以上为优秀,估计该市本次测试成绩达到优秀的人数;
(4)小明通过该市教育网站搜索发现,全市参加本次测试的中学生中,成绩达到优秀有56320人.请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因.
五、解答题(三)(本大题2小题,每小题10分,共20分.)请将下列各题的解题过程写在答题卷相应的位置上.
24.(10分)某公司有A、B两种型号的客车共20辆,它们的载客量、每天的租金如表所示.已知在20辆客车都坐满的情况下,共载客720人.
A型号客车
B型号客车
载客量(人/辆)
45
30
租金(元/辆)
600
450
(1)求A、B两种型号的客车各有多少辆?
(2)某中学计划租用A、B两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元.
①求最多能租用多少辆A型号客车?
②若七年级的师生共有305人,请写出所有可能的租车方案,并确定最省钱的租车方案.
25.(10分)如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)∠CBD=
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.
2019-2020学年广东省云浮市郁南县七年级(下)期末数学试卷
参考答案与试题解析
一、选择题(本大题10小题,每小题3分,共30分)在每小题列出的四个选项中,只有一个是正确的,把你认为正确选项前的字母写在答题卷对应的位置上.
1.(3分)将如图所示的图案通过平移后可以得到的图案是( )
A. B. C. D.
【分析】根据平移只改变图形的位置,不改变图形的形状与大小解答.
【解答】解:观察各选项图形可知,A选项的图案可以通过平移得到.
故选:A.
2.(3分)9的算术平方根是( )
A.3 B. C.9 D.±3
【分析】根据算术平方根的定义进行选择即可.
【解答】解:9的算术平方根是3,
故选:A.
3.(3分)如图,直线a,b被直线c所截,a∥b,∠1=60°,则∠2的度数是( )
A.120° B.60° C.45° D.30°
【分析】利用两直线平行,同位角相等就可求出.
【解答】解:∵直线被直线a、b被直线c所截,且a∥b,∠1=60°
∴∠2=∠1=60°.
故选:B.
4.(3分)在下列所给出坐标的点中,在第二象限的是( )
A.(2,3) B.(﹣2,3) C.(﹣2,﹣3) D.(2,﹣3)
【分析】根据第二象限内点的坐标符号(﹣,+)进行判断即可.
【解答】解:根据每个象限内点的坐标符号可得在第二象限内的点是(﹣2,3),
故选:B.
5.(3分)不等式2x>3﹣x的解集是( )
A.x>3 B.x<3 C.x>1 D.x<1
【分析】由一元一次不等式的解法知:解此不等式只需移项,系数化1两步即可得解集.
【解答】解:不等式2x>3﹣x移项得,
2x+x>3,
即3x>3,
系数化1得;
x>1.
故选:C.
6.(3分)已知是方程kx+y=3的一个解,那么k的值是( )
A.2 B.﹣2 C.1 D.﹣1
【分析】把代入方程kx+y=3得到关于k的一元一次方程,解之即可.
【解答】解:把代入方程kx+y=3得:
2k+1=3,
解得:k=1,
故选:C.
7.(3分)若a>b,则下列不等式正确的是( )
A.a﹣b<0 B.a+8<b﹣8 C.﹣5a<﹣5b D.
【分析】不等式加或减某个数或式子,乘或除以同一个正数,不等号的方向不变;乘或除以一个负数,不等号的方向改变.
【解答】解:A、不等式两边同时减去b,不等号的方向不变,故本选项错误;
B、不等式的两边应该加(或减去)同一个数8,不等号是方向才会不改变;故本选项错误;
C、不等式两边都乘以﹣5,不等号的方向改变,故本选项正确;
D、不等式两边都除以4,不等号的方向不变,故本选项错误;
故选:C.
8.(3分)用加减消元法解二元一次方程组,由①﹣②可得的方程为( )
A.3x=5 B.﹣3x=9 C.﹣3x﹣6y=9 D.3x﹣6y=5
【分析】利用加减消元法判断即可.
【解答】解:用加减消元法解二元一次方程组,由①﹣②可得的方程为﹣3x=9,
故选:B.
9.(3分)下列各数:0.101001…(相邻两个1之间的0的个数逐次加1),,,,,中,无理数有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据无理数的定义逐个判断即可.
【解答】解:无理数有:0.101001…(相邻两个1之间的0的个数逐次加1),,,共3个,
故选:C.
10.(3分)某校对初中学生开展的四项课外活动进行了一次抽样调查(每人只参加其中的一项活动),调查结果如图所示,根据图形所提供的样本数据,可得学生参加科技活动的频率是( )
A.0.15 B.0.2 C.0.25 D.0.3
【分析】首先根据统计图,得到总人数和参加科技活动的人数;
再根据频率=频数÷总数进行计算.
【解答】解:读图可知:共有(15+30+20+35)=100人,参加科技活动的频数是20.
故参加科技活动的频率0.2.
故选:B.
二、填空题(本大题7小题,每小题4分,共28分)请将下列各题的正确答案填写在答题卷相应的位置上.
11.(4分)如图,∠1=15°,AO⊥OC,点B、O、D在同一直线上,则∠2= 105 °.
【分析】由OA⊥OC可得∠AOC=90°,易得∠BOC,再由邻补角的定义可得∠2.
【解答】解:∵OA⊥OC,
∴∠AOC=90°,
∴∠BOC=90°﹣∠1=90°﹣15°=75°,
∴∠2=180°﹣∠BOC=180°﹣75°=105°,
故答案为:105.
12.(4分)七年级(1)班有40名学生,在期末体育考试中,优秀的有18人,在扇形统计图中,代表体育优秀扇形的圆心角是 162° .
【分析】先求出体育优秀的占总体的百分比,再乘以360°即可.
【解答】解:在扇形统计图中,代表体育优秀扇形的圆心角是360°×=162°,
故答案为:162°.
13.(4分)已知4x4myn﹣3m与5xny是同类项,则m+n= 5 .
【分析】根据同类项的定义(所含字母相同,相同字母的指数相同)列出方程求出n,m的值,再代入代数式计算即可.
【解答】解:根据题意得:,
解得:,
则m+n=1+4=5.
故答案是:5.
14.(4分)点M(m+1,m+3)在y轴上,则点M的坐标为 (0,2) .
【分析】直接利用y轴上点的坐标特点得出m的值,进而得出答案.
【解答】解:∵点M(m+1,m+3)在y轴上,
∴m+1=0,
解得:m=﹣1,
故m+3=2,
则点M的坐标为:(0,2).
故答案为:(0,2).
15.(4分)如图,如果☆的位置为(1,2),则※的位置是 (3,1) .
【分析】数对表示位置的方法是:第一个数字表示列,第二个数字表示行,由此即可解答问题.
【解答】解:☆的位置是(1,2 ),是第1列第2行;※位于第3列第1行,用数对表示为( 3,1).
故答案为:(3,1).
16.(4分)已知+|b+2|=0,则a+b= ﹣1 .
【分析】直接利用非负数的性质得出a,b的值,进而得出答案.
【解答】解:∵+|b+2|=0,
∴a=1,b=﹣2,
∴a+b=1﹣2=﹣1.
故答案为:﹣1.
17.(4分)若点P(2x,x﹣3)到两坐标轴的距离之和为5,则x的值为 x=﹣或x=2 .
【分析】分别利用P点在第一、二、三、四象限以及在坐标轴上分别分析得出答案.
【解答】解:当点P在第一象限,x﹣3>0,
解得:x>3,
且2x+x﹣3=5,
解得:x=<3,不合题意;
当点P在第二象限,,
不等式组无解,不合题意;
当点P在第三象限,
,
不等式组的解集为:x<0,
则﹣2x﹣x+3=5,
解得:x=﹣;
当点P在第四象限,
则,
不等式组的解集为:0<x<3,
故2x﹣(x﹣3)=5,
解得:x=2,
当点P在x轴上,则x﹣3=0,
解得:x=3,此时2x=6,不合题意;
当点P在y轴上,则2x=0,
解得:x=0,此时|x﹣3|=3,不合题意;
综上所述:x=﹣或x=2.
三、解答题(一)(本大题3小题,每小题6分,共18分.)请将下列各题的解题过程写在答题卷相应的位置上.
18.(6分)解方程组:
(1);
(2).
【分析】(1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
【解答】解:(1),
把②代入①得:10+6y+3y=1,
解得:y=﹣1,
把y=﹣1代入②得:x=2,
则方程组的解为;
(2),
①×2+②×3得:13x=38,
解得:x=,
把x=代入①得:y=﹣,
则方程组的解为.
19.(6分)解不等式组:,并把它的解集在数轴上表示出来.
【分析】先求出不等式组中的每一个不等式的解集,然后取其交集即为不等式组的解集;最后根据在数轴上表示不等式的解集的方法将其表示在数轴上.
【解答】解:由原不等式组,得,
即,
所以不等式组的解集是:﹣1<x≤2;
把不等式组的解集,在数轴上表示如图:
20.(6分)如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0),C(2,2),将△ABC向左平移1个单位后再向下平移2单位,可得到△A′B′C′.
(1)请画出平移后的△A′B′C′的图形;
(2)写出△A′B′C′各个顶点的坐标;
(3)求△ABC的面积.
【分析】(1)根据网格结构找出点A、B、C平移后的对应点A′、B′、C′的位置,然后顺次连接即可;
(2)根据平面直角坐标系写出各点的坐标即可;
(3)根据图形得到△ABC的底边AB和AB边上的高,利用三角形的面积公式列式计算即可得解.
【解答】解:(1)△A′B′C′如图所示;
(2)A′(﹣1,﹣2),B′(2,﹣2),C′(1,0);
(3)S△ABC=×3×2=3.
四、解答题(二)(本大题3小题,每小题8分,共24分.)请将下列各题的解题过程写在答题卷相应的位置上.
21.(8分)如果一个正数的平方根为a+1和a﹣5.
(1)求a和x的值;
(2)求7x+1的立方根.
【分析】(1)由于一个正数的平方根有两个,它们互为相反数,由此即可得到关于a的方程,解方程即可解决问题;
(2)先计算出7x+1的值,再根据立方根的定义,即可解答.
【解答】解:(1)∵一个正数的平方根为a+1和a﹣5.
∴a+1+a﹣5=0,
解得:a=2,
a+1=3,
∴x=32=9.
(2)7x+1=7×9+1=64,64的立方根为4.
22.(8分)如图,已知AD交BE于F,C在AB的延长线上,∠A=∠ADE.
(1)若∠EDC=3∠C,求∠C的度数;
(2)若∠C=∠E.求证:BE∥CD.
【分析】(1)根据两直线平行,同旁内角互补,即可得出∠C的度数;
(2)根据AC∥DE,∠C=∠E,即可得出∠C=∠ABE,进而判定BE∥CD.
【解答】解:(1)∵∠A=∠ADE,
∴AC∥DE,
∴∠EDC+∠C=180°,
又∵∠EDC=3∠C,
∴4∠C=180°,
即∠C=45°;
(2)∵AC∥DE,
∴∠E=∠ABE,
又∵∠C=∠E,
∴∠C=∠ABE,
∴BE∥CD.
23.(8分)某市第三中学组织学生参加生命安全知识网络测试.小明对九年级2班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图.根据图表中的信息解答下列问题:
组别
分数段(x)
频数
A
0≤x<60
2
B
60≤x<70
5
C
70≤x<80
17
D
80≤x<90
a
E
90≤x≤100
b
(1)求九年级2班学生的人数;
(2)写出频数分布表中a,b的值;
(3)已知该市共有80000名中学生参加这次安全知识测试,若规定80分以上为优秀,估计该市本次测试成绩达到优秀的人数;
(4)小明通过该市教育网站搜索发现,全市参加本次测试的中学生中,成绩达到优秀有56320人.请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因.
【分析】(1)根据数据总数=代入计算,求出九年级2班学生的人数;
(2)a是D组的频数=百分比×总数;b是E组的频数=50﹣各组频数;
(3)先计算优秀的百分比,再与80000相乘即可;
(4)取的样本不足以代表全市总中学的总体情况.
【解答】解:(1)17÷34%=50(人),
答:九年级2班学生的人数为50人;
(2)a=24%×50=12,
b=50﹣2﹣5﹣17﹣12=14,
(3)E:14÷50=28%,
(28%+24%)×80000=52×800=41600(人),
答:估计该市本次测试成绩达到优秀的人数为41600人;
(4)全市参加本次测试的中学生中,成绩达到优秀有56 320人;而样本中估计该市本次测试成绩达到优秀的人数为41600人,原因是:小明对第三中学九年2班全体学生的测试成绩取的样本不足以代表全市总中学的总体情况,所以会出现较大偏差.
五、解答题(三)(本大题2小题,每小题10分,共20分.)请将下列各题的解题过程写在答题卷相应的位置上.
24.(10分)某公司有A、B两种型号的客车共20辆,它们的载客量、每天的租金如表所示.已知在20辆客车都坐满的情况下,共载客720人.
A型号客车
B型号客车
载客量(人/辆)
45
30
租金(元/辆)
600
450
(1)求A、B两种型号的客车各有多少辆?
(2)某中学计划租用A、B两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元.
①求最多能租用多少辆A型号客车?
②若七年级的师生共有305人,请写出所有可能的租车方案,并确定最省钱的租车方案.
【分析】(1)设A型号的客车有x辆,B型号的客车有y辆,由题意得等量关系:①A、B两种型号的客车共20辆;②共载客720人,根据等量关系列出方程组,再解即可;
(2)①设租用A型号的客车m辆,则租用B型号客车(8﹣m)辆,由题意得不等关系:A的总租金+B的总租金≤4600,根据不等关系列出不等式,再解即可;
②根据题意可得不等关系:A的总载客人数+B的总载客人数≥305,根据不等关系,列出不等式,再解可得m的范围,再结合①中m的范围,确定m的值.
【解答】解:(1)设A型号的客车有x辆,B型号的客车有y辆,由题意得:
,
解得:,
答:A型号的客车有8辆,B型号的客车有12辆.
(2)①设租用A型号的客车m辆,则租用B型号客车(8﹣m)辆,由题意得:
600m+450(8﹣m)≤4600,
解得:m≤,
答:最多能租用6辆A型号客车;
②由题意得:45m+30(8﹣m)≥305,
解得:m≥,
由①知,m≤,
则<m≤,
∵m为非负整数,
∴m=5,6,
∴方案1,租用5辆A型号客车,租用3辆B型号客车;
方案2,租用6辆A型号客车,租用2辆B型号客车;
∵B型号租金少,
∴多租B,少租A,
因此租用5辆A型号客车,租用3辆B型号客车最省钱.
25.(10分)如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)∠CBD= 60°
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC= 30°
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.
【分析】(1)根据角平分线的定义只要证明∠CBD=∠ABN即可;
(2)想办法证明∠ABC=∠CBP=∠DBP=∠DBN即可解决问题;
(3)不变.可以证明∠APB=∠PBN,∠ADB=∠DBN=∠PBN.
【解答】解:(1)∵AM∥BN,
∴∠ABN=180°﹣∠A=120°,
又∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBD=∠CBP+∠DBP=(∠ABP+∠PBN)=∠ABN=60°,
故答案为:60°.
(2)∵AM∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠ABD﹣∠CBD=∠CBN﹣∠CBD=∠DBN,
∴∠ABC=∠CBP=∠DBP=∠DBN,
∴∠ABC=∠ABN=30°,
故答案为:30°.
(3)不变.理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠ADB=∠DBN=∠PBN=∠APB,即∠APB:∠ADB=2:1.
相关资料
更多








