人教版八年级上册第十一章 三角形11.2 与三角形有关的角11.2.1 三角形的内角教课课件ppt

这是一份人教版八年级上册第十一章 三角形11.2 与三角形有关的角11.2.1 三角形的内角教课课件ppt，共19页。PPT课件主要包含了三角形的内角，学习目标，复习回顾，讲授新知，探究实验，证法一，证法二，证法三，证法四，课堂小结等内容，欢迎下载使用。
1、会阐述三角形内角和定理。2、会应用三角形内角和定理进行计算；(求三角形的角的度数)3、能通过动手实践去验证三角形的内角和定理。
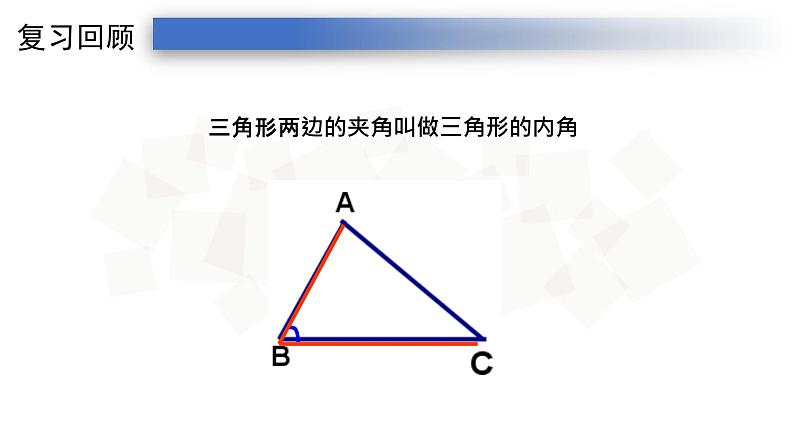
三角形两边的夹角叫做三角形的内角
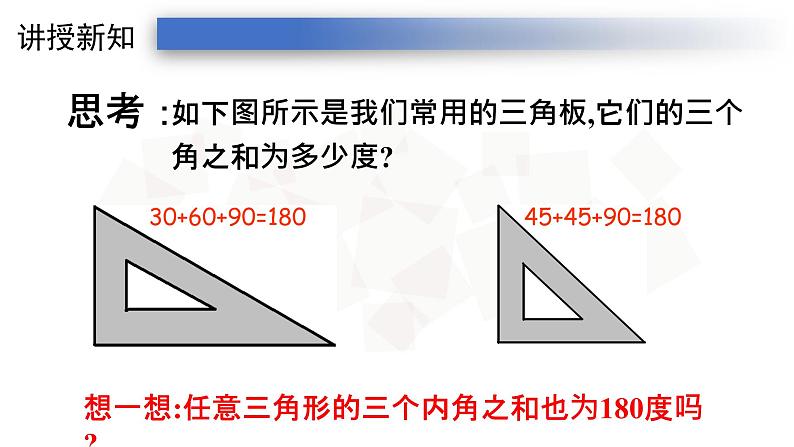
如下图所示是我们常用的三角板,它们的三个角之和为多少度?
想一想:任意三角形的三个内角之和也为180度吗?
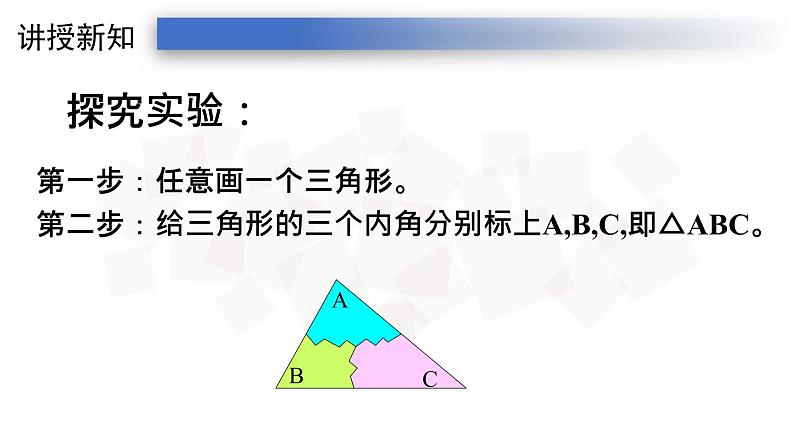
第二步：给三角形的三个内角分别标上A,B,C,即△ABC。
第一步：任意画一个三角形。
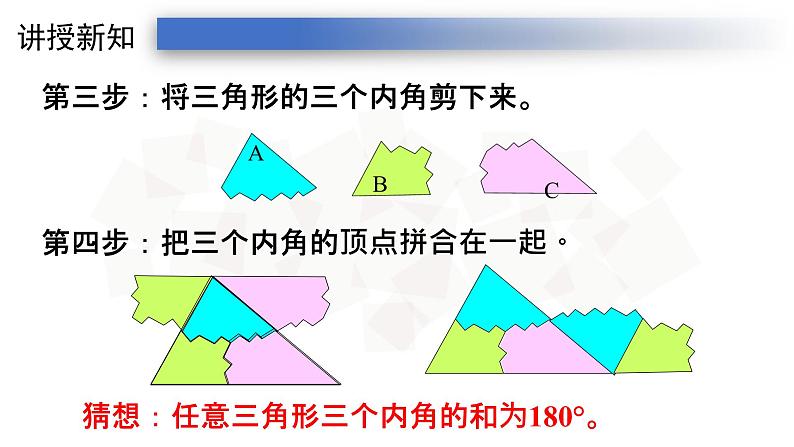
第四步：把三个内角的顶点拼合在一起。
第三步：将三角形的三个内角剪下来。
猜想：任意三角形三个内角的和为180°。
在实际证明过程中，为了证明的需要，往往需要在原来的图形上添画线条，这些线叫做辅助线。在平面几何里，辅助线通常画成虚线。
为了证明三个角的和为180°，转化为一个平角或同旁内角互补，这种转化思想是数学中的常用方法。
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
延长BC到D，过C作CE∥BA
(两直线平行，内错角相等)
(两直线平行，同位角相等)
∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
延长BC到D，在△ABC的外部，以CA为一边，CE为另一边作∠1=∠A
(内错角相等，两直线平行)
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
一、三角形的内角和任意三角形的三个内角之和为180度二、三角形内角和的证明1.辅助线2.转化法3.感受四种证明方法
1.下列各组角是同一个三角形的内角吗?为什么?
（2）60°， 40°， 90°
（3）30°， 60°， 50°
（1）3°， 150°， 27°
2.在△ABC中，∠A =500, ∠B =800,则∠C =（ ） A. 400 B. 500 C. 100 D. 11003.在△ABC中，∠A =800, ∠B =∠C，则∠B =（ ） A. 500 B. 400 C. 100 D. 450
4.如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是 ( )
(A)带①去　　　　 　　　 　　　 (B)带②去　　　(C)带③去　　　　　　　 　　　 　 (D)带①和②去
5.△ABC中,若∠A＋∠B＝∠C,则△ABC是( )A、锐角三角形 　 B、直角三角形 C、钝角三角形　 D、等腰三角形
6. 一个三角形至少有（ ） A、一个锐角 B、两个锐角 C、一个钝角 D、一个直角
7. 已知：在△ABC中，∠BAC=40°，∠B=75°，AD是△ABC的 角平分线 ， 求∠ADB的度数.
解:由∠BAC=40°， AD是△ABC的角平分线
∴ ∠BAD= ∠BAC=20°.
在△ABD中，∴ ∠ADB=180°-∠B-∠BAD =180°-75°-20°=85°.
5. 如图△ABC中,CD平分∠ACB,DE∥BC,∠A＝70°,∠ADE＝50°, 求∠BDC的度数.
∴∠ACB=180 °-∠A-∠B
=180°-70°-50°
∴∠B=∠ADE＝50°
∴∠DCB=1/2∠ACB=1/2x60°=30°
∴∠BDC=180°-∠B-∠DCB
=180°-50°-30°