北师大版3 正方形的性质与判定教案及反思

这是一份北师大版3 正方形的性质与判定教案及反思，共9页。

知识点精析：


知识点一：正方形的定义


有一组邻边相等，且有一个角是直角的平行四边形




















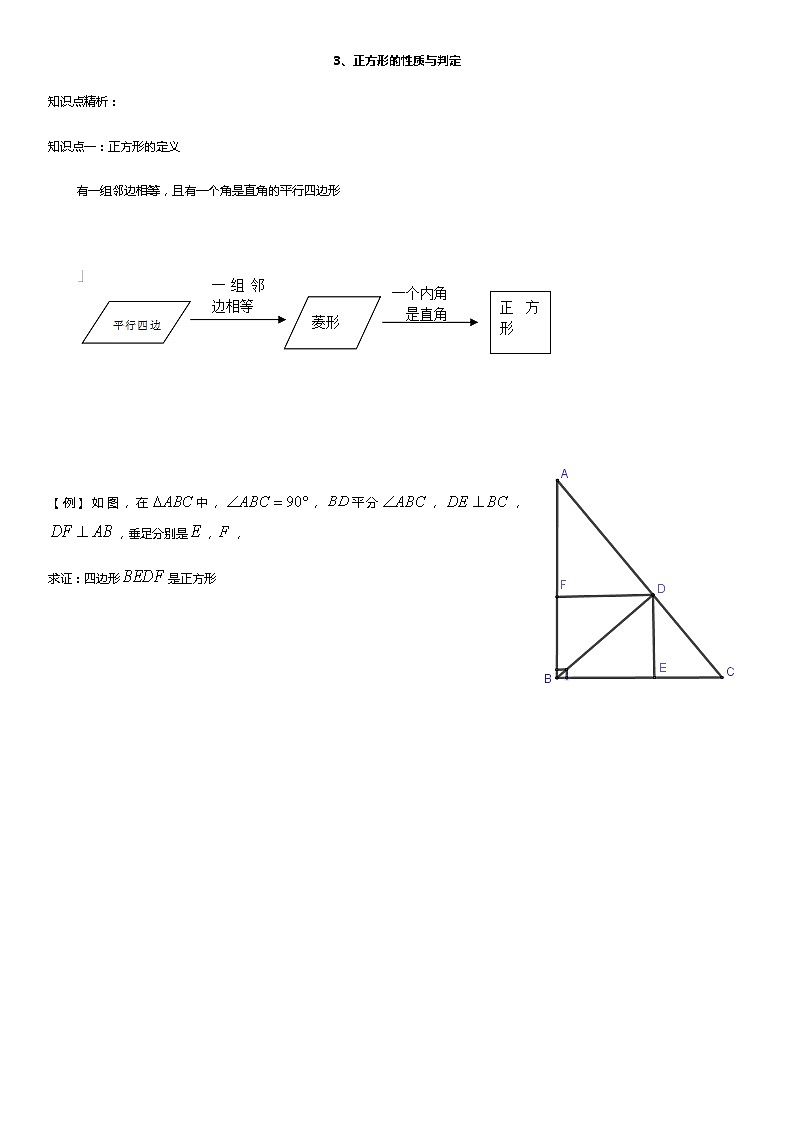
【例】如图，在中，，平分，，，垂足分别是，，


求证：四边形是正方形























知识点二：正方形的性质：（正方形具有平行四边形所有的性质）


边：四边相等


角：四个角都是直角


对角线：①对角线相互垂直；②对角线相等；③对角线平分每组对角（且平分后的角是）


对称性：正方形既是轴对称图形，也是中心对称图形








【例1】如图，正方形的边长为，为对角线，平分，，垂足为，求的长









































【例2】如图，在正方形中，对角线的交点为，是上一点，，垂足为点，交于点


求证：





知识点三：正方形的判定


判定：


（1）有一组邻边相等，且有一个角是直角的平行四边形是正方形（定义）


（2）对角线相等的菱形是正方形


（3）对角线相等的矩形是正方形


（4）有一个角是直角的菱形是正方形





【例1】如图，在中，，是的角平分线，点为的中点，连接，并延长到点，使，连接，


求证：四边形是矩形


当满足市民条件时，矩形是正方形？请说明理由


























【例2】已知在中，对角线，交于点，是的延长线上的点，且


求证：四边形是菱形


若，求证：四边形是正方形





知识点四：中点四边形（拓展）


【例】如图，在四边形中，，分别是，的中点，，分别是，的中点


当，满足什么条件时，四边形是矩形？


当，满足什么条件时，四边形是菱形？


当，满足什么条件时，四边形是正方形？
































知识点五：理由正方形的对称性求最值问题


【例1】如图，正方形的边长为，点在边上，且，点是边上一动点，则的最小值

















【例2】如图，正方形的边长为，为上的一点，，为上的一点，，为上一个动点，则的最小值是





课堂小练


基础巩固练


1、如图，在中，，的垂直平分线交于点，交于点，且，添加一个条件，仍不能证明四边形为正方形的是（）


BC=AC


CF⊥BF


BD=DF


AC=BF


2、如图，正方形的面积为1，则以相邻两边中点连线为边的正方形的周长为（）


A.


B.





C.


D.


3、如图，E，F分别是正方形的边，上的点，且,相交于点O，下列结论:


①；②AE⊥BF；③;④，其中正确的有（）


A.0个B.1个C.2个D.3个





4、如图，在正方形中，点为上一点，与交于点，若，则=








5、如图，正方形和正方形的边长分别是2和3，且点B，C，G在同一直线上，是线段的中点，连接，则=











6、如图，在正方形的外侧，作等边三角形，连接，


（1）求证：


（2）求∠BEC的度数














7、如图，在中，，，的平分线交于点，过作于点，于点,求证：四边形是正方形























8、如图，已知点是正方形的对角线上任一点，于，于，连接，；猜想线段与之间的关系并证明

















能力提升练


9、如图，在正方形中，△ABE和△CDF为直角三角形，∠AEB=∠CFD=90，AE=CF=5，BE=DF=12，则EF的长是（）


A.7


B.8


C.


D.


10、如图，正方形的边长为2，点E，F分别在边AD，CD上，若，


则的周长等于