初二数学上册秋季班培优讲义 第22讲 因式分解（五）

模块一：因式定理因式定理：如果时，多项式的值为0，那么是该多项式的一个因式．特别地，如果多项式的系数的和等于0，那么是多项式的一个因式；如果多项式的偶次项系数的和减去奇次项系数的和等于0，那么是多项式的一个因式．多项式性质：有理数的分子p是常数项的因数，分母q是首项系数的因数．例如：分解因式：．观察可知，当时，，则，其中A为整式，即是多项式的一个因式．若要确定整式A，则可用大除法．∴．模块二：待定系数法 如果两个多项式恒等，则左右两边同类项的系数相等．即，如果恒成立，那么，，…，，．待定系数法的使用前提是知道所需要求的代数式的形式，根据代数式的形式把不确定的部分设为未知数，然后通过比较系数得到方程，进而求解．
（1）观察可知，当__________时，．可得_________是多项式的一个因式．因式分解：________________． （2）观察可知，当_________时，．可得________是多项式的一个因式．因式分解：________________． （3）因式分解：．（1）当时，．可得是多项式的一个因式．因式分解：．（2）当时，．可得是多项式的一个因式．因式分解：．（3）原式有因式，原式．【教师备课提示】这道题主要让学生们熟悉因式定理的内容，而且是上讲拆项和添项的解释．因式分解：（1）      （2）（1）原式的有理数根只可能为：，，，，，，，，，，，，经检验使得原式为0，所以原式有因式，原式．（2）原式的有理根只能为：，，经检验使得原式=0，则原式必有因式，所以原式．【教师备课提示】这道题不像第一题一样了，各项的系数和没有特殊的关系，那就要用性质去试根，试出来一个根后再次用性质去试根，直到可以因式分解为止．
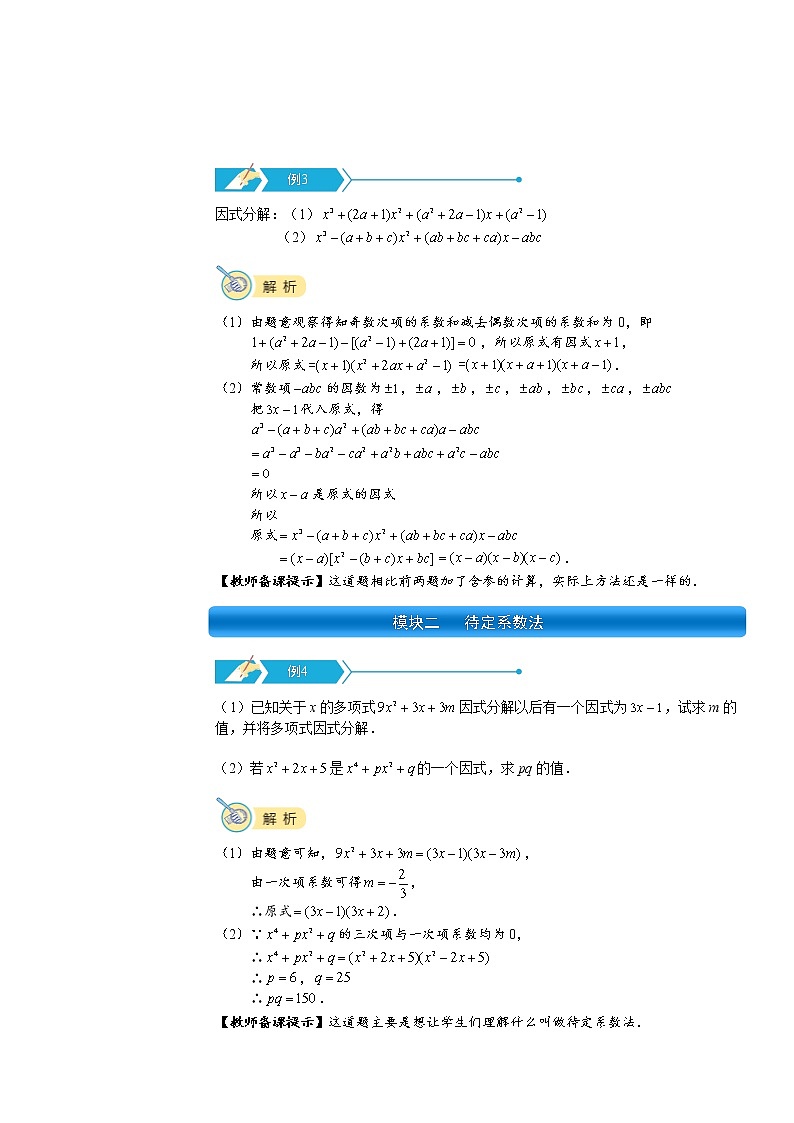
因式分解：（1）（2）（1）由题意观察得知奇数次项的系数和减去偶数次项的系数和为0，即，所以原式有因式，所以原式．（2）常数项的因数为，，，，，，，把代入原式，得 所以是原式的因式所以原式．【教师备课提示】这道题相比前两题加了含参的计算，实际上方法还是一样的．（1）已知关于x的多项式因式分解以后有一个因式为，试求m的值，并将多项式因式分解． （2）若是的一个因式，求pq的值．（1）由题意可知，，由一次项系数可得， ∴原式．（2）∵的三次项与一次项系数均为0，∴∴，∴．【教师备课提示】这道题主要是想让学生们理解什么叫做待定系数法．
（1）已知多项式能分解为两个一次因式的乘积，求k的值． （2）当m取何值时，多项式可以分解成两个一次因式的积．（1）因为，故可设，即，比较对应项系数得，，，解得．（2），∴设∴，∴．因式分解：（1）     （2）（1）原式的有理根只能为，，经检验都不能使得原式为0，所以原式不含有一次因式，只含有二次因式，所以令或当时，则由题得，解得由于分解是唯一的，所以原式．（2）原式的有理根只能为，，经检验都不能使得原式为0，所以原式不含有一次因式，只含有二次因式，所以令或当时，\则由题得，解得由于分解是唯一的，所以原式．
因式分解：（1）      （2）（1）系数和为0，则原式．（2）偶数项系数和等于奇数项系数和，则原式．因式分解：原式的有理数根只可能为：，，，，经检验和使得原式为0，所以原式有因式，，原式．分解因式：．∵∴是原式的因式，并且．
已知关于x的多项式因式分解以后有一个因式为，试求m的值，并将多项式因式分解．由题意可知，，由一次项系数可得．所以，原式．因式分解：．原式的有理根只能为，，经检验都不能使得原式为0，所以原式不含有一次因式，只含有二次因式，所以令或当时，则由题得，解得由于分解是唯一的，所以原式．