北师大版八年级上册5 应用二元一次方程组——里程碑上的数优质ppt课件

这是一份北师大版八年级上册5 应用二元一次方程组——里程碑上的数优质ppt课件，共32页。PPT课件主要包含了素养目标，解法一，解法二，解法三，课后作业等内容，欢迎下载使用。

《孙子算经》是我国古代一部较为普及的算书,许多问题浅显有趣,其中下卷第31题“雉兔同笼”流传尤为广泛,飘洋过海流传到了日本等国.
今有鸡兔同笼, 上有三十五头, 下有九十四足, 问鸡兔各几何?
你有哪些方法来解决它呢？
1. 通过小组合作，分析“鸡兔同笼”等简单问题中的数量关系，学生能准确找出等量关系.
2. 掌握列二元一次方程组解决实际问题的一般步骤.
3. 通过交流，体会我国古代数学的光辉成就，体验古代数学的趣味性，激发学生对数学的好奇心和求知欲.
“鸡兔同笼”题为: “今有雉(鸡)兔同笼, 上有三十五头, 下有九十四足, 问雉兔各几何?”
（1） “上有三十五头”的意思是什么?
“下有九十四足”的意思是什么?
（2）题中有哪些等量关系?
（3）你能解决这个有趣的问题吗?
列二元一次方程组解答实际问题
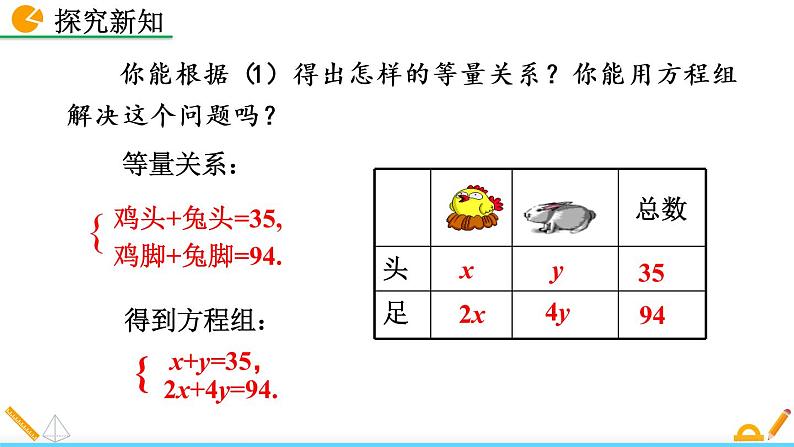
你能根据（1）得出怎样的等量关系？你能用方程组解决这个问题吗？
设鸡为x只,兔为y只.则
解法一: (加减消元法) ①×2 得： 2x+2y=70 ③
②-③得：2y=24，
把 y=12 代入①，得：x=23
所以有鸡23只，兔12只.
解法二: （代入消元法）由①得，x =35- y ③
把③代入②，得2（35- y）+4y=94,
把y=12代入①，得x=23
所以鸡有23只，兔子有12只．
设鸡为x只,兔为y 只.则
归纳：列二元一次方程组解决实际问题的一般步骤审：弄清题意和题目中的数量关系，找出题目中的等量关系；设：用字母表示题目中的两个未知数；列：根据找出的等量关系列出方程组；解：解方程组，求得未知数的值；验：检验所得的解是否是方程组的解，并且要检验其是否符合实际问题的意义，不符合要舍去；答：写出答案，包括单位名称.
以绳测井.若将绳三折测之，绳多五尺；若将绳四折测之，绳多一尺.绳长、井深各几何？
题意：用绳子测量水井的深度.如果将绳子折成三等份，一份绳长比井深多5尺；如果将绳子折成四等份，一份绳长比井深多1尺.绳长、井深各是多少尺？
列二元一次方程组解答较简单问题
解：设绳长x尺，井深y尺，则由题意得 解得x = 48 将x = 48代入① 得 y = 11 答：绳长48尺，井深11尺.
等量关系： （井深+5）× 3 = 绳长 （井深+1）× 4 = 绳长 解：设绳长x尺，井深y尺，则由题意得 3 (y+5) = x 4 (y+1) = x 答：绳长48尺，井深11尺.
等量关系： 绳长 — 井深的3倍= 3 ×5 绳长 — 井深的4倍= 4 ×1解：设绳长x尺，井深y尺，则由题意得 x - 3y = 3 ×5 x - 4y = 4 ×1答：绳长48尺，井深11尺.
养牛场原有30只大牛和15只小牛，1天约用饲料675 kg；一周后又购进12只大牛和5只小牛，这时1天约用饲料940 kg.饲养员李大叔估计每只大牛1天约需饲料18到20 kg，每只小牛1天约需饲料7到8 kg.你认为李大叔估计的准确吗？
分析1： 题中有哪些未知量，你如何设未知数？
未知量:每头大牛1天需用的饲料;每头小牛1天需用的饲料.
分析2：题中有哪些等量关系？
(1)30只大牛和15只小牛一天需用饲料为675kg;
(2)(30+12)只大牛和(15+5)只小牛一天需用饲料为940kg.
设未知数：设每头大牛和每头小牛平均1天各需用饲料为xkg和ykg.
解:设每头大牛和小牛平均1天各需用饲料为xkg和ykg，
根据等量关系，列方程组：
答:每头大牛和每头小牛1天各需用饲料为20kg和5kg，饲养员李大叔估计每天大牛需用饲料18到20千克，每头小牛一天需用7到8千克与计算有一定的出入.
+ = 675,
+ = 940.
据统计资料，甲、乙两种作物的单位面积产量的比1:2．现要把一块长200m、宽100m的长方形土地，分为两块小长方形土地，分别种植这两种作物．怎样划分这块土地，使甲、乙两种作物的总产量的比是3:4？
列二元一次方程组解答几何问题
已知：长方形ABCD， AB=CD=200m，AD=BC=100m，长方形ABCD分割为两个小长方形，长方形1和长方形2分别种甲、乙作物，甲、乙单位面积产量的比是1:2.
这里研究的实际上是什么问题？
把一个长方形分成两个小长方形有哪些分割方式？
竖着画，把长分成两段，则宽不变
横着画，把宽分成两段，则长不变
我们可以画出示意图来帮助分析
目标：甲、乙两种作物的总产量的比是3:4
1.大长方形的长=200m
2.甲、乙两种作物总产量比=3:4
设AE＝xm，BE＝ym.
再写出两种作物的总产量
100x:200y=3:4
根据题意列方程组为
过点E作EF⊥AB，交CD于点F.
设AE＝xm，BE＝ym.
答：将这块土地分为长120m,宽100m和长100m,宽80m的两个小长方形分别种植甲、乙两种作物.
解：过点E作EF⊥BC，交BC于点F. 设DE＝xm，AE＝ym.
200x:400y=3:4
答：将这块土地分为长200m,宽60m和长200m,宽40m的两个小长方形分别种植甲、乙两种作物.
8块相同的小长方形地砖拼成一个大长方形，每块小长方形地砖的长和宽分别是多少?（单位cm）
解:设小长方形地砖的长为x, 宽为y, 由题意,得
答:小长方形地砖的长为45cm, 宽为15cm.
（2019•舟山）中国清代算书《御制数理精蕴》中有这样一题：“马四匹、牛六头，共价四十八两（我国古代货币单位）；马三匹、牛五头，共价三十八两．问马、牛各价几何？”设马每匹x两，牛每头y两，根据题意可列方程组为（　　） A． B． C． D．
1.某校春季运动会比赛中，八年级（1）班、（5）班的竞技实力相当，关于比赛结果，甲同学说：（1）班与（5）班得分比为6:5；乙同学说：（1）班得分比（5）班得分的2倍少40分．若设（1）班得x分，（5）班得y分，根据题意所列的方程组应为（ ）
B.C. D.
2.一只蛐蛐6条腿，一只蜘蛛8条腿，现有蛐蛐和蜘蛛共10只，共有68条腿，若设蛐蛐有x只，蜘蛛有y只，则列出方程组为______________．
解析:根据蛐蛐和蜘蛛共10只，可得x＋y＝10; 蛐蛐和蜘蛛共有68条腿，可得6x＋8y＝68.
3.某电脑经销商计划同时购进一批电脑机箱和液晶显示器，若购进电脑机箱10台和液晶显示器8台，共需资金7 000元；若购进电脑机箱2台和液晶显示器5台，共需资金4 120元．则每台电脑机箱和液晶显示器的进价各多少元？
解：设每台电脑机箱和液晶显示器的进价分别为x元和y元， 答：每台电脑机箱和液晶显示器的进价分别是60元、800元．
某校现有校舍20000m2计划拆除部分旧校舍，改建新校舍，使校舍总面积增加30%.若建造新校舍的面积为被拆除的旧校舍面积的4倍，那么应该拆除多少旧校舍，建造多少新校舍？（单位为m2 ）
解：设应拆除旧校舍xm2，建造新校舍ym2 ，
由题意得：解得：答：应该拆除2000m2旧校舍，建造8000m2新校舍.
100匹马恰好拉了100片瓦，已知一匹大马能拉3片瓦，3匹小马能拉一片瓦，问有多少匹大马、多少匹小马？
解:设有x匹大马, y匹小马, 根据题意,得
答：有25匹大马，75匹小马.
审题：弄清题意和题目中的
设元：用_____ 表示题目中的未知数
列方程组:根据__个等量关系列出方程组