初中北师大版2 定义与命题完美版ppt课件

这是一份初中北师大版2 定义与命题完美版ppt课件，共32页。PPT课件主要包含了素养目标，两点之间的距离，中华人民共和国公民，交流探究，1对顶角相等吗，命题的识别，已知事项，由已知事项推出的事项，题设条件，命题的组成等内容，欢迎下载使用。

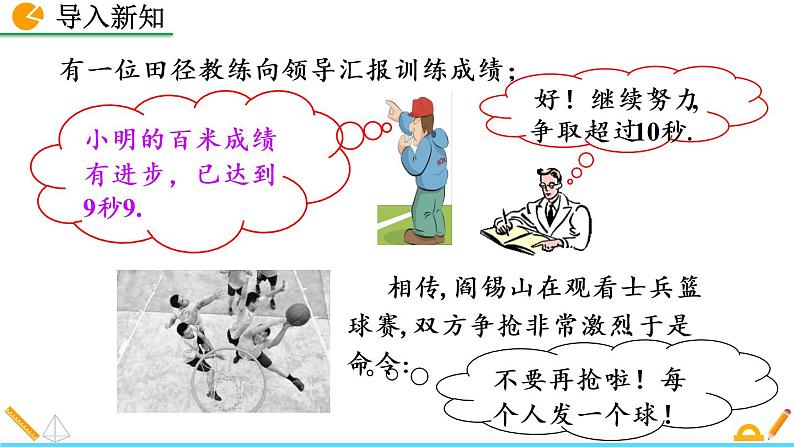
小明的百米成绩有进步，已达到9秒9.
好！继续努力,争取超过10秒.
不要再抢啦！每个人发一个球！
有一位田径教练向领导汇报训练成绩；
相传,阎锡山在观看士兵篮球赛,双方争抢非常激烈.于是命令:
1. 理解定义、命题的概念，能区分命题的条件和结论，并把命题写成“如果……那么……”的形式.
2.了解真命题和假命题的概念，能判断一个命题的真假性，并会对假命题举反例．
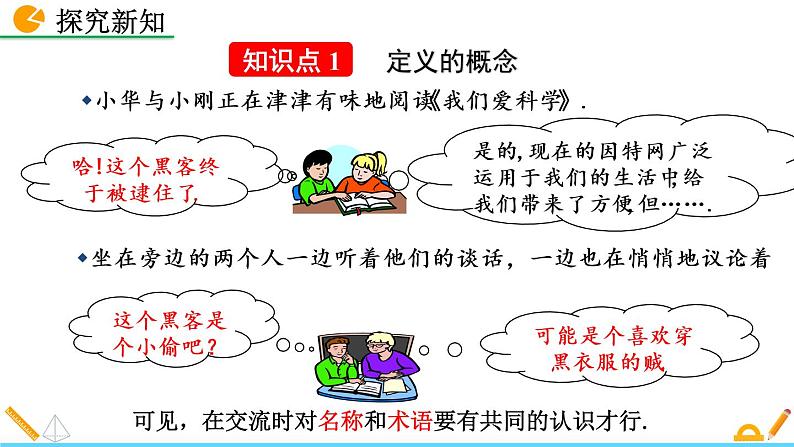
小华与小刚正在津津有味地阅读《我们爱科学》.
坐在旁边的两个人一边听着他们的谈话，一边也在悄悄地议论着.
哈!这个黑客终于被逮住了.
是的,现在的因特网广泛运用于我们的生活中,给我们带来了方便,但…….
可能是个喜欢穿黑衣服的贼.
可见，在交流时对名称和术语要有共同的认识才行.
人与人之间的交流必须对某些名词或术语有共同的认识才能正常进行.为此人们对各个名词或术语的含义，都给予了尽量详细的描述，做出了明确的规定，也就是给出了它们的定义.
例如:1.“具有中华人民共和国国籍的人,叫做中华人民共和国公民” 是“ ”的定义;
2. “两点之间 线段的长度,叫做这两点之间的距离” 是“ ”的定义;
　 一般地，能清楚地规定某一名称或术语的意义的句子叫做该名称或术语的定义．
请说出下列名词的定义：⑴无理数：⑵直角三角形：⑶一次函数：⑷二元一次方程：
无限不循环小数叫做无理数.
有一个角是直角的三角形叫做直角三角形.
一般地，形如y＝kx＋b（k、b都是常数且k≠0）叫做一次函数.
含有两个未知数，并且所含未知数的项的次数都是1的方程
说一说 你还学过哪些名词或术语的定义？
下面的语句中，哪些语句对事情作出了判断，哪些没有？与同伴进行交流.（1）任何一个三角形一定有一个角是直角；（2）对顶角相等；（3）无论n为怎样的自然数，式子 的值 都是质数；（4）如果两条直线都和第三条直线平行，那么这两条直线也互相平行；（5）你喜欢数学吗？（6）作线段AB=CD.
命题的定义：判断一件事情的句子.
（1）（2）（3）（4）都是命题.你能再举几个例子吗？
下面的语句中，哪些语句是命题？（1）你喜欢学习吗？（2）作线段AB=a.（3）平行用符号“∥”表示.
一般情况下，疑问句不是命题，图形的作法不是命题，祈使句也不是命题！
2.如果一个句子没有对某一件事情作出任何判断,那么 它就不是命题.
如：画线段AB=CD.
1.只要对一件事情作出了判断,不管正确与否,都是命题.
如：相等的角是对顶角.
例 判断下列四个语句中，哪个是命题， 哪个不是命题？并说明理由：
（2）画一条线段AB=2cm;
（3）两条直线平行，同位角相等；
（4）相等的两个角，一定是对顶角.
解：（3）（4）是命题，（1）（2）不是命题.理由如下：（1）是问句，故不是命题；（2）是做一件事情，也不是命题.
下列语句在表述形式上，哪些是命题？哪些不是命题？1. 等角的余角相等；2. 画一个角等于已知角；3. 两直线平行，内错角相等；4. a , b两条直线平行吗？5. 温柔的李明明；6. 玫瑰花是动物；7. 若a2＝4，求a的值；8. 若a2＝b2，则a＝b.
观察下列命题，这些命题有什么共同的结构特征:（1）如果一个三角形是等腰三角形，那么这个三角形的两个底角相等；（2）如果a=b，那么a2=b2；（3）如果两个三角形中有两边和一个角分别相等，那么这两个三角形全等.
命题的形式：如果……那么…….
命题的结构：由条件和结论两部分组成.条件是已知的事项，结论是由已知事项推断出的事项.
“如果” 引出的部分是条件，“那么”引出的部分是结论.
有些命题没有写成“如果……那么……”的形式，条件和结论不明显，对于这样的命题，要经过分析才能找出条件和结论，也可以先将它们改写成“如果……那么……”的形式.
注意：命题的条件部分，有时也可用“已知……”或者“若……”等形式表述，命题的结论部分，有时也可用“求证……”或“则……”等形式表述.
两直线平行， 同位角相等
例 分别把下列命题写成“如果……那么……”的形式. (1)两点确定一条直线；(2)等角的补角相等；(3)内错角相等.
解：(1)如果有两个定点，那么过这两点有且只有一条直线；(2)如果两个角分别是两个等角的补角，那么这两个角相等；(3)如果两个角是内错角，那么这两个角相等.
请将它们改写成“如果……，那么……”的形式.（1）两条直线被第三条直线所截，同旁内角互补；（2）等式两边都加同一个数，结果仍是等式；（3）互为相反数的两个数相加得0；（4）同旁内角互补；（5）对顶角相等．
如果两条直线被第三条直线所截，那么同旁内角互补；
如果等式两边都加同一个数，那么结果仍是等式；
如果两个数互为相反数，那么这两个数相加得0；
如果两个角是同旁内角，那么这两个角互补；
如果两个角互为对顶角，那么这两个角相等．
有些命题如果题设成立，那么结论一定成立；而有些命题题设成立时，结论不一定成立.
正确的命题叫真命题，不正确的命题叫假命题.
如命题：“如果两个角互补，那么它们是邻补角”就是一个错误的命题.
如命题：“如果一个数能被4整除，那么它也能被2整除”就是一个正确的命题.
注意：要说明一个命题是假命题，只需举一个反例.反例是指具备命题的条件，而不具有命题的结论的例子.
例 下列命题哪些命题是正确的，哪些命题是错误的？（1）两条直线被第三条直线所截，同旁内角互补；（2）等式两边都加同一个数，结果仍是等式；（3）互为相反数的两个数相加得0；（4）同旁内角互补；（5）对顶角相等．
下列句子哪些是命题？是命题的，指出是真命题还是假命题？
（1）猪有四只脚； （2）内错角相等； （3）画一条直线； （4）四边形是正方形； （5）你的作业做完了吗？ （6）同位角相等，两直线平行； （7）同角的补角相等； （8）同垂直于一直线的两直线平行； （9）过点P画线段MN的垂线； （10）x＞2.
1.（2019•常州）判断命题“如果n＜1，那么n2﹣1＜0”是假命题，只需举出一个反例．反例中的n可以为（　　）A．﹣2B． C． 0 D．
2.（2019•泰州）命题“三角形的三个内角中至少有两个锐角”是　_________（填“真命题”或“假命题”）．
1.下列语句中，属于定义的是（ ）A.两点确定一条直线； B.同角的余角相等；C.互补的两个角是邻补角； D.点到直线的距离是该点到这条直线的垂线段的长度.
2. 下列命题：①两点确定一条直线；②两点之间，线段最短；③对顶角相等；④内错角相等；其中真命题的个数是 ( )A. 1个 B. 2个 C. 3个 D. 4个
3.如图所示，从①∠1＝∠2 ②∠C＝∠D ③∠A＝∠F 三个条件中选出两个作为已知条件，另一个作为结论所组成的命题中，正确命题的个数为( ) A. 0 B. 1 C. 2 D. 3
4. 下列选项中，可以用来说明命题“两个锐角的和是锐角”是假命题的反例的是 ( )A. ∠A＝30°，∠B＝40° B. ∠A＝30°，∠B＝110°C. ∠A＝30°，∠B＝70° D. ∠A＝30°，∠B＝90°
5. 下列命题是真命题的是 ( )A. 相等的角是对顶角 B. 如果一个数能被3整除，那么它也能被6整除C. 同旁内角互补 D. 同位角相等，两直线平行
6. 如图所示，已知AC与BD相交于点O，OE是∠AOD的平分线，可以作为假命题“相等的角是对顶角”的反例的是( )A. ∠AOB＝∠DOC B. ∠EOC＜∠DOC C. ∠EOB＝∠EOC D. ∠EOC＞∠DOC
指出下列命题的条件和结论，并改写成“如果……那么……”的形式：
⑴三条边对应相等的两个三角形全等；
⑵在同一个三角形中，等角对等边；
如果两个三角形有三条边对应相等，那么这两个三角形全等.
如果两个角是同旁内角，那么这两个角相等.
(1)如图所示，若∠1＝∠2，则AB∥CD，试判断该命题的真假： (填“真”或“假”). (2)若上述命题为真命题，请说明理由，若上述命题为假命题，请你再添加一条件，使该命题成为真命题，并说明理由.
解：加条件：BE∥FD.理由如下：因为BE∥FD，所以∠EBD＝∠FDN(两直线平行，同位角相等).又因为∠1＝∠2，所以∠ABD＝∠CDN.所以AB∥CD(同位角相等，两直线平行).
概念：判断一个事件的句子
结构：如果……那么……