2021高考数学一轮复习统考第4章三角函数解三角形第3讲三角函数的图象与性质学案含解析北师大版

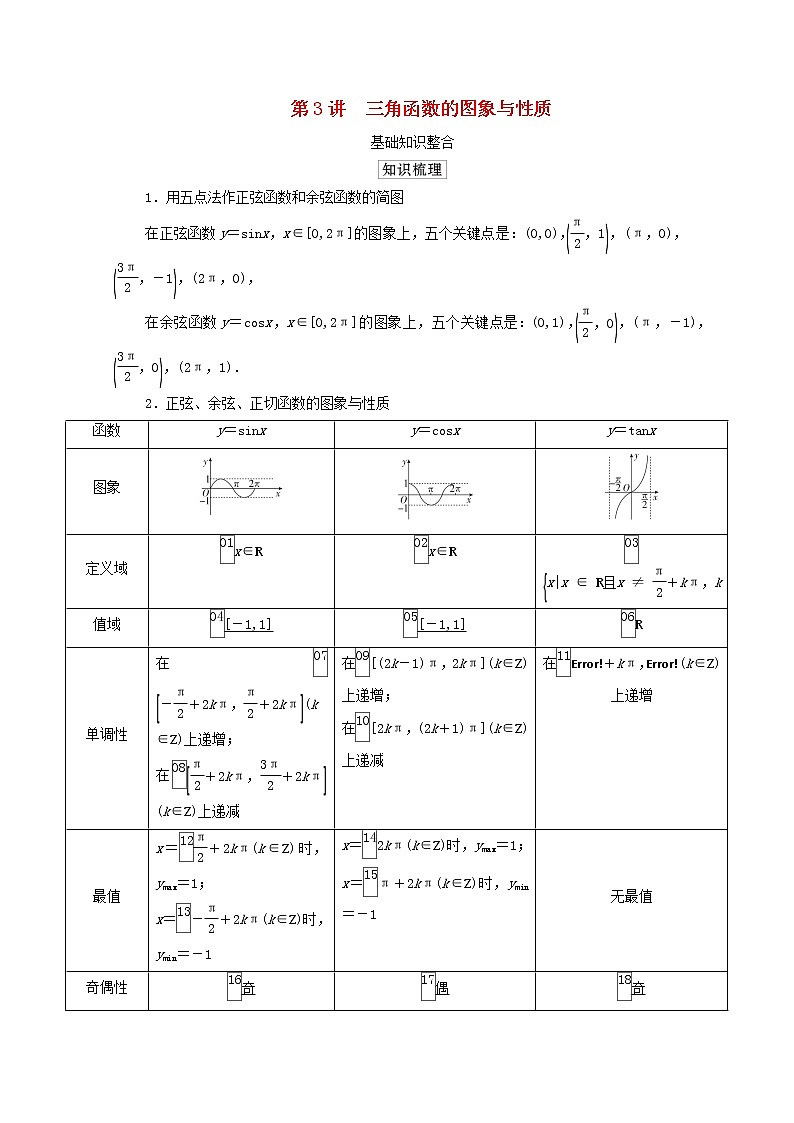
第3讲　三角函数的图象与性质基础知识整合1．用五点法作正弦函数和余弦函数的简图在正弦函数y＝sinx，x∈[0,2π]的图象上，五个关键点是：(0,0)，，(π，0)，，(2π，0)，在余弦函数y＝cosx，x∈[0,2π]的图象上，五个关键点是：(0,1)，，(π，－1)，，(2π，1)．2．正弦、余弦、正切函数的图象与性质函数y＝sinxy＝cosxy＝tanx图象定义域x∈Rx∈R值域[－1,1][－1,1]R单调性在(k∈Z)上递增；在(k∈Z)上递减在[(2k－1)π，2kπ](k∈Z)上递增；在[2kπ，(2k＋1)π](k∈Z)上递减在＋kπ，(k∈Z)上递增最值x＝＋2kπ(k∈Z)时，ymax＝1；x＝－＋2kπ(k∈Z)时，ymin＝－1x＝2kπ(k∈Z)时，ymax＝1；x＝π＋2kπ(k∈Z)时，ymin＝－1无最值奇偶性奇偶奇对称性对称中心(kπ，0)，k∈Z，k∈Z，k∈Z对称轴直线x＝kπ＋，k∈Z直线x＝kπ，k∈Z无对称轴最小正周期2π2ππ 1．函数y＝Asin(ωx＋φ)和y＝Acos(ωx＋φ)的最小正周期T＝，函数y＝tan(ωx＋φ)的最小正周期T＝.2．正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半周期，相邻的对称中心与对称轴之间的距离是周期．正切曲线相邻两对称中心之间的距离是半周期．3．三角函数中奇函数一般可化为y＝Asinωx或y＝Atanωx的形式，偶函数一般可化为y＝Acosωx＋b的形式．4．若f(x)＝Asin(ωx＋φ)(A≠0，ω≠0)，则：(1)f(x)为偶函数的充要条件是φ＝＋kπ(k∈Z)；(2)f(x)为奇函数的充要条件是φ＝kπ(k∈Z)．　 　　　　　　　　　　　　　　　　　　　　1．函数y＝tan的定义域是(　　)A.B.C.D.答案　D解析　y＝tan＝－tan，由x－≠＋kπ，k∈Z，得x≠kπ＋，k∈Z.故选D.2．(2019·江西六校联考)下列函数中，最小正周期是π且在区间上是增函数的是(　　)A．y＝sin2x   B．y＝sinxC．y＝tan   D．y＝cos2x答案　D解析　y＝sin2x在区间上的单调性是先减后增；y＝sinx的最小正周期是T＝＝2π；y＝tan的最小正周期是T＝＝2π；y＝cos2x满足条件．故选D.3．(2018·全国卷Ⅰ)已知函数f(x)＝2cos2x－sin2x＋2，则(　　)A．f(x)的最小正周期为π，最大值为3        B．f(x)的最小正周期为π，最大值为4 C．f(x)的最小正周期为2π，最大值为3      D．f(x)的最小正周期为2π，最大值为4答案　B解析　根据题意，有f(x)＝cos2x＋，所以函数f(x)的最小正周期为T＝＝π，且最大值为f(x)max＝＋＝4.故选B.4．(2019·长沙模拟)函数y＝sin，x∈[－2π，2π]的单调递增区间是(　　)A.   B．和C.   D．答案　C解析　令z＝x＋，函数y＝sinz的单调递增区间为(k∈Z)，由2kπ－≤x＋≤2kπ＋(k∈Z)，得4kπ－≤x≤4kπ＋(k∈Z)，又因为x∈[－2π，2π]，故其单调递增区间是.故选C.5．(2019·衡水中学调研)函数f(x)＝sin在区间上的最小值为(　　)A．－1   B．－  C.   D．0答案　B解析　由已知x∈，得2x－∈，所以sin∈，故函数f(x)＝sin在区间上的最小值为－.6．函数y＝3－2cos的最大值为________，此时x＝________.答案　5　＋2kπ(k∈Z)解析　函数y＝3－2cos的最大值为3＋2＝5，此时x＋＝π＋2kπ(k∈Z)，即x＝＋2kπ(k∈Z)． 核心考向突破考向一　三角函数的定义域　例1　(1)(2019·烟台模拟)函数y＝的定义域为(　　)A.B.(k∈Z)C.(k∈Z)D．R答案　C解析　由cosx－≥0，得cosx≥，∴2kπ－≤x≤2kπ＋，k∈Z.(2)(2019·江苏无锡模拟)函数y＝lg sin2x＋的定义域为________．答案　∪解析　由得∴－3≤x＜－或0＜x＜.∴函数y＝lg sin2x＋的定义域为∪.  (1)求三角函数的定义域常常归结为解三角不等式(或等式)． (2)求三角函数的定义域经常借助两个工具，即单位圆中的三角函数线和三角函数的图象，有时也利用数轴． (3)对于较为复杂的求三角函数的定义域问题，应先列出不等式(组)分别求解，然后利用数轴或三角函数线求交集．  [即时训练]　1.函数y＝的定义域为(　　)A.B.(k∈Z)C.(k∈Z)D.(k∈Z)答案　B解析　由2sinx－1≥0，得sinx≥，所以2kπ＋≤x≤2kπ＋(k∈Z)．2．函数y＝lg (sinx－cosx)的定义域是________．答案　解析　要使函数有意义，必须使sinx－cosx>0.解法一：利用图象．在同一坐标系中画出[0,2π]上y＝sinx和y＝cosx的图象，如图所示：在[0,2π]内，满足sinx＝cosx的x为，，在内sinx>cosx，再结合正弦、余弦函数的周期是2π，所以定义域为. 解法二：利用三角函数线．如图，MN为正弦线，OM为余弦线，要使sinx>cosx，只须<x<(在[0,2π]内)．所以定义域为.解法三：sinx－cosx＝sin>0，由正弦函数y＝sinx的图象和性质可知2kπ<x－<π＋2kπ，k∈Z，解得＋2kπ<x<＋2kπ，k∈Z.所以定义域为.考向二　三角函数的值域　 　　例2　(1)函数f(x)＝3sin在上的值域为________．答案　解析　当x∈时，2x－∈，sin∈，故3sin∈，∴函数f(x)在上的值域是.(2)设x∈，函数y＝4sin2x－12sinx－1的值域为________．答案　[－9,6]解析　令t＝sinx，由于x∈，故t∈，所以y＝4t2－12t－1＝42－10，因为当t∈时，函数单调递减，所以当t＝－，即x＝－时，ymax＝6；当t＝1，即x＝时，ymin＝－9.则函数的值域为[－9,6]．(3)函数y＝sinx－cosx＋sinxcosx，x∈[0，π]的最大值与最小值的差为________．答案　2解析　令t＝sinx－cosx，又x∈[0，π]，∴t＝sin，t∈[－1，]．由t＝sinx－cosx，得t2＝1－2sinxcosx，即sinxcosx＝.∴原函数变为y＝t＋，t∈[－1，]．即y＝－t2＋t＋.∴当t＝1时，ymax＝－＋1＋＝1；当t＝－1时，ymin＝－－1＋＝－1.故函数的最大值与最小值的差为2. 三角函数值域的求法(1)利用y＝sinx和y＝cosx的值域直接求．(2)把所给的三角函数式变换成y＝Asin(ωx＋φ)＋b(或y＝Acos(ωx＋φ)＋b)的形式求值域．(3)把sinx或cosx看作一个整体，将原函数转换成二次函数求值域，如y＝asin2x＋bsinx＋c，可先设sinx＝t，转换为关于t的二次函数求值域．(4)利用sinx±cosx和sinxcosx的关系将原函数转换成二次函数求值域．  [即时训练]　3.函数y＝2sin(0≤x≤9)的最大值与最小值之和为________．答案　2－解析　∵0≤x≤9，∴－≤x－≤，∴－≤sin≤1，故－≤2sin≤2.即函数y＝2sin(0≤x≤9)的最大值为2，最小值为－.∴函数的最大值与最小值的和为2－.4．(2017·全国卷Ⅱ)函数f(x)＝sin2x＋cosx－的最大值是________．答案　1解析　f(x)＝1－cos2x＋cosx－＝－2＋1.∵x∈，∴cosx∈[0,1]，∴当cosx＝时，f(x)取得最大值，最大值为1.精准设计考向，多角度探究突破考向三　三角函数的性质角度1　　三角函数的奇偶性　 　　　　　　　　　　　　　　　　　　　　例3　(1)已知函数y＝2sin是偶函数，则θ的值为(　　)A．0   B．  C.   D．答案　B解析　因为函数f(x)为偶函数，所以θ＋＝kπ＋(k∈Z)．又θ∈，所以θ＋＝，解得θ＝，经检验符合题意．故选B.(2)(2019·哈尔滨模拟)若函数y＝3cos为奇函数，则|φ|的最小值为________．答案　解析　依题意得，－＋φ＝kπ＋(k∈Z)，φ＝kπ＋(k∈Z)，因此|φ|的最小值是.角度2　　三角函数的对称性　 　例4　(1)(2019·东北三省四市联考)已知函数f(x)＝2sin(ω>0)的最小正周期为π，则下列选项正确的是(　　)A．函数f(x)的图象关于点对称B．函数f(x)的图象关于点对称C．函数f(x)的图象关于直线x＝对称D．函数f(x)的图象关于直线x＝－对称答案　B解析　设函数f(x)的最小正周期为T，依题意得T＝＝π，ω＝2，f(x)＝2sin.f＝2sin＝2≠0，因此函数f(x)的图象不关于点对称，A不正确．f＝2sin＝0，因此函数f(x)的图象关于点对称，B正确，D不正确．f＝2sin＝1≠±2，因此函数f(x)的图象不关于直线x＝对称，C不正确．综上所述，选B.(2)(2018·江苏高考)已知函数y＝sin(2x＋φ)的图象关于直线x＝对称，则φ的值是________．答案　－解析　∵函数y＝sin(2x＋φ)的图象关于直线x＝对称，∴x＝时，函数取得最大值或最小值，∴sin＝±1.∴＋φ＝kπ＋(k∈Z)，∴φ＝kπ－(k∈Z)，又－<φ<，∴φ＝－.角度3　　三角函数的单调性　　例5　(1)函数y＝2sin(x∈[0，π])的增区间是(　　)A.   B．C.   D．答案　C解析　∵y＝2sin＝－2sin，由＋2kπ≤2x－≤＋2kπ，k∈Z，解得＋kπ≤x≤＋kπ，k∈Z，即函数的增区间为，k∈Z，∴当k＝0时，增区间为.(2)已知ω>0，函数f(x)＝sin在上单调递减，则ω的取值范围是(　　)A.   B．C.   D．(0,2)答案　A解析　由2kπ＋≤ωx＋≤2kπ＋(k∈Z)，得＋≤x≤＋(k∈Z)．∵f(x)＝sin在上单调递减，∴解得令k＝0，得≤ω≤.故选A.  1．三角函数型奇偶性判断除可以借助定义外，还可以借助其图象的性质，对y＝Asin(ωx＋φ)，代入x＝0，若y＝0则为奇函数，若y为最大值或最小值则为偶函数．2．求函数y＝Asin(ωx＋φ)的对称中心、对称轴问题往往转化为解方程问题(1)∵y＝sinx的对称中心是(kπ，0)，k∈Z，∴y＝Asin(ωx＋φ)的对称中心，由方程ωx＋φ＝kπ解出x即可．(2)∵y＝sinx的对称轴是直线x＝kπ＋，k∈Z，∴由ωx＋φ＝kπ＋解出x，即可得到函数y＝Asin(ωx＋φ)的对称轴．(3)注意y＝tanx的对称中心为(k∈Z)．3．求三角函数单调区间的两种方法(1)代换法：将比较复杂的三角函数解析式中含自变量的代数式(如ωx＋φ)整体当作一个角u(或t)，利用基本三角函数(y＝sinx、y＝cosx、y＝tanx)的单调性列不等式求解．(2)图象法：画出三角函数的图象，利用图象求函数的单调区间．提醒：要注意求函数y＝Asin(ωx＋φ)的单调区间时ω的符号，若ω<0，那么一定要先借助诱导公式将ω化为正数．同时切莫忘记考虑函数自身的定义域．4．利用单调性确定ω的范围的方法对于已知函数的单调区间的某一部分确定参数ω的范围的问题，首先，明确已知的单调区间应为函数的单调区间的子集，其次，要确定已知函数的单调区间，从而利用它们之间的关系求解，另外，若是选择题，利用特值验证、排除法求解更为简便．  [即时训练]　5.(2019·全国卷Ⅱ)下列函数中，以为周期且在区间单调递增的是(　　)A．f(x)＝|cos2x|   B．f(x)＝|sin2x|C．f(x)＝cos|x|   D．f(x)＝sin|x|答案　A解析　作出函数f(x)＝|cos2x|的图象，如图．由图象可知f(x)＝|cos2x|的周期为，在区间上单调递增．同理可得f(x)＝|sin2x|的周期为，在区间上单调递减，f(x)＝cos|x|的周期为2π.f(x)＝sin|x|不是周期函数，排除B，C，D.故选A.6．(2018·全国卷Ⅱ)若f(x)＝cosx－sinx在[－a，a]是减函数，则a的最大值是(　　)A.   B．  C.   D．π答案　A解析　∵f(x)＝cosx－sinx＝cos，∴由2kπ≤x＋≤π＋2kπ(k∈Z)得－＋2kπ≤x≤＋2kπ(k∈Z)，因此[－a，a]⊆.∴－a<a，－a≥－，a≤，∴0<a≤，从而a的最大值为，选A.7．若函数f(x)＝cos(2x＋φ)的图象关于点成中心对称，且－<φ<，则函数y＝f为(　　)A．奇函数且在内单调递增B．偶函数且在内单调递增C．偶函数且在内单调递减D．奇函数且在内单调递减答案　D解析　∵函数f(x)＝cos(2x＋φ)的图象关于点成中心对称，∴2×＋φ＝kπ＋(k∈Z)，∴φ＝kπ－.∵－<φ<，∴φ＝－，∴f(x)＝cos，∴f＝cos＝－sin2x，∴f为奇函数．由2kπ－≤2x≤2kπ＋(k∈Z)，解得kπ－≤x≤kπ＋.令k＝0得函数f的一个单调递减区间为，∴函数f在内单调递减．(2019·龙岩模拟)已知函数f(x)＝2asin＋a＋b的定义域是[0，]，值域是[－5,1]，求a，b的值．解　因为0≤x≤，所以≤2x＋≤，,－≤sin≤1.所以当a>0时，解得当a<0时，解得因此a＝2，b＝－5或a＝－2，b＝1.答题启示(1)对此类问题的解决，首先利用正弦函数、余弦函数的有界性或单调性求出y＝Asin(ωx＋φ)或y＝Acos(ωx＋φ)的最值，但要注意对A的正负进行讨论，以便确定是最大值还是最小值；(2)再由已知列方程求解；(3)本题的易错点是忽视对参数a>0或a<0的分类讨论，导致漏解．对点训练已知a是实数，则函数f(x)＝1＋asinax的图象不可能是(　　)答案　D解析　当a＝0时，f(x)＝1，即图象C；当0<a<1时，三角函数的最大值为1＋a<2，且最小正周期为T＝>2π，即图象A；当a>1时，三角函数的最大值为a＋1 >2，且最小正周期为T＝<2π，即图象B.