

2021高考数学一轮复习统考第8章立体几何第4讲直线平面平行的判定及性质学案含解析北师大版
展开第4讲 直线、平面平行的判定及性质
基础知识整合
1.直线与平面平行
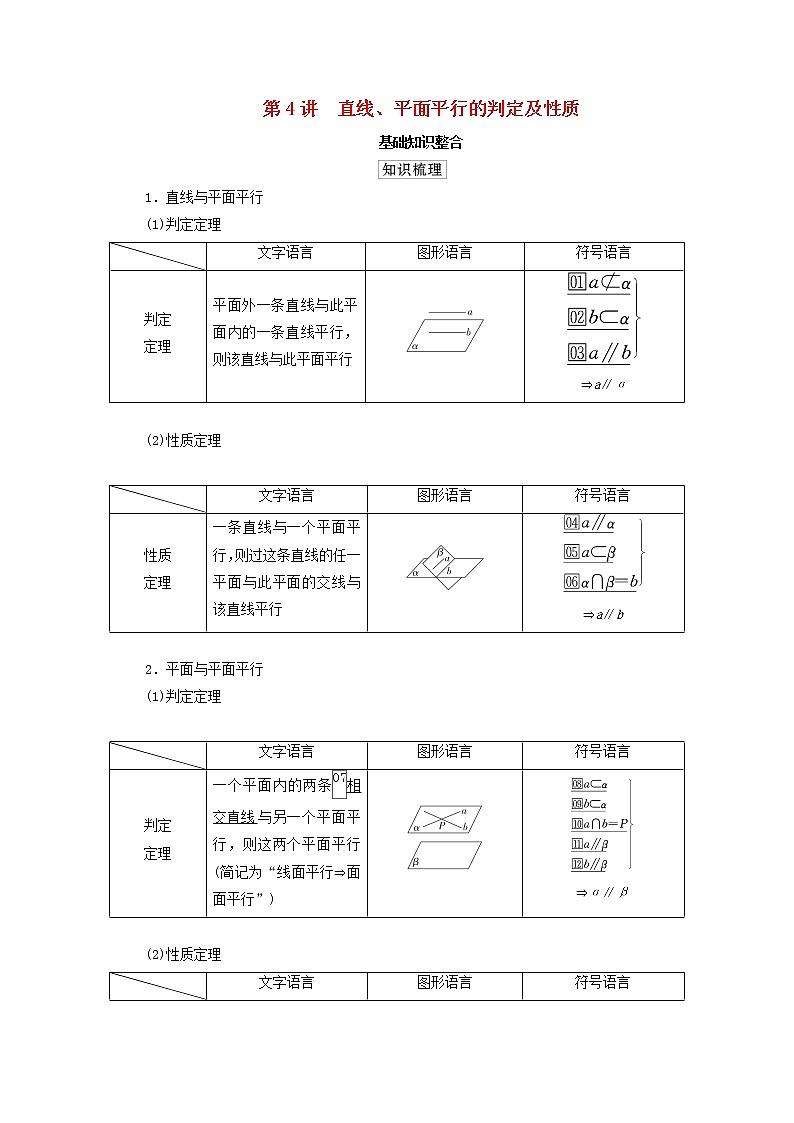
(1)判定定理
| 文字语言 | 图形语言 | 符号语言 |
判定 定理 | 平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行 |
⇒a∥α |
(2)性质定理
| 文字语言 | 图形语言 | 符号语言 |
性质 定理 | 一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行 | ⇒a∥b |
2.平面与平面平行
(1)判定定理
| 文字语言 | 图形语言 | 符号语言 |
判定 定理 | 一个平面内的两条相交直线与另一个平面平行,则这两个平面平行(简记为“线面平行⇒面面平行”) | ⇒α∥β |
(2)性质定理
| 文字语言 | 图形语言 | 符号语言 |
性质 定理 | 如果两个平行平面同时和第三个平面相交,那么它们的交线平行 | ⇒a∥b |
1.垂直于同一条直线的两个平面平行,即若a⊥α,a⊥β,则α∥β.
2.垂直于同一个平面的两条直线平行,即若a⊥α,b⊥α,则a∥b.
3.平行于同一个平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.
4.两个平面平行,其中一个平面内的任意一条直线平行于另一个平面.
5.夹在两个平行平面之间的平行线段长度相等.
6.经过平面外一点有且只有一个平面与已知平面平行.
7.两条直线被三个平行平面所截,截得的对应线段成比例.
8.如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行.
1.已知直线l和平面α,若l∥α,P∈α,则过点P且平行于l的直线( )
A.只有一条,不在平面α内
B.只有一条,且在平面α内
C.有无数条,一定在平面α内
D.有无数条,不一定在平面α内
答案 B
解析 过直线外一点作该直线的平行线有且只有一条,因为点P在平面α内,所以这条直线也应该在平面α内.
2.(2019·全国卷Ⅱ)设α,β为两个平面,则α∥β的充要条件是( )
A.α内有无数条直线与β平行
B.α内有两条相交直线与β平行
C.α,β平行于同一条直线
D.α,β垂直于同一平面
答案 B
解析 若α∥β,则α内有无数条直线与β平行,反之不成立;若α,β平行于同一条直线,则α与β可以平行也可以相交;若α,β垂直于同一平面,则α与β可以平行也可以相交,故A,C,D均不是充要条件.根据平面与平面平行的判定定理知,若一个平面内有两条相交直线与另一个平面平行,则这两个平面平行,反之也成立.因此B中的条件是α∥β的充要条件.故选B.
3.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )
答案 A
解析 A项,作如图①所示的辅助线,其中D为BC的中点,则QD∥AB.∵QD∩平面MNQ=Q,∴QD与平面MNQ相交,∴直线AB与平面MNQ相交.B项,作如图②所示的辅助线,则AB∥CD,CD∥MQ,∴AB∥MQ.又AB⊄平面MNQ,MQ⊂平面MNQ,∴AB∥平面MNQ.
C项,作如图③所示的辅助线,则AB∥CD,CD∥MQ,∴AB∥MQ.又AB⊄平面MNQ,MQ⊂平面MNQ,
∴AB∥平面MNQ.D项,作如图④所示的辅助线,则AB∥CD,CD∥NQ,∴AB∥NQ.又AB⊄平面MNQ,NQ⊂平面MNQ,∴AB∥平面MNQ.故选A.
4.如图所示,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点,给出下列五个结论:
①PD∥平面AMC;
②OM∥平面PCD;
③OM∥平面PDA;
④OM∥平面PBA;
⑤OM∥平面PBC.
其中正确的个数是( )
A.1 B.2
C.3 D.4
答案 C
解析 因为矩形ABCD的对角线AC与BD交于点O,所以O为BD的中点.在△PBD中,因为M为PB的中点,所以OM为△PBD的中位线,OM∥PD,所以PD∥平面AMC,OM∥平面PCD,且OM∥平面PDA.因为M∈PB,所以OM与平面PBA,平面PBC相交.
5.如图,平面α∥平面β,△PAB所在的平面与α,β分别交于CD,AB,若PC=2,CA=3,CD=1,则AB=________.
答案
解析 ∵平面α∥平面β,∴CD∥AB,∴=,
∴AB===.
6.已知下列命题:
①若直线与平面有两个公共点,则直线在平面内;
②若直线l上有无数个点不在平面α内,则l∥α;
③若直线l与平面α相交,则l与平面α内的任意直线都是异面直线;
④如果两条异面直线中的一条与一个平面平行,则另一条直线一定与该平面相交;
⑤若直线l与平面α平行,则l与平面α内的直线平行或异面;
⑥若平面α∥平面β,直线a⊂α,直线b⊂β,则a∥b.
上述命题正确的是________.
答案 ①⑤
解析 ①若直线与平面有两个公共点,由公理1可得直线在平面内,故①正确;②若直线l上有无数个点不在平面α内,则l∥α或l与α相交,故②错误;③若直线l与平面α相交,则l与平面α内的任意直线可能是异面直线或相交直线,故③错误;④如果两条异面直线中的一条与一个平面平行,则另一条直线可能与该平面平行或相交或在平面内,故④错误;⑤若直线l与平面α平行,则l与平面α内的直线无公共点,即平行或异面,故⑤正确;⑥若平面α∥平面β,直线a⊂α,直线b⊂β,则a∥b或a,b异面,故⑥错误.
核心考向突破
考向一 有关平行关系的判断
例1 (1)(2019·福建厦门第二次质量检查)如图,在正方体ABCD-A1B1C1D1中,M,N,P分别是C1D1,BC,A1D1的中点,则下列命题正确的是( )
A.MN∥AP
B.MN∥BD1
C.MN∥平面BB1D1D
D.MN∥平面BDP
答案 C
解析 取B1C1的中点为Q,连接MQ,NQ,由三角形中位线定理,得MQ∥B1D1,∴MQ∥平面BB1D1D,由四边形BB1QN为平行四边形,得NQ∥BB1,∴NQ∥平面BB1D1D,∴平面MNQ∥平面BB1D1D,又MN⊂平面MNQ,∴MN∥平面BB1D1D,故选C.
(2)(2019·广东揭阳期末)已知两条不同的直线a,b,两个不同的平面α,β,有如下命题:
①若a∥α,b⊂α,则a∥b;
②若a∥α,b∥α,则a∥b;
③若α∥β,a⊂α,则a∥β;
④若α∥β,a⊂α,b⊂β,则a∥b.
以上命题正确的个数为( )
A.3 B.2
C.1 D.0
答案 C
解析 若a∥α,b⊂α,则a与b平行或异面,故①错误;若a∥α,b∥α,则a与b平行、相交或异面,故②错误;若α∥β,a⊂α,则a与β没有公共点,即a∥β,故③正确;若α∥β,a⊂α,b⊂β,则a与b无公共点,得a,b平行或异面,故④错误.∴正确的个数为1.故选C.
解决有关线面平行、面面平行的基本问题的注意点
(1)判定定理与性质定理中易忽视的条件,如线面平行的判定定理中,条件“线在面外”易忽视.
(2)结合题意构造或绘制图形,结合图形作出判断.
(3)举反例否定结论或用反证法推断命题是否正确.
[即时训练] 1.(2019·安徽江南十校综合素质检测)如图所示,正方体ABCD-A1B1C1D1中,点E,F,G,P,Q分别为棱AB,C1D1,D1A1,D1D,C1C的中点.则下列叙述中正确的是( )
A.直线BQ∥平面EFG
B.直线A1B∥平面EFG
C.平面APC∥平面EFG
D.平面A1BQ∥平面EFG
答案 B
解析 过点E,F,G的截面如图所示(其中H,I分别为AA1,BC的中点).
∵A1B∥HE,A1B⊄平面EFG,HE⊂平面EFG,
∴A1B∥平面EFG,故选B.
2.(2019·湖南联考)已知m,n是两条不同的直线,α,β,γ是三个不同的平面,下列命题中正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m∥α,m∥β,则α∥β
C.若α⊥γ,β⊥γ,则α∥β
D.若m⊥α,n⊥α,则m∥n
答案 D
解析 A中,两直线可能平行、相交或异面;B中,两平面可能平行或相交;C中,两平面可能平行或相交;D中,由线面垂直的性质定理可知结论正确,故选D.
精准设计考向,多角度探究突破
考向二 直线与平面平行的判定与性质
角度1 用线线平行证明线面平行
例2 (1)(2019·豫东名校联考)如图,在直四棱柱ABCD-A1B1C1D1中,E为线段AD上的任意一点(不包括A,D两点),平面CEC1与平面BB1D交于FG.
证明:FG∥平面AA1B1B.
证明 在直四棱柱ABCD-A1B1C1D1中,因为BB1∥CC1,BB1⊂平面BB1D,CC1⊄平面BB1D,
所以CC1∥平面BB1D.
又因为CC1⊂平面CEC1,平面CEC1与平面BB1D交于FG,
所以CC1∥FG.
因为BB1∥CC1,所以BB1∥FG.
而BB1⊂平面AA1B1B,FG⊄平面AA1B1B,
所以FG∥平面AA1B1B.
(2)(2019·山东日照模拟)如图,在三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.
求证:BD∥平面FGH.
证明 证法一:连接DG,CD,设CD∩GF=M,连接MH.在三棱台DEF-ABC中,由AB=2DE,G为AC的中点,可得DF∥GC,DF=GC,所以四边形DFCG为平行四边形,则M为CD的中点,又因为H为BC的中点,所以HM∥BD.
因为HM⊂平面FGH,BD⊄平面FGH,所以BD∥平面FGH.
证法二:在三棱台DEF-ABC中,由BC=2EF,H为BC的中点,可得BH∥EF,BH=EF,
所以四边形HBEF为平行四边形,BE∥HF.
在△ABC中,因为G为AC的中点,H为BC的中点,
所以GH∥AB.
又因为GH∩HF=H,所以平面FGH∥平面ABED.
因为BD⊂平面ABED,所以BD∥平面FGH.
角度 用线面平行证明线线平行
例3 如图所示,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.
求证:AP∥GH.
证明 如图所示,连接AC交BD于点O,连接MO,
∵四边形ABCD是平行四边形,
∴O是AC的中点,又M是PC的中点,∴AP∥OM.
又MO⊂平面BMD,PA⊄平面BMD,
∴PA∥平面BMD.
∵平面PAHG∩平面BMD=GH,
且PA⊂平面PAHG,∴PA∥GH.
1.判断或证明线面平行的常用方法
(1)利用线面平行的定义(无公共点).
(2)利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α).
(3)利用面面平行的性质(α∥β,a⊂α⇒a∥β).
(4)利用面面平行的性质(α∥β,a⊄α,a⊄β,a∥α⇒a∥β).
2.证明线线平行的3种方法
(1)利用平行公理(a∥b,b∥c⇒a∥c).
(2)利用线面平行的性质定理(a∥α,a⊂β,α∩β=b⇒a∥b).
(3)利用面面平行的性质定理(α∥β,α∩γ=a,β∩γ=b⇒a∥b).
[即时训练] 3.如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,PA=3,F是棱PA上的一个动点,E为PD的中点,O为AC的中点.
(1)求证:OE∥平面PAB;
(2)若AF=1,求证:CE∥平面BDF.
证明 (1)因为四边形ABCD为菱形,O为AC的中点,
所以O为BD的中点,
又因为E为PD的中点,
所以OE∥PB.
因为OE⊄平面PAB,PB⊂平面PAB,
所以OE∥平面PAB.
(2)过E作EG∥FD交AP于点G,连接CG,FO.
因为EG∥FD,EG⊄平面BDF,FD⊂平面BDF.
所以EG∥平面BDF.
因为E为PD的中点,EG∥FD,所以G为PF的中点,
因为AF=1,PA=3,所以F为AG的中点,
又因为O为AC的中点,所以OF∥CG.
因为CG⊄平面BDF,OF⊂平面BDF,
所以CG∥平面BDF.
因为EG∩CG=G,EG⊂平面CGE,CG⊂平面CGE,
所以平面CGE∥平面BDF,
又因为CE⊂平面CGE,所以CE∥平面BDF.
考向三 面面平行的判定与性质
例4 如图,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证:
(1)B,C,H,G四点共面;
(2)平面EFA1∥平面BCHG.
证明 (1)因为GH是△A1B1C1的中位线,所以GH∥B1C1.
又因为B1C1∥BC,
所以GH∥BC,所以B,C,H,G四点共面.
(2)因为E,F分别为AB,AC的中点,所以EF∥BC.
因为EF⊄平面BCHG,BC⊂平面BCHG,
所以EF∥平面BCHG.
因为A1G与EB平行且相等,
所以四边形A1EBG是平行四边形.所以A1E∥GB.
因为A1E⊄平面BCHG,GB⊂平面BCHG.
所以A1E∥平面BCHG.
因为A1E∩EF=E,所以平面EFA1∥平面BCHG.
证明面面平行的方法
(1)面面平行的定义.
(2)面面平行的判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
(3)利用垂直于同一条直线的两个平面平行.
(4)如果两个平面同时平行于第三个平面,那么这两个平面平行.
(5)利用“线线平行”“线面平行”“面面平行”的相互转化.
[即时训练] 4.如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,PA=2,AB=1.设M,N分别为PD,AD的中点.
(1)求证:平面CMN∥平面PAB;
(2)求三棱锥P-ABM的体积.
解 (1)证明:∵M,N分别为PD,AD的中点,
∴MN∥PA,
又MN⊄平面PAB,PA⊂平面PAB,
∴MN∥平面PAB.
在Rt△ACD中,∠CAD=60°,CN=AN,∴∠ACN=60°.
又∠BAC=60°,∴CN∥AB.
∵CN⊄平面PAB,AB⊂平面PAB,
∴CN∥平面PAB.
又CN∩MN=N,∴平面CMN∥平面PAB.
(2)由(1)知,平面CMN∥平面PAB,
∴点M到平面PAB的距离等于点C到平面PAB的距离.
∵AB=1,∠ABC=90°,∠BAC=60°,∴BC=,
∴三棱锥P-ABM的体积V=VM-PAB=VC-PAB=VP-ABC=××1××2=.








