2021高考数学一轮复习统考选修4_5不等式选讲课件试题（打包6套）北师大版选修4_5

选修4－5  不等式选讲

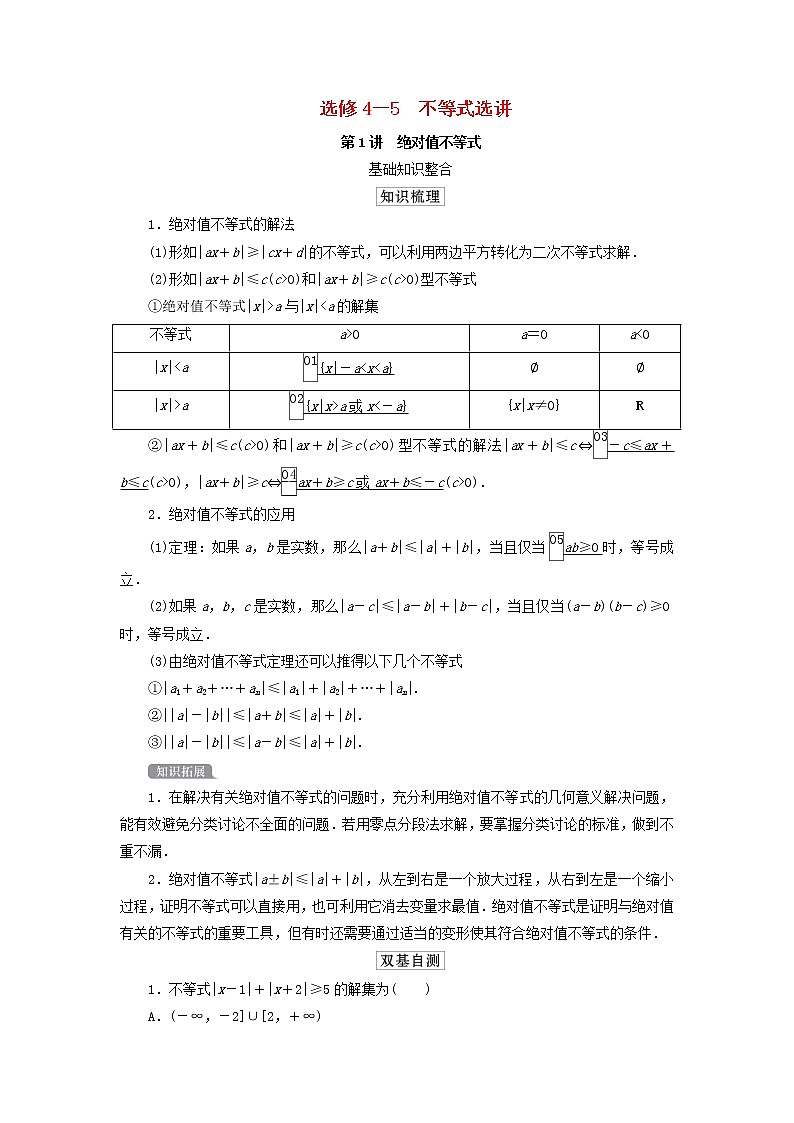
第1讲　绝对值不等式

基础知识整合

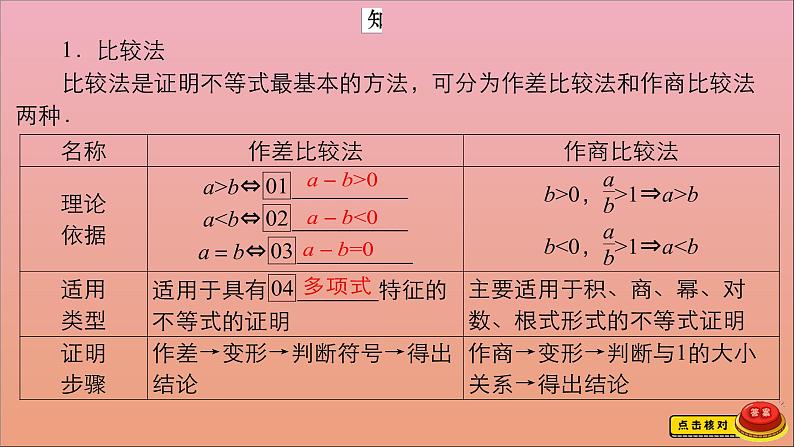
1．绝对值不等式的解法

(1)形如|ax＋b|≥|cx＋d|的不等式，可以利用两边平方转化为二次不等式求解．

(2)形如|ax＋b|≤c(c>0)和|ax＋b|≥c(c>0)型不等式

①绝对值不等式|x|>a与|x|<a的解集

②|ax＋b|≤c(c>0)和|ax＋b|≥c(c>0)型不等式的解法|ax＋b|≤c⇔－c≤ax＋b≤c(c>0)，|ax＋b|≥c⇔ax＋b≥c或ax＋b≤－c(c>0)．

2．绝对值不等式的应用

(1)定理：如果a，b是实数，那么|a＋b|≤|a|＋|b|，当且仅当ab≥0时，等号成立．

(2)如果a，b，c是实数，那么|a－c|≤|a－b|＋|b－c|，当且仅当(a－b)(b－c)≥0时，等号成立．

(3)由绝对值不等式定理还可以推得以下几个不等式

①|a1＋a2＋…＋an|≤|a1|＋|a2|＋…＋|an|.

②||a|－|b||≤|a＋b|≤|a|＋|b|.

③||a|－|b||≤|a－b|≤|a|＋|b|.

1．在解决有关绝对值不等式的问题时，充分利用绝对值不等式的几何意义解决问题，能有效避免分类讨论不全面的问题．若用零点分段法求解，要掌握分类讨论的标准，做到不重不漏．

2．绝对值不等式|a±b|≤|a|＋|b|，从左到右是一个放大过程，从右到左是一个缩小过程，证明不等式可以直接用，也可利用它消去变量求最值．绝对值不等式是证明与绝对值有关的不等式的重要工具，但有时还需要通过适当的变形使其符合绝对值不等式的条件．

1．不等式|x－1|＋|x＋2|≥5的解集为(　　)

A．(－∞，－2]∪[2，＋∞)

B．(－∞，－1]∪[2，＋∞)

C．(－∞，－2]∪[3，＋∞)

D．(－∞，－3]∪[2，＋∞)

答案　D

解析　原不等式等价于或

或即或或解得x≤－3或x∈∅或x≥2，所以x≤－3或x≥2.

2．若不等式|a－2x|≤x＋3对任意x∈[0,2]恒成立，则实数a的取值范围是(　　)

A．(－1,3)  B．[－1,3]

C．(1,3)  D．[1,3]

答案　B

解析　由题意可得当x∈[0,2]时，f(x)＝|a－2x|的图象恒在直线y＝x＋3的下方或在直线y＝x＋3上，如图，

所以得①或②

由①可得－1≤a<0，由②可得0≤a≤3，故实数a的取值范围是[－1,3]．

3．若关于x的不等式|x－m|＋|x＋2|<4的解集不为∅，则实数m的取值范围是(　　)

A．(－2,6)

B．(－∞，－2)∪(6，＋∞)

C．(－∞，－6)∪(2，＋∞)

D．(－6,2)

答案　D

解析　关于x的不等式|x－m|＋|x＋2|＜4的解集不为∅⇔(|x－m|＋|x＋2|)min＜4，∵|x－m|＋|x＋2|≥|(x－m)－(x＋2)|＝|m＋2|，∴|m＋2|＜4，解得－6＜m＜2，故选D.

4．若不等式|x＋1|－|2－x|<a无实数解，则a的取值范围是(　　)

A．(－∞，3)  B．(－3，＋∞)

C．(－∞，－3]  D．(－∞，－3)

答案　C

解析　由绝对值不等式的性质，得||x＋1|－|2－x||≤|(x＋1)＋(2－x)|＝3，即|x＋1|－|2－x|≥－3，因为|x＋1|－|2－x|<a无实数解，所以a≤－3，故选C.

5．不等式3≤|5－2x|<9的解集为(　　)

A．[－2,1)∪[4,7)  B．(－2,1]∪(4,7]

C．(－2，－1]∪[4,7)  D．(－2,1]∪[4,7)

答案　D

解析　由题意，得

⇒⇒

得所求不等式的解集为(－2,1]∪[4,7)．

6．不等式|x＋3|－|2x－1|<＋1的解集为________．

答案　

解析　①当x<－3时，原不等式化为－(x＋3)－(1－2x)<＋1，解得x<10，所以x<－3.

②当－3≤x＜时，原不等式化为(x＋3)－(1－2x)<＋1，解得x<－，所以－3≤x<－.

③当x≥时，原不等式化为x＋3＋1－2x<＋1，解得x>2，所以x>2.

综上可知，原不等式的解集为.

核心考向突破

考向一　绝对值不等式的解法

例1　(1)(2019·全国卷Ⅱ)已知f(x)＝|x－a|x＋|x－2|(x－a)．

①当a＝1时，求不等式f(x)<0的解集；

②若x∈(－∞，1)时，f(x)<0，求a的取值范围．

解　①当a＝1时，f(x)＝|x－1|x＋|x－2|(x－1)．

当x<1时，f(x)＝－2(x－1)2<0；

当x≥1时，f(x)≥0.

所以不等式f(x)<0的解集为(－∞，1)．

②因为f(a)＝0，所以a≥1.

当a≥1，x∈(－∞，1)时，f(x)＝(a－x)x＋(2－x)·(x－a)＝2(a－x)(x－1)<0.

所以a的取值范围是[1，＋∞)．

(2)(2019·河南八市压轴)已知函数f(x)＝|2x＋3|－|x－a|(a∈R)．

①当a＝1时，解不等式f(x)≥2；

②若关于x的不等式f(x)≥|x－3|的解集包含[3,5]，求a的取值范围．

解　①当a＝1时，不等式f(x)≥2，

即|2x＋3|－|x－1|≥2，

所以或或

解得x≤－6或x≥0，

所以不等式f(x)≥2的解集为(－∞，－6]∪[0，＋∞)．

②关于x的不等式f(x)≥|x－3|的解集包含[3,5]，

即|2x＋3|－|x－3|≥|x－a|在[3,5]上恒成立，

即x＋6≥|x－a|在[3,5]上恒成立，

即－6≤a≤2x＋6在x∈[3,5]上恒成立，

解得－6≤a≤12，所以a的取值范围是[－6,12]．

(1)分段讨论法：利用绝对值号内式子对应方程的根，将数轴分为(－∞，a]，(a，b]，(b，＋∞)(此处设a<b)三个部分，在每个部分上去掉绝对值符号分别列出对应的不等式求解，然后取各个不等式解集的并集．

(2)几何法：利用|x－a|＋|x－b|>c(c>0)的几何意义：数轴上到点x1＝a和x2＝b的距离之和大于c的全体．

(3)图象法：作出函数y1＝|x－a|＋|x－b|和y2＝c的图象，结合图象求解．

[即时训练]　1.(2019·湖北恩施质检)已知函数f(x)＝|x＋m|＋2|x－1|.

(1)当m＝2时，求不等式f(x)≤8的解集；

(2)若不等式f(x＋1)<3的解集为∅，求正数m的取值范围．

解　(1)当m＝2时，f(x)＝|x＋2|＋2|x－1|＝

当x<－2时，由－3x≤8，得x≥－，即－≤x<－2；当－2≤x≤1时，由－x＋4≤8，得x≥－4，即－2≤x≤1；当x>1时，由3x≤8，得x≤，即1<x≤.综上，不等式f(x)≤8的解集为.

(2)由f(x＋1)<3，得|x＋1＋m|＋2|x|<3，

令g(x) ＝|x＋1＋m|＋2|x|

＝

若不等式f(x＋1)<3的解集为∅，

则不等式f(x＋1)≥3的解集为R，

即g(x)min＝g(0)＝1＋m≥3，解得m≥2.

所以正数m的取值范围为[2，＋∞)．

2．(2020·广东佛山1月质量检测)已知函数f(x)＝|x－a|＋x，a∈R.

(1)若f(1)＋f(2)>5，求a的取值范围；

(2)若a，b∈N*，关于x的不等式f(x)<b的解集为，求a，b的值．

解　(1)由f(1)＋f(2)>5，得|1－a|＋|2－a|>2，

当a≥2时，a－1＋a－2>2，解得a>，

当1≤a<2时，a－1＋2－a>2，不等式无解，

当a≤1时，1－a＋2－a>2，解得a<，

综上所述，a的取值范围为∪.

(2)因为f(x)<b，所以|x－a|＋x<b，

当x≥a时，x－a＋x<b，得x<，

当x<a时，a－x＋x<b，得a<b，

因为不等式f(x)<b的解集为，则

又因为a，b∈N*，所以a＝1，b＝2.

考向二　绝对值三角不等式的应用

例2　(1)(2019·漳州二模)已知f(x)＝|x＋a|(a∈R)．

①若f(x)≥|2x－1|的解集为[0,2]，求a的值；

②若对任意x∈R，不等式f(x)＋|x－a|≥3a－2恒成立，求实数a的取值范围．

解　①不等式f(x)≥|2x－1|，即|x＋a|≥|2x－1|，

两边平方整理，得3x2－(2a＋4)x＋1－a2≤0，

由题意，知0和2是方程3x2－(2a＋4)x＋1－a2＝0的两个实数根，

即解得a＝1.

②因为f(x)＋|x－a|＝|x＋a|＋|x－a|≥|(x＋a)－(x－a)|＝2|a|，

所以要使不等式f(x)＋|x－a|≥3a－2恒成立，只需2|a|≥3a－2，

当a≥0时，2a≥3a－2，解得a≤2，即0≤a≤2；

当a<0时，－2a≥3a－2，解得a≤，即a<0.

综上所述，实数a的取值范围是(－∞，2]．

(2)(2019·长沙一模)已知函数f(x)＝x|x－a|，a∈R.

①当f(1)＋f(－1)>1时，求实数a的取值范围；

②若a>0，∀x，y∈(－∞，a]，不等式f(x)≤|y＋|＋|y－a|恒成立，求实数a的取值范围．

解　①f(1)＋f(－1)＝|1－a|－|1＋a|>1，

若a≤－1，则1－a＋1＋a>1，得2>1，即a≤－1；

若－1<a<1，则1－a－(1＋a)>1，得a<－，

即－1<a<－；

若a≥1，则－(1－a)－(1＋a)>1，得－2>1，此时不等式无解．

综上所述，实数a的取值范围是.

②由题意，知要使不等式恒成立，

只需f(x)max≤min.

当x∈(－∞，a]时，f(x)＝－x2＋ax，f(x)max＝f＝.

因为|y＋|＋|y－a|≥|a＋|，当且仅当·(y－a)≤0，即－≤y≤a时等号成立，

所以当y∈(－∞，a]时，

min＝|a＋|＝a＋.

于是≤a＋，解得－1≤a≤5.

又a>0，所以实数a的取值范围是(0,5]．

两数和与差的绝对值不等式的性质

(1)对绝对值三角不等式定理|a|－|b|≤|a±b|≤|a|＋|b|中等号成立的条件要深刻理解，特别是用此定理求函数的最值时．

(2)该定理可强化为||a|－|b||≤|a±b|≤|a|＋|b|，它经常用于证明含绝对值的不等式．

[即时训练]　3.(2019·江西上饶模拟)已知函数f(x)＝|2x＋a|＋|2x－1|，g(x)＝|x－1|＋2.

(1)解不等式g(x)≥4；

(2)若对任意x2∈R，都有x1∈R，使得f(x1)＝g(x2)成立，求实数a的取值范围．

解　(1)由|x－1|＋2≥4，得|x－1|≥2，

解得x≤－1或x≥3.

故不等式g(x)≥4的解集为{x|x≤－1或x≥3}．

(2)因为对任意x2∈R，都有x1∈R，使得f(x1)＝g(x2)成立，所以{y|y＝g(x)}⊆{y|y＝f(x)}．

又因为g(x)＝|x－1|＋2≥2，f(x)＝|2x＋a|＋|2x－1|≥|(2x＋a)－(2x－1)|＝|a＋1|，

所以|a＋1|≤2，解得－3≤a≤1，

所以实数a的取值范围为[－3,1]．

4．(2019·湖南怀化质检)设f(x)＝|2x－1|＋|x＋1|.

(1)解不等式f(x)≤3；

(2)若不等式m|x|≤f(x)恒成立，求m的取值范围．

解　(1)当x<－1时，f(x)＝－(2x－1)－(x＋1)＝－3x≤3，解得x≥－1，故此情况无解；

当－1≤x≤时，f(x)＝－(2x－1)＋(x＋1)＝－x＋2≤3，解得x≥－1，故－1≤x≤；

当x>时，f(x)＝(2x－1)＋(x＋1)＝3x≤3，解得x≤1，故<x≤1.

综上所述，满足f(x)≤3的解集为{x|－1≤x≤1}．

(2)当x＝0时，可知∀m∈R，不等式均成立；

当x≠0时，由已知可得m≤恒成立，即m≤的最小值．

＝＝|2－|＋|1＋|≥|＋|＝3，当x≤－1或x≥时，等号成立，所以m≤3.

综上所述，使得不等式m|x|≤f(x)恒成立的m的取值范围为(－∞，3]．

考向三　绝对值不等式的综合应用

例3　(1)已知函数f(x)＝|x－2|＋|2x－1|.

①求不等式f(x)≤3的解集；

②若不等式f(x)≤ax的解集为空集，求实数a的取值范围．

解　①解法一：由题意f(x)＝

当x≤时，f(x)＝－3x＋3≤3，解得x≥0，即0≤x≤，

当<x<2时，f(x)＝x＋1≤3，解得x≤2，即<x<2，

当x≥2时，f(x)＝3x－3≤3，解得x≤2，即x＝2.

综上所述，原不等式的解集为[0,2]．

解法二：由题意

f(x)＝

作出f(x)的图象，如图．

注意到当x＝0或x＝2时，f(x)＝3，

结合图象，知不等式f(x)≤3的解集为[0,2]，

②解法一：不等式f(x)≤ax的解集为空集可转化为f(x)>ax对任意x∈R恒成立，即函数y＝ax的图象始终在函数y＝f(x)的图象的下方，如图．

当直线y＝ax过点A(2,3)以及与直线y＝－3x＋3平行时为临界点，所以－3≤a<.

解法二：不等式f(x)≤ax的解集为空集可转化为f(x)>ax对任意x∈R恒成立，

(ⅰ)当x≤时，f(x)＝－3x＋3>ax，即(a＋3)x－3<0恒成立，

若a＋3<0，显然不符合题意，

若a＋3＝0，即a＝－3，则－3<0恒成立，符合题意，

若a＋3>0，即a>－3，只需(a＋3)×－3<0即可，解得a<3，故－3<a<3，所以－3≤a<3；

(ⅱ)当<x<2时，f(x)＝x＋1>ax，即(a－1)x－1<0恒成立，

若a－1<0，即a<1，(a－1)x－1<0恒成立，符合题意，

若a－1＝0，即a＝1，则－1<0恒成立，符合题意，

若a－1>0，即a>1，只需(a－1)×2－1≤0即可，

解得a≤，故1<a≤，所以a≤；

(ⅲ)当x≥2时，f(x)＝3x－3>ax，即(a－3)x＋3<0恒成立，

若a－3<0，即a<3，只需(a－3)×2＋3<0即可，

解得a<，故a<，

若a－3＝0，即a＝3，则3<0，不符合题意，

若a－3>0，即a>3，则(a－3)x＋3>0恒成立，不符合题意，所以a<.

综上所述，－3≤a＜.

(2)(2019·郑州二模)设函数f(x)＝|ax＋1|＋|x－a|(a>0)，g(x)＝x2－x.

①当a＝1时，求不等式g(x)≥f(x)的解集；

②已知f(x)≥2恒成立，求实数a的取值范围．

解　①当a＝1时，

f(x)＝|x＋1|＋|x－1|＝

当x≤－1时，x2－x≥－2x，得x≤－1；

当－1<x<1时，x2－x≥2，即x≤－1或x≥2，舍去；

当x≥1时，x2－x≥2x，得x≥3.

综上，原不等式的解集为{x|x≤－1或x≥3}．

②f(x)＝|ax＋1|＋|x－a|

＝

当0<a≤1时，f(x)min＝f(a)＝a2＋1≥2，得a＝1；

当a>1时，f(x)min＝f＝a＋≥2，得a>1.

综上，实数a的取值范围为[1，＋∞)．

(1)解决与绝对值有关的综合问题的关键是去掉绝对值，化为分段函数来解决．

(2)数形结合是解决与绝对值有关的综合问题的常用方法．

[即时训练]　5.(2019·宁德模拟)已知f(x)＝|2x－1|＋|ax－5|(0<a<5)．

(1)当a＝1时，求不等式f(x)≥9的解集；

(2)若函数y＝f(x)的最小值为4，求实数a的值．

解　(1)当a＝1时，

f(x)＝|2x－1|＋|x－5|＝

所以f(x)≥9⇔或

或解得x≤－1或x≥5，

即所求不等式的解集为(－∞，－1]∪[5，＋∞)．

(2)∵0<a<5，∴>1，

则f(x)＝

注意到当x<时，f(x)单调递减，当x>时，f(x)单调递增，

∴f(x)的最小值在上取得，

∵在上，当0<a<2时，f(x)单调递增；当a＝2时，f(x)＝4；当2<a<5时，f(x)单调递减，

∴或

解得a＝2.

6．(2019·广州二模)已知函数f(x)＝|2x－1|－a.

(1)当a＝1时，解不等式f(x)＞x＋1；

(2)若存在实数x，使得f(x)＜f(x＋1)成立，求实数a的取值范围．

解　(1)当a＝1时，由f(x)＞x＋1，得|2x－1|－1＞x＋1.

当x≥时，2x－1－1＞x＋1，解得x＞3.

当x＜时，1－2x－1＞x＋1，解得x＜－.

综上可知，不等式f(x)＞x＋1的解集为.

(2)由f(x)<f(x＋1)，得|2x－1|－a<|2x＋1|－.则a>2|2x－1|－|2x＋1|，

令g(x)＝2|2x－1|－|2x＋1|，

则问题等价于a>g(x)min.

因为||2x－1|－|2x＋1||≤|(2x－1)－(2x＋1)|＝2，

即－2≤|2x－1|－|2x＋1|≤2，则|2x－1|－|2x＋1|≥－2.

所以g(x)＝|2x－1|－|2x＋1|＋|2x－1|≥－2＋|2x－1|≥－2，

当且仅当x＝时等号成立．所以g(x)min＝－2.

所以实数a的取值范围为(－2，＋∞)．