所属成套资源：人教版八上全等三角形同步培优+单元测试

成套系列资料，整套一键下载

浏览整套资料 (共13份)

数学12.2 三角形全等的判定导学案

展开

这是一份数学12.2 三角形全等的判定导学案，共7页。
全等三角形-全等三角形的判定

、选择题

LISTNUM OutlineDefault \l 3 如图，AB=CD，AB∥CD，判定△ABC≌△CDA的依据是( )

A.SSS B.SAS C.ASA D.HL

LISTNUM OutlineDefault \l 3 如图，△ABC和△DEF中，AB=DE、∠B=∠DEF，添加下列哪一个条件无法证明△ABC≌△DEF（）

A.AC∥DF B.∠A=∠D C.AC=DF D.∠ACB=∠F

LISTNUM OutlineDefault \l 3 如图，已知∠ABC=∠BAD，添加下列条件还不能判定△ABC≌△BAD的是（）

A．AC=BD B．∠CAB=∠DBA C．∠C=∠D D．BC=AD

LISTNUM OutlineDefault \l 3 如图．从下列四个条件：

①BC=B′C，②AC=A′C，③∠A′CA=∠B′CB，④AB=A′B′中，

任取三个为条件，余下的一个为结论，则最多可以构成正确的结论的个数是（）

A．1个 B．2个 C．3个 D．4个

LISTNUM OutlineDefault \l 3 在△ABC和△FED中，已知∠C=∠D，∠B=∠E，要判定这两个三角形全等，还需要条件（）

A．AB=EDB．AB=FDC．AC=FDD．∠A=∠F

LISTNUM OutlineDefault \l 3 下列判断中错误的是（）

A．有两角和一边对应相等的两个三角形全等

B．有两边和一角对应相等的两个三角形全等

C．有两边和其中一边上的中线对应相等的两个三角形全等

D．有一边对应相等的两个等边三角形全等

LISTNUM OutlineDefault \l 3 平面上有△ACD与△BCE，其中AD与BE相交于P点，如图．若AC=BC，AD=BE，CD=CE，∠ACE=55°，∠BCD=155°，则∠BPD的度数为（）

A．110° B．125° C．130° D．155°

LISTNUM OutlineDefault \l 3 某同学把一块三角形的玻璃打碎了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的方法是（）

A．带①去 B．带②去 C．带③去 D．带①②③去

LISTNUM OutlineDefault \l 3 如图，在四边形ABCD中，AB=AD，CB=CD，若连接AC、BD相交于点O，则图中全等三角形共有（）

A.1对 B.2对 C.3对 D.4对

LISTNUM OutlineDefault \l 3 如图，已知在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD，BE.

以下四个结论：

①BD=CE；②∠ACE+∠DBC=45°；③BD⊥CE；④∠BAE+∠DAC=180°.

其中结论正确的个数是（）

A.1 B.2 C.3 D.4

、填空题

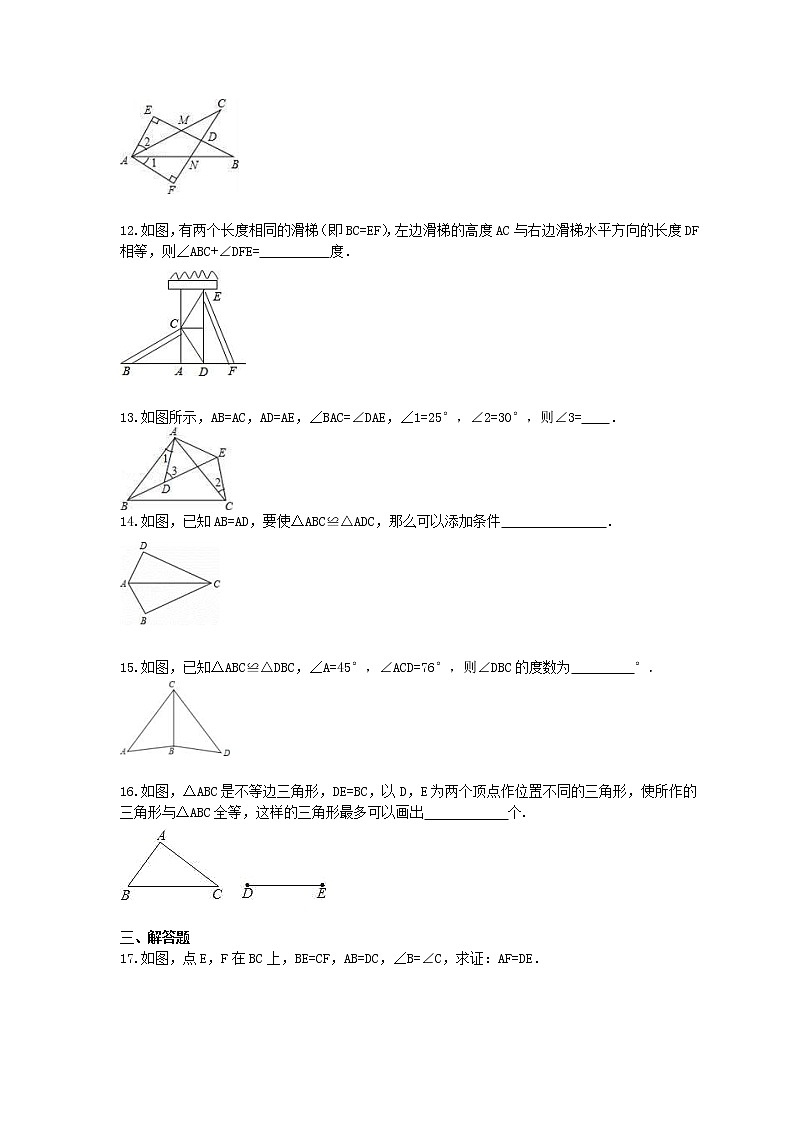
LISTNUM OutlineDefault \l 3 如图EB交AC于M，交FC于D，AB交FC于N，∠E=∠F=90°，∠B=∠C，AE=AF．给出下列结论：①∠1=∠2；②BE=CF；③△ACN≌△ABM；④CD=DN．其中正确的结论有（填序号）．

LISTNUM OutlineDefault \l 3 如图，有两个长度相同的滑梯（即BC=EF），左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，则∠ABC+∠DFE= 度．

LISTNUM OutlineDefault \l 3 如图所示，AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3= ．

LISTNUM OutlineDefault \l 3 如图，已知AB=AD，要使△ABC≌△ADC，那么可以添加条件．

LISTNUM OutlineDefault \l 3 如图，已知△ABC≌△DBC，∠A=45°，∠ACD=76°，则∠DBC的度数为 °．

LISTNUM OutlineDefault \l 3 如图，△ABC是不等边三角形，DE=BC，以D，E为两个顶点作位置不同的三角形，使所作的三角形与△ABC全等，这样的三角形最多可以画出个.

、解答题

LISTNUM OutlineDefault \l 3 如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C，求证：AF=DE．

LISTNUM OutlineDefault \l 3 如图，AB=AD，BC=DC，点E在AC上．

(1)求证：AC平分∠BAD；

(2)求证：BE=DE．

LISTNUM OutlineDefault \l 3 如图，AE和BD相交于点C，∠A=∠E，AC=EC．求证：△ABC≌△EDC．

LISTNUM OutlineDefault \l 3 已知△ABN和△ACM位置如图所示，AB=AC，∠1=∠2，∠M=∠N．求证：AD=AE．

LISTNUM OutlineDefault \l 3 如图，在△ABD和△ACE中，有四个等式：①AB=AC；②AD=AE；③∠1=∠2；④BD=CE，请你从其中三个等式作为题设，设另一个作为结论，写出一个真命题，并给出证明.（要求写出已知、求证及证明过程）

LISTNUM OutlineDefault \l 3 如图所示，已知AE⊥AB，AF⊥AC，AE=AB，AF=AC.

求证：（1）EC=BF；

（2）EC⊥BF.

参考答案

LISTNUM OutlineDefault \l 3 \s 1 B.

LISTNUM OutlineDefault \l 3 C．

LISTNUM OutlineDefault \l 3 A

LISTNUM OutlineDefault \l 3 B

LISTNUM OutlineDefault \l 3 C

LISTNUM OutlineDefault \l 3 B

LISTNUM OutlineDefault \l 3 C

LISTNUM OutlineDefault \l 3 C

LISTNUM OutlineDefault \l 3 答案为：C.

LISTNUM OutlineDefault \l 3 D

LISTNUM OutlineDefault \l 3 答案为：①②③．

LISTNUM OutlineDefault \l 3 答案为：90．

LISTNUM OutlineDefault \l 3 答案为：55°．

LISTNUM OutlineDefault \l 3 答案为：DC=BC(或∠DAC=∠BAC或AC平分∠DAB等)

LISTNUM OutlineDefault \l 3 答案为：97．

LISTNUM OutlineDefault \l 3 答案为：4.

LISTNUM OutlineDefault \l 3 证明：∵BE=CF，∴BE+EF=CF+EF，即BF=CE，

在△ABF和△DCE中，，

∴△ABF≌△DCE(SAS)

∴AF=DE．

LISTNUM OutlineDefault \l 3 解：

(1)在△ABC与△ADC中，

∴△ABC≌△ADC(SSS)

∴∠BAC=∠DAC即AC平分∠BAD；

(2)由(1)∠BAE=∠DAE

在△BAE与△DAE中，得

∴△BAE≌△DAE(SAS)

∴BE=DE

LISTNUM OutlineDefault \l 3 证明：

∵在△ABC和△EDC中，

，

∴△ABC≌△EDC（ASA）．

LISTNUM OutlineDefault \l 3 证明：∵∠M=∠N，

∴∠MDO=∠NEO，

∴∠BDA=∠CEA，

∴在△ABD和△ACE中，

∵ ，

∴△ABD≌△ACE（AAS），

∴AD=AE．

LISTNUM OutlineDefault \l 3 解：如果AB=AC，AD=AE，BD=CE，那么∠1=∠2.

已知：在△ABD和△ACE中，AB=AC，AD=AE，BD=CE，

求证：∠1=∠2.

证明：在△ABD和△ACE中，，∴△ABD≌△ACE，

∴∠BAD=∠CAE，∴∠1=∠2.

LISTNUM OutlineDefault \l 3 证明：（1）∵AE⊥AB，AF⊥AC，

∴∠BAE=∠CAF=90°，

∴∠BAE+∠BAC=∠CAF+∠BAC，

即∠EAC=∠BAF，

在△ABF和△AEC中，

∵，

∴△ABF≌△AEC（SAS），

∴EC=BF；

（2）如图，根据（1），△ABF≌△AEC，

∴∠AEC=∠ABF，

∵AE⊥AB，∴∠BAE=90°，

∴∠AEC+∠ADE=90°，

∵∠ADE=∠BDM（对顶角相等），

∴∠ABF+∠BDM=90°，

在△BDM中，∠BMD=180°﹣∠ABF﹣∠BDM=180°﹣90°=90°，

所以EC⊥BF.