





北师大版 (2019)4.2 简单幂函数的图像和性质优质ppt课件
展开幂函数在生活、建筑、军事等多个领域都有着重要的应用.那么幂函数如何定义?它的图象和性质是怎样的呢?
一、幂函数的定义一般地,形如 (α为常数)的函数,即 是自变量、 是常数的函数称为幂函数. 名师点析1.幂的指数是一个常数,它可以取任意实数;2.幂值前面的系数是1,否则不是幂函数,如函数y=5 就不是幂函数.3.幂函数的定义域是使xα有意义的所有x的集合,因α的不同,定义域也不同.
微练习在函数①y= ,②y=3x2,③y=x2+2x中,幂函数的序号为 .(填序号)
答案:① 解析:函数y= =x-4为幂函数;函数y=3x2中x2的系数不是1,所以它不是幂函数;函数y=x2+2x不是y=xα(α∈R)的形式,所以它不是幂函数.
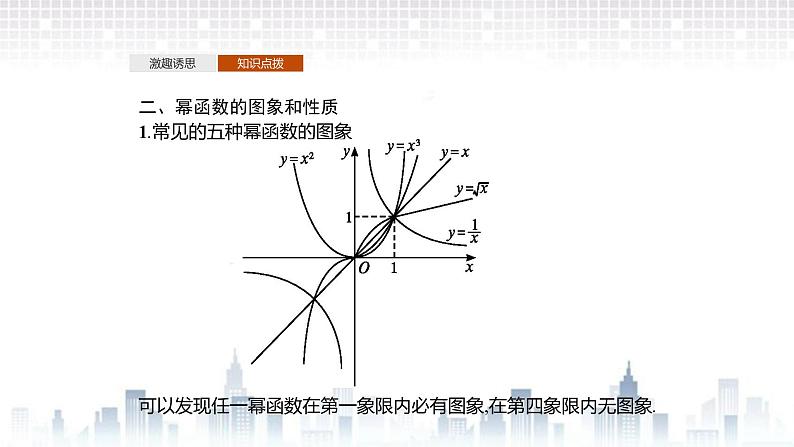
二、幂函数的图象和性质1.常见的五种幂函数的图象
可以发现任一幂函数在第一象限内必有图象,在第四象限内无图象.
既不是奇函数,也不是偶函数
名师点析幂函数y=xα的上述性质可归纳如下:(1)当α>0时,图象都通过点(0,0),(1,1);在第一象限内,函数单调递增.(2)当α<0时,图象都通过点(1,1);在第一象限内,函数单调递减,图象向上与y轴无限接近,向右与x轴无限接近.
微判断判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.(1)幂函数的图象可以出现在平面直角坐标系中的任意一个象限.( )(2)幂函数的图象必过(0,0)和(1,1).( )
答案: (1)× (2)×
(2)已知幂函数f(x)=xα的图象经过点(2, ),则函数f(x)为( )A.奇函数且在(0,+∞)上单调递增B.偶函数且在(0,+∞)上单调递减C.既不是奇函数,又不是偶函数且在(0,+∞)上单调递增D.既不是奇函数,又不是偶函数且在(0,+∞)上单调递减
答案: (1) C (2) C
幂函数的概念例1函数f(x)=(m2-m-5)xm-1是幂函数,且当x∈(0,+∞)时,f(x)单调递增,试确定m的值.分析由f(x)=(m2-m-5)xm-1是幂函数,且当x>0时单调递增,可先利用幂函数的定义求出m的值,再利用单调性确定m的值.
解:根据幂函数的定义,得m2-m-5=1,解得m=3或m=-2.当m=3时,f(x)=x2在(0,+∞)上单调递增;当m=-2时,f(x)=x-3在(0,+∞)上单调递减,不符合要求.故m=3.
反思感悟判断一个函数是否为幂函数的依据是该函数是否为y=xα(α为常数)的形式,即:(1)系数为1;(2)指数为常数;(3)后面不加任何项.反之,若一个函数为幂函数,则该函数必具有这种形式.
变式训练1如果幂函数y=(m2-3m+3) 的图象不过原点,求实数m的取值.
解:由幂函数的定义得m2-3m+3=1,解得m=1或m=2;当m=1时,m2-m-2=-2,函数为y=x-2,其图象不过原点,满足条件;当m=2时,m2-m-2=0,函数为y=x0,其图象不过原点,满足条件.综上所述,m=1或m=2.
幂函数的图象例2已知函数y=xa,y=xb,y=xc的图象如图所示,则a,b,c的大小关系为( )A.c
答案:A 解析:由幂函数的图象特征,知c<0,a>1,0
变式训练2如图所示,曲线C1与C2分别是函数y=xm和y=xn在第一象限内的图象,则下列结论正确的是( )A.n
答案:A 解析:画出直线y=x0的图象,作出直线x=2,与三个函数图象交于点(2,20),(2,2m),(2,2n).由三个点的位置关系可知,n
反思感悟1.比较幂大小的三种常用方法
2.利用幂函数单调性比较大小时要注意的问题比较大小的两个实数必须在同一函数的同一个单调区间内,否则无法比较大小.
A.b
解:根据幂函数y=x1.3的图象,知当0
幂函数的“凸”性(1)上凸函数、下凸函数的定义
(2)幂函数的凸性①幂函数y=xα,x∈(0,+∞),在α>1时,函数是下凸函数;②幂函数y=xα,x∈(0,+∞),在0<α<1时,函数是上凸函数;③幂函数y=xα,x∈(0,+∞),在α<0时,函数是下凸函数.
这个定义从几何形式上看就是:在函数f(x)的图象上取任意两点,如果函数图象在这两点之间的部分总在连接这两点的线段的上方,那么这个函数就是上凸函数;如果函数图象在这两点之间的部分总在连接这两点的线段的下方,那么这个函数就是下凸函数.根据函数图象判断,一般开口向下的二次函数是上凸函数,开口向上的二次函数是下凸函数.
典例如图,fi(x)(i=1,2,3,4)是定义在区间[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的x1和x2,任意λ∈[0,1],f[λx1+(1-λ)x2]≤λf(x1)+(1-λ)f(x2)恒成立”的只有( )
A.f1(x) B.f2(x)C.f3(x)D.f4(x)
再结合函数f(x)图象的凹凸性,可排除B,C,D三个选项,正确答案为A.
1.幂函数y=kxα过点(4,2),则k-α的值为( )
答案:B 解析:幂函数y=kxα过点(4,2),
A.C2,C1,C3,C4B.C4,C1,C3,C2C.C3,C2,C1,C4D.C1,C4,C2,C3
3.幂函数f(x)=x3m-5(m∈N)在区间(0,+∞)上是单调递减,且对定义域中的任意x,有f(-x)=f(x),则m等于( )A.0B.1C.2D.3
答案:B 解析:幂函数f(x)=x3m-5(m∈N)在(0,+∞)上单调递减,则3m-5<0,即
又m∈N,故m=0或m=1.∵f(-x)=f(x),∴f(x)是偶函数.当m=0时,f(x)=x-5是奇函数;当m=1时,f(x)=x-2是偶函数,符合题意.
北师大版 (2019)必修 第一册4.1 函数的奇偶性教案配套ppt课件: 这是一份北师大版 (2019)必修 第一册4.1 函数的奇偶性教案配套ppt课件,共34页。PPT课件主要包含了目录索引,本节要点归纳等内容,欢迎下载使用。
数学必修 第一册4.1 函数的奇偶性授课课件ppt: 这是一份数学必修 第一册4.1 函数的奇偶性授课课件ppt,共46页。PPT课件主要包含了必备知识•探新知,基础知识,知识点1,知识点2,xx≠0,0+∞,非奇非偶,-∞0,基础自测,关键能力•攻重难等内容,欢迎下载使用。
北师大版 (2019)必修 第一册4.2 简单幂函数的图像和性质教学ppt课件: 这是一份北师大版 (2019)必修 第一册4.2 简单幂函数的图像和性质教学ppt课件













