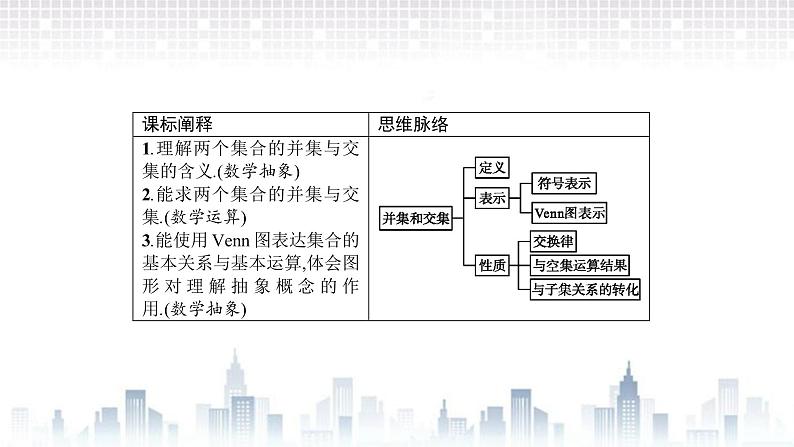
北师大版 (2019)必修 第一册1.3 集合的基本运算完美版课件ppt

这是一份北师大版 (2019)必修 第一册1.3 集合的基本运算完美版课件ppt，共34页。PPT课件主要包含了第1课时交集和并集，激趣诱思，知识点拨，探究一，探究二，探究三，素养形成，当堂检测，则A∪BR，答案5或-3等内容，欢迎下载使用。

公务员,是指在各级政府机关中,行使国家行政职权,执行国家公务的人员.每年都有很多人报名参加考试,常出现一个岗位若干人争夺的局面.2020国家公务员考试报考条件中规定,报考人员应符合以下条件(摘录):(1)具有中华人民共和国国籍;(2)18周岁以上、35周岁以下(1983年10月至2001年10月期间出生),2020年应届硕士研究生和博士研究生(非在职)人员年龄可放宽到40周岁以下(1978年10月以后出生);……(7)具有大学专科及以上文化程度.根据以上条件,哪些人可以报名参加公务员考试呢?
名师点析求两个集合的交集,结果还是一个集合,是由集合A与B的所有公共元素组成的集合.当两个集合没有公共元素时,两个集合的交集是空集,而不能说两个集合没有交集.
{x|x∈A,且x∈B}
微练习(1)已知集合A={1,3,5,6,7},B={2,4,5,6,8},则A∩B=　　　　　. (2)(2019全国Ⅱ)已知集合A={x|x>-1},B={x|x<2},则A∩B=(　　)A.(-1,+∞)　　　B.(-∞,2)C.(-1,2) D.⌀
(3)已知集合A={-1,0,1,2,3},B={x|-2≤x≤2},那么A∩B=(　　)A.{-1,0,1}B.{-1,0,1,2}C.{-1,0,1,2,3}D.{x|-2≤x≤2}
答案: (1){5,6}　(2) C　 (3)B
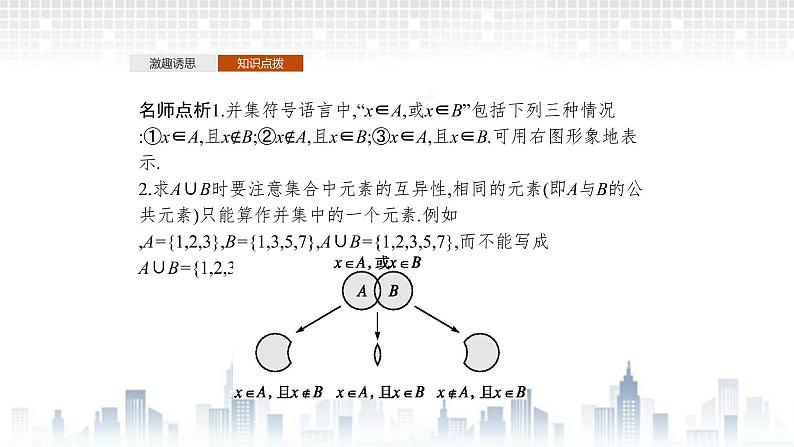
名师点析1.并集符号语言中,“x∈A,或x∈B”包括下列三种情况:①x∈A,且x∉B;②x∉A,且x∈B;③x∈A,且x∈B.可用右图形象地表示.2.求A∪B时要注意集合中元素的互异性,相同的元素(即A与B的公共元素)只能算作并集中的一个元素.例如,A={1,2,3},B={1,3,5,7},A∪B={1,2,3,5,7},而不能写成A∪B={1,2,3,1,3,5,7}.
微练习(1)设集合A={1,3},集合B={1,2,4,5},则集合A∪B=(　　)A.{1,3,1,2,4,5}B.{1}C.{1,2,3,4,5}D.{2,3,4,5}(2)已知集合A={x|x>-2},B={x|x≥1},则A∪B=(　　)A.{x|x>-2} B.{x|-2答案: (1) C　(2)A　(3)2
集合的交集与并集运算例1(1)设集合A={x|x2-2x-3=0},B={x|x2=1},则A∪B=(　　)A.{1} B.{1,3} C.{-1,1,3}D.{-1,1}(2)已知集合A={x|x<2},B={x≥1},则A∪B=(　　)A.{x|x<2}B.{x|1≤x<2}C.{x|x≥1}D.R分析(1)先解一元二次方程得集合A,B,再根据集合并集的定义求结果;(2)用数轴表示集合A,B,根据定义求解.
解析:(1)A={-1,3},B={-1,1},A∪B={-1,1,3}.(2)在数轴上表示出集合A,B,则
答案: (1) C　(2)D　
变式训练1(1)已知集合A={x∈N|1≤x≤3},B={2,3,4,5},则A∪B=(　　)A.{2,3}B.{2,3,4,5}C.{2}D.{1,2,3,4,5}(2)设集合A={x∈N+|x≤2},B={2,6},则A∪B=(　　)A.{2} B.{2,6}C.{1,2,6}D.{0,1,2,6}
答案: (1) D　(2)C
例2(1)已知集合A={1,3,5,7},B={2,3,4,5},则A∩B=(　　)A.{3}B.{5}C.{3,5}D.{1,2,3,4,5,7}(2)设集合M={x|-3答案: (1) C　(2) A　(3) D　
解析:(1)直接由交集定义可得A∩B={3,5};(2)在数轴上表示集合M,N,如图:
∴M∩N={x|1≤x<2}.(3)A∩C={1,2},(A∩C)∪B={1,2,3,4},故选D.
反思感悟 求两个集合交集、并集的方法技巧当求两个集合的并集、交集时,对于用描述法给出的集合,首先明确集合中的元素,其次将两个集合化为最简形式;对于连续的数集常借助于数轴写出结果,此时要注意数轴上方所有“线”下面的实数组成了并集,数轴上方“双线”(即公共部分)下面的实数组成了交集,此时要注意当端点不在集合中时,应用空心点表示;对于用列举法给出的集合,则依据并集、交集的含义,可直接观察或借助于Venn图写出结果.
变式训练2若集合M={x∈R|-3答案:B　解析:N={-1,0,1,2},M={x∈R|-3已知集合的交集、并集求参数例3已知a∈R,集合A={-4,2a-1,a2},B={a-5,1-a,9}.若9∈A∩B,则实数a的值为　　　　　. 分析9∈A∩B说明9∈A,通过分类讨论建立关于a的方程求解,注意求出a的值后要代入集合A,B中,看是否满足集合中元素的互异性.
解析:∵9∈A∩B,∴9∈A,且9∈B,∴2a-1=9或a2=9,解得a=5或a=±3.当a=5时,A={-4,9,25},B={0,-4,9},符合题意;当a=3时,A={-4,5,9},B={-2,-2,9},集合B不满足集合中元素的互异性,故a≠3;当a=-3时,A={-4,-7,9},B={-8,4,9},符合题意.综上可得实数a的值为5或-3.
反思感悟 已知两个有限集运算结果求参数值的方法对于这类已知两个有限集的运算结果求参数值的问题,一般先用观察法得到不同集合中元素之间的关系,再列方程求解.另外,在处理有关含参数的集合问题时,要注意对求解结果进行检验,检验求解结果是否满足集合中元素的有关特性,尤其是互异性.
延伸探究例3中,将“9∈A∩B”改为“A∩B={9}”,其余条件不变,求实数a的值及A∪B.
解:∵A∩B={9},∴9∈A.∴2a-1=9或a2=9,解得a=5或a=±3.当a=5时,A={-4,9,25},B={0,-4,9},由于A∩B={-4,9},不符合题意,故a≠5;当a=3时,A={-4,5,9},B={-2,-2,9},集合不满足集合中元素的互异性,故a≠3;当a=-3时,A={-4,-7,9},B={-8,4,9},且A∩B={9},符合题意.综上可得a=-3.此时A∪B={-8,-4,-7,4,9}.
例4集合A={x|-1解:(1)A={x|-1∴数轴上点x=a在点x=-1左侧,且包含点x=-1,∴a的取值范围为a≤-1.(2)A={x|-1∴数轴上点x=a在点x=-1和点x=1之间,不包含点x=-1,但包含点x=1.∴a的取值范围为-1反思感悟 已知集合运算求参数的思路此类问题常借助数轴解决,首先根据集合间的关系画出数轴,然后根据数轴列出关于参数的不等式(组)求解,特别要注意端点值的取舍.当集合的元素离散时,常借助集合的关系列关于参数的方程(组)求解,但求解后要代入检验是否符合题意.
延伸探究例4(1)中,把“A∩B=⌀”改为“A∩B≠⌀”,求a的取值范围.
解:利用数轴(略)表示出两个集合,数形结合知,要使A∩B≠⌀,需数轴上点x=a在点x=-1右侧且不包含点x=-1,所以a的取值范围为a>-1.
集合的交集、并集性质的应用例5设集合M={x|-2综上可知,实数t的取值范围是{t|t≤2}.
答案:{t|t≤2}
延伸探究将例5条件中“M∪N=M”改为“M∩N=M”,其余不变,求实数t的取值范围.
解:由M∩N=M,得M⊆N,故N≠⌀.用数轴(略)表示两个集合,
故实数t的取值范围为t≥4.
例6设集合A={x|x2-2x=0},B={x|x2-2ax+a2-a=0}.(1)若A∩B=B,求a的取值范围;(2)若A∪B=B,求a的值.分析先化简集合A,B,再由已知条件得A∩B=B和A∪B=B,转化为集合A,B的包含关系,分类讨论求a的值或取值范围.
解:由x2-2x=0,得x=0或x=2.∴A={0,2}.(1)∵A∩B=B,∴B⊆A,B=⌀,{0},{2},{0,2}.当B=⌀时,Δ=4a2-4(a2-a)=4a<0,∴a<0;
综上所述,得a的取值范围是{a|a=1或a≤0}.(2)∵A∪B=B,∴A⊆B.∵A={0,2},而B中方程至多有两个根,∴A=B,由(1)知a=1.
反思感悟 利用交集、并集运算求参数的思路(1)涉及A∩B=B或A∪B=A的问题,可利用集合的运算性质,转化为相关集合之间的关系求解,要注意空集的特殊性.(2)将集合中的运算关系转化为两个集合之间的关系.若集合中的元素能一一列举,则可用观察法得到不同集合中元素之间的关系,要注意集合中元素的互异性;与不等式有关的集合,则可利用数轴得到不同集合之间的关系.
变式训练3已知集合M={x|2x-4=0},集合N={x|x2-3x+m=0},(1)当m=2时,求M∩N,M∪N;(2)当M∩N=M时,求实数m的值.
解:(1)由题意得M={2}.当m=2时,N={x|x2-3x+2=0}={1,2},∴M∩N={2},M∪N={1,2}.(2)∵M∩N=M,∴M⊆N.∵M={2},∴2∈N,∴2是关于x的方程x2-3x+m=0的解,即4-6+m=0,解得m=2.
分类讨论思想在集合运算中的应用分类讨论就是分别归类再进行讨论的意思,数学中的分类过程就是对事件共性的抽象过程.解题时要明确为什么分类,如何分类,如何确定分类的标准.应用时,首先要审清题意,认真分析可能产生的不同因素.进行讨论时要确定分类的标准,每一次分类只能按照一个标准来分,不能重复也不能遗漏.
典例 设集合A={x|x2-3x+2=0},B={x|x2+2(a+1)x+a2-5=0}.(1)若A∩B={2},求实数a的值;(2)若A∪B=A,求实数a的取值范围.解:(1)集合A={x|x2-3x+2=0}={1,2},若A∩B={2},则x=2是方程x2+2(a+1)x+a2-5=0的实数根,可得a2+4a+3=0,解得a=-3或a=-1.当a=-3时,B={2};当a=-1时,B={-2,2},均满足A∩B={2}.综上,实数a的值为a=-3或a=-1.(2)A={x|x2-3x+2=0}={1,2},B={x|x2+2(a+1)x+(a2-5)=0},对应的Δ=4(a+1)2-4(a2-5)=8(a+3).∵A∪B=A,∴B⊆A.
①当Δ<0,即a<-3时,B=⌀,满足条件;②当Δ=0,即a=-3时,B={2},满足条件;③当Δ>0,即a>-3时,只有B={1,2},才能满足条件,由一元二次方程根与系数的关系,得1+2=-2(a+1),且1×2=a2-5.
方法点睛 将条件转化为两个集合的包含关系,因为集合B是由含参的一元二次方程的解组成的,所以应按其解的个数分类讨论.尤其不要忽略无解的情况,即B为空集的情况.
1.设集合A={x∈N+|-1≤x≤2},B={2,3},则A∪B=(　　)A.{-1,0,1,2,3}B.{1,2,3}C.[-1,2] D.[-1,3]
答案:B　解析:集合A={1,2},B={2,3},则A∪B={1,2,3}.
2.已知集合A={x|-33.已知集合A={0,1},B={a-2,2}.若A∩B={1},则A∪B=(　　)A.{0,1,2}B.{1}C.{0,1,2,3}D.{1,2}
答案:A　解析:由A∩B={1},得1=a-2,所以a=3.则B={1,2}.所以A∪B={0,1,2}.
4.已知集合A={0,1,2,8},B={-1,1,6,8},那么A∩B=　　　　　.