

北师大版 (2019)必修 第一册2.1 实际问题的函数刻画优质教学设计
展开§2 实际问题中的函数模型
2.1 实际问题的函数刻画
实际问题的函数刻画
(1)用函数刻画实际问题的条件:
在现实世界里,事物之间存在着广泛的联系,当面对的实际问题中存在几个变量,并且它们之间具有依赖关系时,我们往往用函数对其进行刻画.
(2)用函数刻画实际问题的方法:
函数刻画的方法可以使用图象,但最多的还是使用解析式.
思考:世界上很多事物间的联系可以用函数刻画,在试图用函数刻画两个变量的联系时,需要关注哪些要点?
提示:先确定两个变量是谁;再看两个变量之间的对应关系是否满足函数定义;如果满足,就要考虑建立函数关系式.
1.下表是函数值y随自变量x变化的一组数据,它最可能的函数模型是( )
A.一次函数模型 B.幂函数模型
C.指数函数模型 D.对数函数模型
A [根据已知数据可知,自变量每增加1,函数值增加2,因此函数值的增量是均匀的,故为一次函数模型.]
2.某同学最近5年内的学习费用y(千元)与时间x(年)的关系如图所示,则可选择的模拟函数模型是( )
A.y=ax+b B.y=ax2+bx+c
C.y=aex+b D.y=a ln x+b
B [因为图中的点基本分布在一条抛物线上,所以可选择的函数模型应为二次函数,故选B.]
3.某同学从家里到学校,为了不迟到,先跑,跑累了再走余下的路,设在途中花的时间为t,离开家里的路程为d,下面图形中,能反映该同学的行程的是( )
A B C D
C [因为离开家里的路程为d越来越远,所以排除B和D,又该同学先跑后走,所以一开始速度大,离开家的距离d随着时间的增加增长的较快,所以选C.]
利用图象刻画实际问题
【例1】 (1)“龟兔赛跑”是一则经典故事:兔子与乌龟在赛道上赛跑,跑了一段后,兔子领先太多就躺在道边睡着了,当它醒来后看到乌龟已经领先了,因此它用更快地速度去追,结果还是乌龟先到了终点,请根据故事选出符合的路程—时间图象( )
A B C D
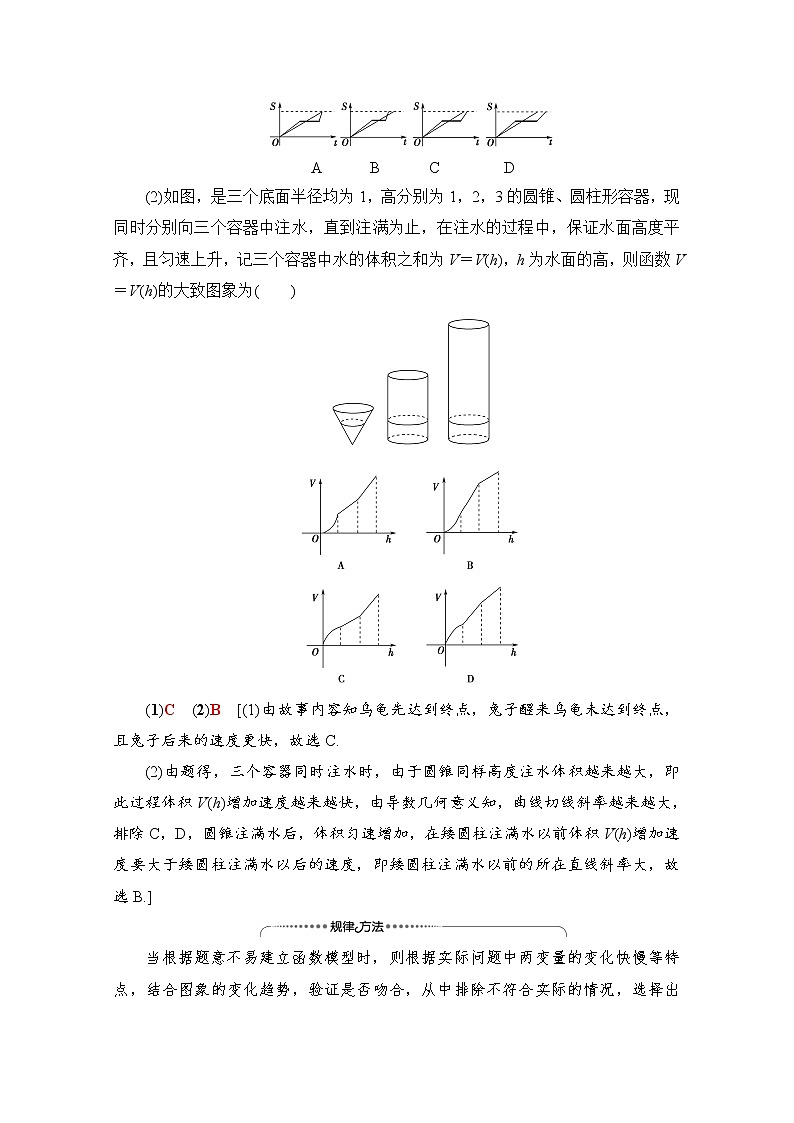
(2)如图,是三个底面半径均为1,高分别为1,2,3的圆锥、圆柱形容器,现同时分别向三个容器中注水,直到注满为止,在注水的过程中,保证水面高度平齐,且匀速上升,记三个容器中水的体积之和为V=V(h),h为水面的高,则函数V=V(h)的大致图象为( )
(1)C (2)B [(1)由故事内容知乌龟先达到终点,兔子醒来乌龟未达到终点,且兔子后来的速度更快,故选C.
(2)由题得,三个容器同时注水时,由于圆锥同样高度注水体积越来越大,即此过程体积V(h)增加速度越来越快,由导数几何意义知,曲线切线斜率越来越大,排除C,D,圆锥注满水后,体积匀速增加,在矮圆柱注满水以前体积V(h)增加速度要大于矮圆柱注满水以后的速度,即矮圆柱注满水以前的所在直线斜率大,故选B.]
当根据题意不易建立函数模型时,则根据实际问题中两变量的变化快慢等特点,结合图象的变化趋势,验证是否吻合,从中排除不符合实际的情况,选择出符合实际情况的答案.
eq \a\vs4\al([跟进训练])
1.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
A [通过题图可知A不正确,并不是逐月增加,但是每一年是递增的,所以B正确.从图观察C是正确的,D也正确,1~6月比较平稳,7~12月波动比较大.故选A.]
已知函数模型解决实际问题
[探究问题]
1.如何求形如y=x+ eq \f(a,x)(x>0,a>0)的函数的最小值?
提示:利用基本不等式a+b≥2 eq \r(ab).
2.如何求形如y=x+ eq \f(a,x+m)(x+m>0,a>0)的函数的最小值?
提示:利用换元法转化后用基本不等式求解.
【例2】 为了降低能源损耗,某体育馆的外墙需要建造隔热层,体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= eq \f(k,3x+5)(0≤x≤10,k为常数),若不建隔热层,每年能源消耗费用为8万元,设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值及f(x)的表达式;
(2)隔热层修建多厚时,总费用f(x)达到最小?并求最小值.
[思路点拨] eq \x(把x=0代入C(x))→ eq \x(求k的值)→ eq \x(函数f(x)的表达式)→ eq \x(f(x)的最小值)
[解] (1)当x=0时,C=8,∴k=40,∴C(x)= eq \f(40,3x+5)(0≤x≤10),
∴f(x)=6x+ eq \f(20×40,3x+5)=6x+ eq \f(800,3x+5)(0≤x≤10).
(2)由(1)得f(x)=2(3x+5)+ eq \f(800,3x+5)-10.
令3x+5=t,t∈[5,35],
则y=2t+ eq \f(800,t)-10≥2 eq \r(2t·\f(800,t))-10=70(当且仅当2t= eq \f(800,t),即t=20时等号成立),
此时x=5,因此f(x)的最小值为70.
∴隔热层修建5 cm厚时,总费用f(x)达到最小,最小值为70万元.
在例2(2)中,总费用f(x)有最大值吗?如果有,求出这个最大值;如果没有,说明理由.
[解] 由例2可知,f(x)=2(3x+5)+ eq \f(800,3x+5)-10.
令3x+5=t,t∈[5,35],设g(t)=2t+ eq \f(800,t)-10,
设t1,t2∈[5,35](t1>t2),则g(t1)-g(t2)=2t1+
eq \f(800,t1)-2t2- eq \f(800,t2)=2(t1-t2)× eq \f(t1t2-400,t1t2) ,
所以当t1,t2∈[5,20)时,g(t1)-g(t2)<0;
当t1,t2∈(20,35]时,g(t1)-g(t2)>0,
所以g(t)在[5,20)上单调递减,在(20,35]上单调递增,又g(5)=160,g(35)= eq \f(580,7),且160> eq \f(580,7),
所以当t=5时,g(t)的最大值为160,
即隔热层厚度为0 cm时,总费用f(x)达到最大值为160万元.
求解已给函数模型解决实际问题的关注点
(1)认清所给函数模型,弄清哪些量为待定系数.
(2)根据已知利用待定系数法,确定模型中的待定系数.
(3)利用该模型求解实际问题.
1.解应用题思路的关键是审题,不仅要明白、理解问题讲的是什么,还要特别注意一些关键的字眼(如“几年后”与“第几年后”,学生常常由于读题不谨慎而漏读和错读,导致题目不会做或函数解析式写错,故建议复习时务必养成良好的审题习惯.
2.在解应用题建模后一定要注意定义域,建模的关键是注意寻找量与量之间的相互依赖关系.
3.解决完数学模型后,注意转化为实际问题写出总结答案.
1.思考辨析(正确的画“√”,错误的画“×”)
(1)先有实际问题,后有模型.( )
(2)一个好的函数模型,既能与现有数据高度符合,又能很好地推演和预测.( )
(3)当自变量变化时,函数值的增长速度越来越快,那么该函数关系一定用指数函数模型来刻画.( )
[提示] (1)正确.
(2)正确.
(3)错误.也可能是用函数y=x2(x>0),y=x3等其它函数来刻画.
[答案] (1)√ (2)√ (3)×
2.如图是张大爷晨练时离家距离(y)与行走时间(x)之间的函数关系的图象.若用黑点表示张大爷家的位置,则张大爷散步行走的路线可能是( )
A B C D
D [由y与x的关系知,在中间时间段y值不变,只有D符合题意.]
3.“好酒也怕巷子深”,许多著名品牌是通过广告宣传进入消费者视线的.已知某品牌商品靠广告销售的收入R与广告费A之间满足关系R=a eq \r(A)(a为常数),广告效应为D=a eq \r(A)-A.那么精明的商人为了取得最大广告效应,投入的广告费应为________.(用常数a表示)
eq \f(1,4)a2 [令t= eq \r(A)(t≥0),则A=t2,所以D=at-t2=- eq \b\lc\(\rc\)(\a\vs4\al\c1(t-\f(1,2)a)) eq \s\up8(2)+ eq \f(1,4)a2.所以当t= eq \f(1,2)a,即A= eq \f(1,4)a2时,D取得最大值.]
4.某列火车从A地开往B地,全程277 km.火车出发10 min开出13 km后,以120 km/h的速度匀速行驶.试写出火车行驶的总路程S与匀速行驶的时间t之间的关系,并求火车离开A地2 h内行驶的路程.
[解] 因为火车匀速行驶的时间为(277-13)÷120 = eq \f(11,5) (h),所以0≤t≤ eq \f(11,5).
因为火车匀速行驶t h所行驶的路程为120t,所以火车行驶的总路程S与匀速行驶时间t之间的关系是S=13+120t eq \b\lc\(\rc\)(\a\vs4\al\c1(0≤t≤\f(11,5))).
2 h内火车行驶的路程S=13+120× eq \b\lc\(\rc\)(\a\vs4\al\c1(2-\f(10,60)))=233(km).学 习 目 标
核 心 素 养
1.会用函数图象的变化刻画变化过程.(重点,难点)
2.能够用已知的函数模型刻画实际问题.(难点)
1.在利用函数刻画实际问题的过程中,培养数学抽象素养.
2.在把实际问题转化为数学模型的过程中,提升数学建模素养.
x
4
5
6
7
8
9
10
y
15
17
19
21
23
25
27
数学北师大版 (2019)2.1 实际问题的函数刻画学案设计: 这是一份数学北师大版 (2019)2.1 实际问题的函数刻画学案设计,共8页。
数学2.1 实际问题的函数刻画导学案: 这是一份数学2.1 实际问题的函数刻画导学案,共19页。学案主要包含了教学目标,知识清单,经典例题,课堂达标,能力提升,参考答案等内容,欢迎下载使用。
高中数学北师大版 (2019)必修 第一册2.1 实际问题的函数刻画学案设计: 这是一份高中数学北师大版 (2019)必修 第一册2.1 实际问题的函数刻画学案设计,共3页。学案主要包含了学习目标,学习重难点,学习过程,学习小结,达标检测等内容,欢迎下载使用。













