初中数学人教版八年级上册12.2 三角形全等的判定第3课时导学案

这是一份初中数学人教版八年级上册12.2 三角形全等的判定第3课时导学案，共6页。
01 基础题


知识点1 用“ASA”判定三角形全等


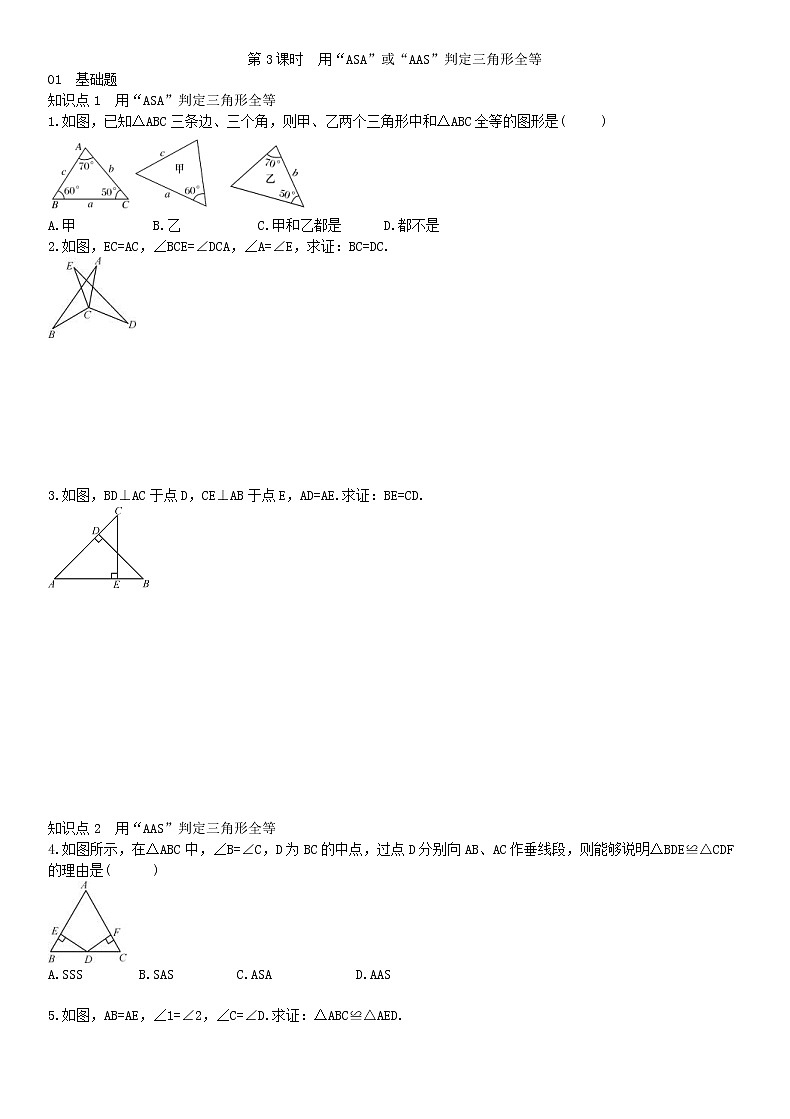
1.如图，已知△ABC三条边、三个角，则甲、乙两个三角形中和△ABC全等的图形是( )





A.甲 B.乙 C.甲和乙都是 D.都不是


2.如图，EC=AC，∠BCE=∠DCA，∠A=∠E，求证：BC=DC.


























3.如图，BD⊥AC于点D，CE⊥AB于点E，AD=AE.求证：BE=CD.






































知识点2 用“AAS”判定三角形全等


4.如图所示，在△ABC中，∠B=∠C，D为BC的中点，过点D分别向AB、AC作垂线段，则能够说明△BDE≌△CDF的理由是( )





A.SSS B.SAS C.ASA D.AAS





5.如图，AB=AE，∠1=∠2，∠C=∠D.求证：△ABC≌△AED.





























6.如图，点E，F在BC上，BE=CF，∠A=∠D，∠B=∠C.求证：AB=DC.















































知识点3 三角形全等判定方法的选用


7.如图，点B，F，C，E在一条直线上，AB∥ED，AC∥FD，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是( )





A.AB=DE B.AC=DF C.∠A=∠D D.BF=EC


8.如图，已知∠ABC=∠BAD，添加下列条件还不能判定△ABC≌△BAD的是( )





A.AC=BD B.∠CAB=∠DBA C.∠C=∠D D.BC=AD





02 中档题


9.如图所示，∠CAB=∠DBA，∠C=∠D，AC、BD相交于点E，下列结论不正确的是( )





A.∠DAE=∠CBE


B.△DEA与△CEB不全等


C.CE=DE


D.EA=EB


10.如图，已知D是△ABC的边AB上一点，DF交AC于点E，DE=EF，FC∥AB，若BD=2，CF=5，则AB长为( )





A.1 B.3 C.5 D.7


11.杨阳同学沿一段笔直的人行道行走，在由A步行到达B处的过程中，通过隔离带的空隙O，刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语，其具体信息如下：


























12.如图，已知点A、F、E、C在同一直线上，AB∥CD，∠ABE=∠CDF，AF=CE.


(1)从图中任找两组全等三角形；


(2)从(1)中任选一组进行证明.
































03 综合题


13.如图1所示，在△ABC中， ∠ACB=90°，AC=BC，过点C在△ABC外作直线MN，AM⊥MN于点M，BN⊥MN于点N.


(1)求证：MN=AM＋BN；


(2)如图2，若过点C作直线MN与线段AB相交，AM⊥MN于点M，BN⊥MN于点N(AM＞BN)，(1)中的结论是否仍然成立？说明理由.

















































































































参考答案


1.(B)


2.证明：∵∠BCE=∠DCA，


∴∠BCE＋∠ACE=∠DCA＋∠ACE，


即∠BCA=∠DCE.


∵AC=EC，∠A=∠E，


∴△BCA≌△DCE(ASA).


∴BC=DC.


3.证明：∵BD⊥AC，CE⊥AB，


∴∠ADB=∠AEC=90°.


在△ABD和△ACE中，


eq \b\lc\{(\a\vs4\al\c1(∠ADB＝∠AEC，,AD＝AE，,∠A＝∠A，))


∴△ABD≌△ACE(ASA).


∴AB=AC.


又∵AD=AE，


∴AB－AE=AC－AD，即BE=CD.


4.(D)


5.证明：∵∠1=∠2，


∴∠1＋∠EAC=∠2＋∠EAC，


即∠BAC=∠EAD.


又∵∠C=∠D，AB=AE，


∴△ABC≌△AED(AAS).


6.证明：∵BE=CF，


∴BF=CE.


在△ABF和△DCE中，


eq \b\lc\{(\a\vs4\al\c1(∠A＝∠D，,∠B＝∠C，,BF＝CE，))


∴△ABF≌△DCE(AAS).


∴AB=DC.


7.(C)


8.(A)


9.(B)


10.(D)


11.解：∵AB∥CD，∴∠ABO=∠CDO.


∵OD⊥CD，∴∠CDO=90°.


∴∠ABO=90°，即OB⊥AB.


∵相邻两平行线间的距离相等，


∴OD=OB.


在△ABO和△CDO中，


eq \b\lc\{(\a\vs4\al\c1(∠ABO＝∠CDO，,OB＝OD，,∠AOB＝∠COD，))


∴△ABO≌△CDO(ASA).


∴CD=AB=20 m.


12.解：(1)△ABE≌△CDF，△AFD≌△CEB(答案不唯一).


(2)选△ABE≌△CDF，


证明：∵AB∥CD，


∴∠BAE=∠DCF.


∵AF=CE，


∴AF＋EF=CE＋EF，即AE=CF.


在△ABE和△CDF中，


eq \b\lc\{(\a\vs4\al\c1(∠BAE＝∠DCF，,∠ABE＝∠CDF，,AE＝CF，))


∴△ABE≌△CDF(AAS).


13.解：(1)证明：∵∠ACB=90°，


∴∠ACM＋∠BCN=90°.


又∵AM⊥MN，BN⊥MN，


∴∠AMC=∠CNB=90°.


∴∠BCN＋∠CBN=90°.


∴∠ACM=∠CBN.


在△ACM和△CBN中，


eq \b\lc\{(\a\vs4\al\c1(∠ACM＝∠CBN，,∠AMC＝∠CNB，,AC＝CB，))


∴△ACM≌△CBN(AAS).


∴MC=NB，MA=NC.


∵MN=MC＋CN，


∴MN=AM＋BN.


(2)(1)中的结论不成立，结论为MN=AM－BN.


理由：同(1)中证明可得△ACM≌△CBN，


∴CM=BN，AM=CN.


∵MN=CN－CM，


∴MN=AM－BN.