数学八年级上册第十二章 全等三角形12.2 三角形全等的判定第2课时学案

这是一份数学八年级上册第十二章 全等三角形12.2 三角形全等的判定第2课时学案，共6页。
01 基础题


知识点1 用“SAS”判定三角形全等


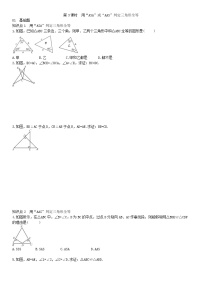
1.下图中全等的三角形有( )





图1 图2 图3 图4


A.图1和图2 B.图2和图3 C.图2和图4 D.图1和图3


2.如图所示，在△ABD和△ACE中，AB=AC，AD=AE，要证△ABD≌△ACE，需补充的条件是( )





A.∠B=∠C B.∠D=∠E C.∠DAE=∠BAC D.∠CAD=∠DAC


3.已知：如图，OA=OB，OC平分∠AOB，求证：△AOC≌△BOC.




















4.如图，已知B，E，F，C四个点在同一条直线上，AB=CD，BE=CF，∠B=∠C，求证：△ABF≌△DCE.









































知识点2 全等三角形的判定与性质的综合


5.如图，C是线段AB的中点，CD=BE，CD∥BE.求证：∠D=∠E.



































6.如图，已知△ABC和△DAE，D是AC上一点，AD=AB，DE∥AB，DE=AC.求证：AE=BC.





























知识点3 利用“SAS”判定三角形全等解决实际问题


7.如图，将两根钢条AA′，BB′的中点O连在一起，使AA′，BB′可以绕着点O自由转动，就做成了一个测量工件，则AB的长等于内槽宽A′B′，那么判定△AOB≌△A′OB′的理由是( )





A.边角边 B.角边角 C.边边边 D.角角边





8.如图所示，有一块三角形镜子，小明不小心将它打破成1、2两块，现需配成同样大小的一面镜子.为了方便起见，需带上1块，其理由是 .





02 中档题


9.如图，已知AB=AC，AD=AE，若要得到“△ABD≌△ACE”，必须添加一个条件，则下列所添条件不成立的是( )





A.BD=CE B.∠ABD=∠ACE C.∠BAD=∠CAE D.∠BAC=∠DAE


10.如图，在四边形ABCD中，AB=AD，CB=CD，若连接AC、BD相交于点O，则图中全等三角形共有( )





A.1对 B.2对 C.3对 D.4对


11.如图，点A在BE上，AD=AE，AB=AC，∠1=∠2=30°，则∠3的度数为 .





12.如图所示，A，B，C，D是四个村庄，B，D，C在一条东西走向公路的沿线上，BD=1 km，DC=1 km，村庄AC，AD间也有公路相连，且公路AD是南北走向，AC=3 km，只有AB之间由于间隔了一个小湖，所以无直接相连的公路.现决定在湖面上造一座斜拉桥，测得AE=1.2 km，BF=0.7 km，则建造的斜拉桥长至少有 km.








13.如图，已知点B，E，C，F在一条直线上，AB=DF，AC=DE，∠A=∠D.


(1)求证：AC∥DE；


(2)若BF=13，EC=5，求BC的长.






































14.如图所示，A，F，C，D四点同在一直线上，AF=CD，AB∥DE，且AB=DE.求证：





(1)△ABC≌△DEF；


(2)∠CBF=∠FEC.
































03 综合题


15.如图，在四边形ABCD中，∠A=∠BCD=90°，BC=DC.延长AD到E点，使DE=AB.求证：


(1)∠ABC=∠EDC；


(2)△ABC≌△EDC.






























































参考答案


1.(D)


2.(C)


3.证明：∵OC平分∠AOB，


∴∠AOC=∠BOC.


在△AOC和△BOC中，


eq \b\lc\{(\a\vs4\al\c1(OA＝OB，,∠AOC＝∠BOC，,OC＝OC，))


∴△AOC≌△BOC(SAS).


4.证明：∵BE=CF，


∴BE＋EF=CF＋EF，即BF=CE.


在△ABF和△DCE中，


eq \b\lc\{(\a\vs4\al\c1(AB＝DC，,∠B＝∠C，,BF＝CE，))


∴△ABF≌△DCE(SAS).


5.证明：∵C是线段AB的中点，


∴AC=CB.


∵CD∥BE，∴∠ACD=∠CBE.


在△ACD和△CBE中，


eq \b\lc\{(\a\vs4\al\c1(AC＝CB，,∠ACD＝∠CBE，,CD＝BE，))


∴△ACD≌△CBE.


∴∠D=∠E.


6.证明：∵DE∥AB，


∴∠ADE=∠BAC.


在△ADE和△BAC中，eq \b\lc\{(\a\vs4\al\c1(AD＝BA，,∠ADE＝∠BAC，,DE＝AC，))


∴△ADE≌△BAC(SAS).


∴AE=BC.


7.(A)


8.两边及其夹角分别相等的两个三角形全等.


9.(B)


10.(C)


11.30°.





13.解：(1)证明：在△ABC和△DFE中，


eq \b\lc\{(\a\vs4\al\c1(AB＝DF，,∠A＝∠D，,AC＝DE，))


∴△ABC≌△DFE(SAS).


∴∠ACE=∠DEF.


∴AC∥DE.


(2)∵△ABC≌△DFE，


∴BC=EF.


∴CB－EC=EF－EC，即EB=CF.


∵BF=13，EC=5，∴EB=eq \f(13－5,2)=4.


∴CB=4＋5=9.


14.证明：(1)∵AB∥DE，


∴∠A=∠D.


又∵AF=CD，


∴AF＋FC=CD＋FC.


∴AC=DF.


∵AB=DE，


∴△ABC≌△DEF(SAS).


(2)∵△ABC≌△DEF，


∴BC=EF，∠ACB=∠DFE.


∵FC=CF，


∴△FBC≌△CEF(SAS).


∴∠CBF=∠FEC.


15.证明：(1)在四边形ABCD中，


∵∠BAD=∠BCD=90°，


∴∠B＋∠ADC=180°.


又∵∠CDE＋∠ADC=180°.


∴∠ABC=∠EDC.


(2)连接AC.


在△ABC和△EDC中，


eq \b\lc\{(\a\vs4\al\c1(AB＝ED，,∠ABC＝∠EDC，,CB＝CD，))


∴△ABC≌△EDC(SAS).