

还剩14页未读,
继续阅读
2019-2020学年广东省广州市越秀区七年级(下)期末数学试卷
展开
2019-2020学年广东省广州市越秀区七年级(下)期末数学试卷
一、选择题:本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(3分)在平面直角坐标系中,点P(1,﹣2)位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(3分)下列调查中,适宜采用全面调查的是( )
A.调查某池塘中现有鱼的数量
B.调查某批次汽车的抗撞击能力
C.选出某班短跑最快的学生参加全校短跑比赛
D.调查市场上某种食品的色素含量是否符合国家标准
3.(3分)下列判断正确的是( )
A.<2 B.<2 C.π=3.14 D.
4.(3分)如图,ABCD是四边形,下列条件中可以判定AD∥BC的是( )
A.∠ABD=∠BDC B.∠ABC+∠BCD=180°
C.∠BAD=∠BCD D.∠ADC+∠BCD=180°
5.(3分)由2x﹣3y=1可以得到用x表示y的式子为( )
A.y=x﹣1 B.y= C.y=1﹣x D.y=
6.(3分)下列命题中是假命题的是( )
A.若x2=2,则x=±
B.若x2=3,则x是一个无理数
C.若a>b,则a+c>b+c
D.若ac>bc,则a>b
7.(3分)如果点P(1+m,2﹣m)在第二象限,那么m的取值范围是( )
A.m<﹣1 B.m<2 C.﹣1<m<2 D.m>2
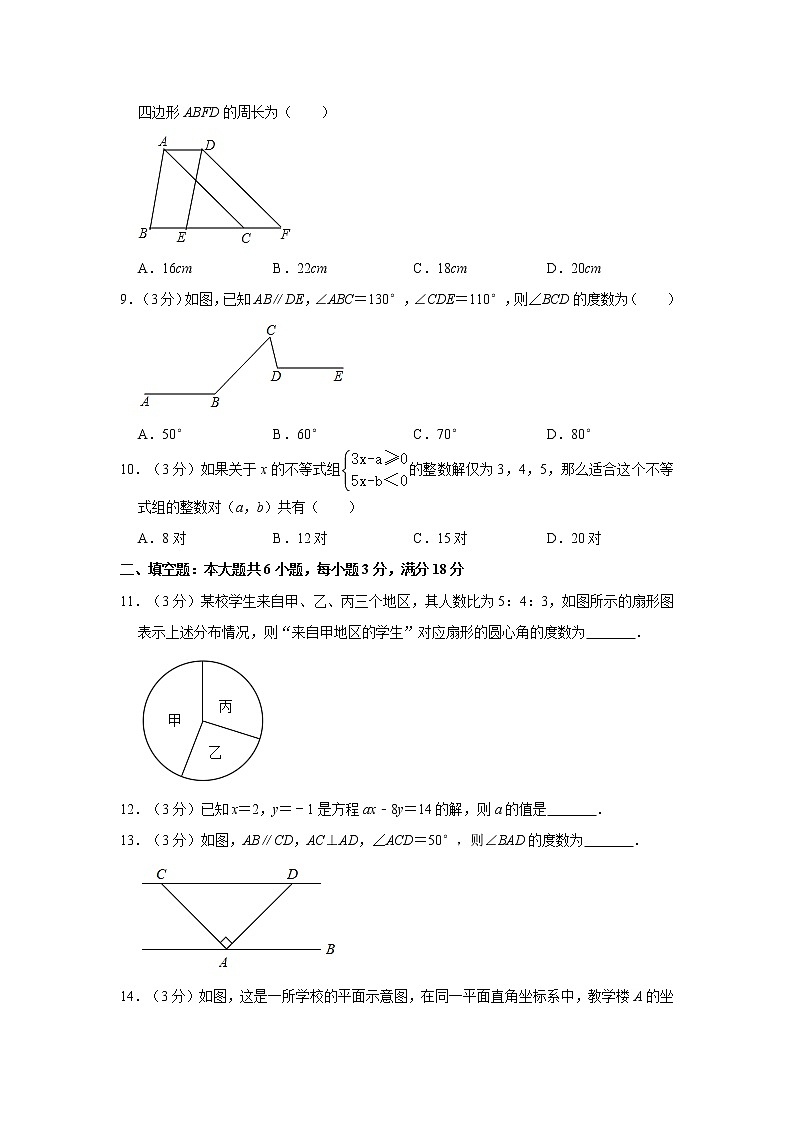
8.(3分)如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为18cm,则四边形ABFD的周长为( )
A.16cm B.22cm C.18cm D.20cm
9.(3分)如图,已知AB∥DE,∠ABC=130°,∠CDE=110°,则∠BCD的度数为( )
A.50° B.60° C.70° D.80°
10.(3分)如果关于x的不等式组的整数解仅为3,4,5,那么适合这个不等式组的整数对(a,b)共有( )
A.8对 B.12对 C.15对 D.20对
二、填空题:本大题共6小题,每小题3分,满分18分
11.(3分)某校学生来自甲、乙、丙三个地区,其人数比为5:4:3,如图所示的扇形图表示上述分布情况,则“来自甲地区的学生”对应扇形的圆心角的度数为 .
12.(3分)已知x=2,y=﹣1是方程ax﹣8y=14的解,则a的值是 .
13.(3分)如图,AB∥CD,AC⊥AD,∠ACD=50°,则∠BAD的度数为 .
14.(3分)如图,这是一所学校的平面示意图,在同一平面直角坐标系中,教学楼A的坐标为(﹣3,0),实验楼B的坐标为(2,0),则图书馆C的坐标为 .
15.(3分)若(a﹣3)2+=0,则a+b的立方根是 .
16.(3分)甲和乙同时从A地出发,匀速行走到B地.甲走完一半路程时,乙才走了4千米,乙走完一半路程时,甲已走了9千米.当甲走完全程时,乙未走完的路程还有 千米.
三、解答题:本大题共7小题,满分72分.解答须写出文字说明、推理过程和演算步骤
17.(10分)如图,已知∠AOB=60°,点P在∠AOB的内部,用三角板与量角器作图,并回答问题:
(1)过点P作PC∥OB,交OA于C,并求∠OCP的度数;
(2)过点P作PD⊥OB,垂足为D,连接OP,并比较线段OP与PD的大小.
18.(10分)求下列各式中x的值
(1)25x2=4;
(2)(x+1)3=﹣27.
19.(10分)解不等式组并把解集在数轴上表示出来.
20.(10分)某家庭记录了使用节水龙头的日用水量样本数据(单位:m3),得到频数分布表如下:
日用水量x
频数
百分比
0≤x<0.1
1
4%
0.1≤x<0.2
2
8%
0.2≤x<0.3
a
20%
0.3≤x<0.4
b
32%
0.4≤x<0.5
6
c
0.5≤x<0.6
3
12%
(1)求a,b,c的值;
(2)在图上补全频数分布直方图;
(3)估计该家庭使用节水龙头100天后,其中日用水量小于0.4m3的天数是多少天?
21.(10分)如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别是A(﹣5,3),B(﹣3,1),C(﹣2,2).将△ABC先向下平移5个单位长度,然后向右平移6个单位长度,再作关于x轴对称的图形,得到△A1B1C1.
(1)写出点A1,B1,C1的坐标;
(2)在平面直角坐标系xOy中画出△A1B1C1;
(3)求△A1B1C1的面积.
22.(10分)有大小两种货车,3辆大货车与2辆小货车一次可以运货17吨,5辆大货车与6辆小货车一次可以运货35吨,那么3辆大货车与6辆小货车一次可以运货多少吨?
23.(12分)如图1,已知∠ACB=80°,点A在直线EF上,点B在直线GH上,且∠CAE+∠CBG=80°.
(1)试判断直线EF与GH的位置关系,并说明理由;
(2)如图2,若点B在直线GH上运动,作∠CAP=2∠CAE,作∠CBP=2∠CBG,试判断∠APB的大小是否会随着点B的运动而发生变化?若不变,求出∠APB的大小;若变化,请说明理由.
2019-2020学年广东省广州市越秀区七年级(下)期末数学试卷
参考答案与试题解析
一、选择题:本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(3分)在平面直角坐标系中,点P(1,﹣2)位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】根据第四象限内的点的横坐标大于零,纵坐标小于零,可得答案.
【解答】解:在平面直角坐标系中,点P(1,﹣2)位于第四象限,
故选:D.
2.(3分)下列调查中,适宜采用全面调查的是( )
A.调查某池塘中现有鱼的数量
B.调查某批次汽车的抗撞击能力
C.选出某班短跑最快的学生参加全校短跑比赛
D.调查市场上某种食品的色素含量是否符合国家标准
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【解答】解:A.调查某池塘中现有鱼的数量,应采用抽样调查,故此选项不合题意;
B.调查某批次汽车的抗撞击能力,应采用抽样调查,故此选项不合题意;
C.选出某班短跑最快的学生参加全校短跑比赛,适宜采用全面调查,故此选项符合题意;
D.调查市场上某种食品的色素含量是否符合国家标准,应采用抽样调查,故此选项不合题意.
故选:C.
3.(3分)下列判断正确的是( )
A.<2 B.<2 C.π=3.14 D.
【分析】估算无理数,进行比较即可得出答案.
【解答】解:∵<<,∴1<<2,因此选项A符合题意,
∵23=8<9,∴>2,因此选项B不符合题意;
∵π是一个无限不循环小数,即π=3.1415926……,因此选项C不符合题意;
=0.3333……,=0.333……,因此选项D不符合题意;
故选:A.
4.(3分)如图,ABCD是四边形,下列条件中可以判定AD∥BC的是( )
A.∠ABD=∠BDC B.∠ABC+∠BCD=180°
C.∠BAD=∠BCD D.∠ADC+∠BCD=180°
【分析】根据平行线的判定定理逐个判断即可.
【解答】解:A、根据∠ABD=∠BDC能推出AB∥CD,不能推出AD∥BC,故本选项不符合题意;
B、根据∠ABC+∠BCD=180°能推出AB∥CD,不能推出AD∥BC,故本选项不符合题意;
C、根据∠BAD=∠BCD不能推出AD∥BC,故本选项不符合题意;
D、根据∠ADC+∠BCD=180°能推出AD∥BC(同旁内角互补,两直线平行),故本选项符合题意;
故选:D.
5.(3分)由2x﹣3y=1可以得到用x表示y的式子为( )
A.y=x﹣1 B.y= C.y=1﹣x D.y=
【分析】把x看做已知数求出y即可.
【解答】解:方程2x﹣3y=1,
移项得:﹣3y=1﹣2x,
解得:y==.
故选:B.
6.(3分)下列命题中是假命题的是( )
A.若x2=2,则x=±
B.若x2=3,则x是一个无理数
C.若a>b,则a+c>b+c
D.若ac>bc,则a>b
【分析】根据平方根的定义对A进行判断;根据平方根的定义和无理数的定义对B进行判断;根据不等式的性质对C、D进行判断.
【解答】解:A、若x2=2,则x=±,所以A选项为真命题;
B、若x2=3,则x=±,所以x为无理数,所以B选项为真命题;
C、若a>b,则a+c>b+c,所以C选项为真命题;
D、若ac>bc,当c>0时,a>b,所以D选项为假命题.
故选:D.
7.(3分)如果点P(1+m,2﹣m)在第二象限,那么m的取值范围是( )
A.m<﹣1 B.m<2 C.﹣1<m<2 D.m>2
【分析】根据第二象限点的坐标特征列出关于m的不等式组,求出不等式组的解集即可求出m的范围.
【解答】解:∵点P(1+m,2﹣m)在第二象限,
∴,
解得:m<﹣1,
则m的取值范围是m<﹣1.
故选:A.
8.(3分)如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为18cm,则四边形ABFD的周长为( )
A.16cm B.22cm C.18cm D.20cm
【分析】根据平移的性质可得DF=AC,再求出四边形ABFD的周长等于△ABC的周长加上AD与CF,然后计算即可得解.
【解答】解:∵△ABC沿BC方向平移2cm得到△DEF,
∴DF=AC,AD=CF=2cm,
∴四边形ABFD的周长=AB+BF+DF+AD
=AB+BC+CF+AC+AD
=△ABC的周长+AD+CF
=18+2+2
=22cm.
故选:B.
9.(3分)如图,已知AB∥DE,∠ABC=130°,∠CDE=110°,则∠BCD的度数为( )
A.50° B.60° C.70° D.80°
【分析】作DE的反向延长线交BC于M,根据平行线的性质得出∠BMD=∠ABC=130°,求出∠CMD的度数,根据三角形的外角性质得出∠BCD=∠CDE﹣∠CMD,代入求出即可.
【解答】解:
作DE的反向延长线交BC于M,
∵AB∥DE,∠ABC=130°,
∴∠BMD=∠ABC=130°,
∴∠CMD=180°﹣∠BMD=50°,
∵∠CDE=110°,
∴∠BCD=∠CDE﹣∠CMD=110°﹣50°=60°,
故选:B.
10.(3分)如果关于x的不等式组的整数解仅为3,4,5,那么适合这个不等式组的整数对(a,b)共有( )
A.8对 B.12对 C.15对 D.20对
【分析】首先解不等式组,用a,b表示出不等式组的解集,根据不等式的整数解仅有3,4,5,即可确定a,b的值,从而求解.
【解答】解:解不等式组,得:≤x<,
∵整数解仅有3,4,5,
∴2<≤3,5<≤6,
解得:6<a≤9,25<b≤30,
∴a=7,8,9,b=26,27,28,29,30.
则整数a,b组成的有序数对(a,b)共有15对.
故选:C.
二、填空题:本大题共6小题,每小题3分,满分18分
11.(3分)某校学生来自甲、乙、丙三个地区,其人数比为5:4:3,如图所示的扇形图表示上述分布情况,则“来自甲地区的学生”对应扇形的圆心角的度数为 150° .
【分析】用甲地区所占百分比乘以360°即可求得答案.
【解答】解:“来自甲地区的学生”对应扇形的圆心角的度数为360°×=150°,
故答案为:150°.
12.(3分)已知x=2,y=﹣1是方程ax﹣8y=14的解,则a的值是 3 .
【分析】把x=2,y=﹣1代入方程得出2a+8=14,求出方程的解即可.
【解答】解:∵x=2,y=﹣1是方程ax﹣8y=14的解,
∴代入得:2a+8=14,
解得:a=3,
故答案为:3.
13.(3分)如图,AB∥CD,AC⊥AD,∠ACD=50°,则∠BAD的度数为 40° .
【分析】求出∠CAD=90°,根据三角形你的内角和定理求出∠ADC=40°,根据平行线的性质得出∠BAD=∠ADC,代入求出即可.
【解答】解:∵AC⊥AD,
∴∠CAD=90°,
∵∠ACD=50°,
∴∠ADC=180°﹣∠CAD﹣∠ACD=40°,
∵AB∥CD,
∴∠BAD=∠ADC=40°,
故答案为:40°.
14.(3分)如图,这是一所学校的平面示意图,在同一平面直角坐标系中,教学楼A的坐标为(﹣3,0),实验楼B的坐标为(2,0),则图书馆C的坐标为 (﹣1,﹣3) .
【分析】直接利用已知点坐标进而建立平面直角坐标系,即可得出C点坐标.
【解答】解:如图所示:图书馆C的坐标为(﹣1,﹣3).
故答案为:(﹣1,﹣3).
15.(3分)若(a﹣3)2+=0,则a+b的立方根是 2 .
【分析】根据非负数的性质列式求出a、b的值,然后代入代数式进行计算,再根据立方根的定义解答.
【解答】解:由题意得,a﹣3=0,b﹣5=0,
解得a=3,b=5,
所以,a+b=3+5=8,
所以,a+b的立方根是2.
故答案为:2.
16.(3分)甲和乙同时从A地出发,匀速行走到B地.甲走完一半路程时,乙才走了4千米,乙走完一半路程时,甲已走了9千米.当甲走完全程时,乙未走完的路程还有 4 千米.
【分析】设A,B两地之间的路程为x千米,根据两人的速度之比为定值,即可得出关于x的分式方程,解之经检验后即可得出结论,再结合“甲走完一半路程时,乙才走了4千米”,即可求出结论.
【解答】解:设A,B两地之间的路程为x千米,
依题意,得:=,
化简,得:x2=144,
解得:x1=12,x2=﹣12,
经检验,x1=12,x2=﹣12均为原方程的解,x1=12符合题意,x2=﹣12不符合题意,舍去,
∴x﹣4×2=4.
故答案为:4.
三、解答题:本大题共7小题,满分72分.解答须写出文字说明、推理过程和演算步骤
17.(10分)如图,已知∠AOB=60°,点P在∠AOB的内部,用三角板与量角器作图,并回答问题:
(1)过点P作PC∥OB,交OA于C,并求∠OCP的度数;
(2)过点P作PD⊥OB,垂足为D,连接OP,并比较线段OP与PD的大小.
【分析】(1)连接OP,作∠CPO=∠POD即可,再利用平行线的性质求解即可.
(2)根据垂线段最短即可判断.
【解答】解:(1)如图,直线PC即为所求.
∵PC∥OD,
∴∠OCP+∠AOB=180°,
∵∠AOB=60°,
∴∠OCP=120°.
(2)∵PD⊥OB,
∴PD<OP.
18.(10分)求下列各式中x的值
(1)25x2=4;
(2)(x+1)3=﹣27.
【分析】(1)根据等式的性质,可得平方的形式,根据开方运算,可得答案;
(2)根据开立方运算,可得一元一次方程,根据解方程,可得答案.
【解答】解:(1)方程两边都除以25,得
x2=,
开方得,
x=;
(2)开立方得,
x+1=﹣3,
移项得,
x=﹣4.
19.(10分)解不等式组并把解集在数轴上表示出来.
【分析】分别求出不等式组中两不等式的解集,找出两解集的公共部分确定出不等式组的解集,表示在数轴上即可.
【解答】解:由①得:x>﹣2,
由②得:x≤3,
∴不等式组的解集为﹣2<x≤3,
20.(10分)某家庭记录了使用节水龙头的日用水量样本数据(单位:m3),得到频数分布表如下:
日用水量x
频数
百分比
0≤x<0.1
1
4%
0.1≤x<0.2
2
8%
0.2≤x<0.3
a
20%
0.3≤x<0.4
b
32%
0.4≤x<0.5
6
c
0.5≤x<0.6
3
12%
(1)求a,b,c的值;
(2)在图上补全频数分布直方图;
(3)估计该家庭使用节水龙头100天后,其中日用水量小于0.4m3的天数是多少天?
【分析】(1)根据频数、总数、频率之间的关系进行计算即可;
(2)根据频数分布表,和a、b的值,即可补全频数分布直方图;
(3)样本中日用水量小于0.4m3的天数占调查天数的4%+8%+20%+32%=64%,因此估计100天的64%是4日用水量小于0.4m3的天数占调查天数.
【解答】解:(1)1÷4%=25,a=25×20%=5,b=25×32%=8,c=6÷25=24%,
答:a、b、c的值分别为5,8,24%;
(2)补全频数分布直方图如图所示:
(3)100×(4%+8%+20%+32%)=64(天),
答:该家庭使用节水龙头100天后,其中日用水量小于0.4m3的天数是64天.
21.(10分)如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别是A(﹣5,3),B(﹣3,1),C(﹣2,2).将△ABC先向下平移5个单位长度,然后向右平移6个单位长度,再作关于x轴对称的图形,得到△A1B1C1.
(1)写出点A1,B1,C1的坐标;
(2)在平面直角坐标系xOy中画出△A1B1C1;
(3)求△A1B1C1的面积.
【分析】(1)根据平移规律写出坐标即可.
(2)根据坐标画出图形即可.
(3)利用分割法求出三角形的面积即可.
【解答】解:(1)A1(1,2),B2(3,4),C1(4,3).
(2)如图△A1B1C1即为所求.
(3)=2×3﹣×2×2﹣×1×1﹣×1×3=2.
22.(10分)有大小两种货车,3辆大货车与2辆小货车一次可以运货17吨,5辆大货车与6辆小货车一次可以运货35吨,那么3辆大货车与6辆小货车一次可以运货多少吨?
【分析】设每辆大货车一次可以运货x吨,每辆小货车一次可以运货y吨,根据“3辆大货车与2辆小货车一次可以运货17吨,5辆大货车与6辆小货车一次可以运货35吨”,即可得出关于x,y的二元一次方程组,解之即可得出x,y的值,再将其代入(3x+6y)中即可求出结论.
【解答】解:设每辆大货车一次可以运货x吨,每辆小货车一次可以运货y吨,
依题意,得:,
解得:,
∴3x+6y=3×4+6×=27.
答:3辆大货车与6辆小货车一次可以运货27吨.
23.(12分)如图1,已知∠ACB=80°,点A在直线EF上,点B在直线GH上,且∠CAE+∠CBG=80°.
(1)试判断直线EF与GH的位置关系,并说明理由;
(2)如图2,若点B在直线GH上运动,作∠CAP=2∠CAE,作∠CBP=2∠CBG,试判断∠APB的大小是否会随着点B的运动而发生变化?若不变,求出∠APB的大小;若变化,请说明理由.
【分析】(1)如图1,过点C作CD∥EF,可得∠CAE=∠ACD,由∠ACB=∠ACD+∠BCD=80°,∠CAE+∠CBG=80°.可得∠BCD=∠CBG,得CD∥GH,进而可得直线EF与GH的位置关系;
(2)根据已知条件可得∠CAP+∠CBP=2(∠CAE+∠CBG)=160°,再根据四边形内角和等于360度即可求出∠APB的大小.
【解答】解;(1)直线EF与GH的位置关系是平行,理由如下:
如图1,过点C作CD∥EF,
∴∠CAE=∠ACD,
∵∠ACB=∠ACD+∠BCD=80°,∠CAE+∠CBG=80°.
∴∠BCD=∠CBG,
∴CD∥GH,
∴EF∥GH;
(2)∠APB的大小不会随着点B的运动而发生变化,理由如下:
如图2,∵∠CAP=2∠CAE,∠CBP=2∠CBG,
∴∠CAP+∠CBP=2∠CAE+2∠CBG=2(∠CAE+∠CBG)=2×80°=160°,
∴∠APB=360°﹣∠ACB﹣(∠CAP+∠CBP)=360°﹣80°﹣160°=120°.
所以∠APB的大小为120°.
一、选择题:本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(3分)在平面直角坐标系中,点P(1,﹣2)位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(3分)下列调查中,适宜采用全面调查的是( )
A.调查某池塘中现有鱼的数量
B.调查某批次汽车的抗撞击能力
C.选出某班短跑最快的学生参加全校短跑比赛
D.调查市场上某种食品的色素含量是否符合国家标准
3.(3分)下列判断正确的是( )
A.<2 B.<2 C.π=3.14 D.
4.(3分)如图,ABCD是四边形,下列条件中可以判定AD∥BC的是( )
A.∠ABD=∠BDC B.∠ABC+∠BCD=180°
C.∠BAD=∠BCD D.∠ADC+∠BCD=180°
5.(3分)由2x﹣3y=1可以得到用x表示y的式子为( )
A.y=x﹣1 B.y= C.y=1﹣x D.y=
6.(3分)下列命题中是假命题的是( )
A.若x2=2,则x=±
B.若x2=3,则x是一个无理数
C.若a>b,则a+c>b+c
D.若ac>bc,则a>b
7.(3分)如果点P(1+m,2﹣m)在第二象限,那么m的取值范围是( )
A.m<﹣1 B.m<2 C.﹣1<m<2 D.m>2
8.(3分)如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为18cm,则四边形ABFD的周长为( )
A.16cm B.22cm C.18cm D.20cm
9.(3分)如图,已知AB∥DE,∠ABC=130°,∠CDE=110°,则∠BCD的度数为( )
A.50° B.60° C.70° D.80°
10.(3分)如果关于x的不等式组的整数解仅为3,4,5,那么适合这个不等式组的整数对(a,b)共有( )
A.8对 B.12对 C.15对 D.20对
二、填空题:本大题共6小题,每小题3分,满分18分
11.(3分)某校学生来自甲、乙、丙三个地区,其人数比为5:4:3,如图所示的扇形图表示上述分布情况,则“来自甲地区的学生”对应扇形的圆心角的度数为 .
12.(3分)已知x=2,y=﹣1是方程ax﹣8y=14的解,则a的值是 .
13.(3分)如图,AB∥CD,AC⊥AD,∠ACD=50°,则∠BAD的度数为 .
14.(3分)如图,这是一所学校的平面示意图,在同一平面直角坐标系中,教学楼A的坐标为(﹣3,0),实验楼B的坐标为(2,0),则图书馆C的坐标为 .
15.(3分)若(a﹣3)2+=0,则a+b的立方根是 .
16.(3分)甲和乙同时从A地出发,匀速行走到B地.甲走完一半路程时,乙才走了4千米,乙走完一半路程时,甲已走了9千米.当甲走完全程时,乙未走完的路程还有 千米.
三、解答题:本大题共7小题,满分72分.解答须写出文字说明、推理过程和演算步骤
17.(10分)如图,已知∠AOB=60°,点P在∠AOB的内部,用三角板与量角器作图,并回答问题:
(1)过点P作PC∥OB,交OA于C,并求∠OCP的度数;
(2)过点P作PD⊥OB,垂足为D,连接OP,并比较线段OP与PD的大小.
18.(10分)求下列各式中x的值
(1)25x2=4;
(2)(x+1)3=﹣27.
19.(10分)解不等式组并把解集在数轴上表示出来.
20.(10分)某家庭记录了使用节水龙头的日用水量样本数据(单位:m3),得到频数分布表如下:
日用水量x
频数
百分比
0≤x<0.1
1
4%
0.1≤x<0.2
2
8%
0.2≤x<0.3
a
20%
0.3≤x<0.4
b
32%
0.4≤x<0.5
6
c
0.5≤x<0.6
3
12%
(1)求a,b,c的值;
(2)在图上补全频数分布直方图;
(3)估计该家庭使用节水龙头100天后,其中日用水量小于0.4m3的天数是多少天?
21.(10分)如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别是A(﹣5,3),B(﹣3,1),C(﹣2,2).将△ABC先向下平移5个单位长度,然后向右平移6个单位长度,再作关于x轴对称的图形,得到△A1B1C1.
(1)写出点A1,B1,C1的坐标;
(2)在平面直角坐标系xOy中画出△A1B1C1;
(3)求△A1B1C1的面积.
22.(10分)有大小两种货车,3辆大货车与2辆小货车一次可以运货17吨,5辆大货车与6辆小货车一次可以运货35吨,那么3辆大货车与6辆小货车一次可以运货多少吨?
23.(12分)如图1,已知∠ACB=80°,点A在直线EF上,点B在直线GH上,且∠CAE+∠CBG=80°.
(1)试判断直线EF与GH的位置关系,并说明理由;
(2)如图2,若点B在直线GH上运动,作∠CAP=2∠CAE,作∠CBP=2∠CBG,试判断∠APB的大小是否会随着点B的运动而发生变化?若不变,求出∠APB的大小;若变化,请说明理由.
2019-2020学年广东省广州市越秀区七年级(下)期末数学试卷
参考答案与试题解析
一、选择题:本大题共10小题,每小题3分,满分30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(3分)在平面直角坐标系中,点P(1,﹣2)位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】根据第四象限内的点的横坐标大于零,纵坐标小于零,可得答案.
【解答】解:在平面直角坐标系中,点P(1,﹣2)位于第四象限,
故选:D.
2.(3分)下列调查中,适宜采用全面调查的是( )
A.调查某池塘中现有鱼的数量
B.调查某批次汽车的抗撞击能力
C.选出某班短跑最快的学生参加全校短跑比赛
D.调查市场上某种食品的色素含量是否符合国家标准
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
【解答】解:A.调查某池塘中现有鱼的数量,应采用抽样调查,故此选项不合题意;
B.调查某批次汽车的抗撞击能力,应采用抽样调查,故此选项不合题意;
C.选出某班短跑最快的学生参加全校短跑比赛,适宜采用全面调查,故此选项符合题意;
D.调查市场上某种食品的色素含量是否符合国家标准,应采用抽样调查,故此选项不合题意.
故选:C.
3.(3分)下列判断正确的是( )
A.<2 B.<2 C.π=3.14 D.
【分析】估算无理数,进行比较即可得出答案.
【解答】解:∵<<,∴1<<2,因此选项A符合题意,
∵23=8<9,∴>2,因此选项B不符合题意;
∵π是一个无限不循环小数,即π=3.1415926……,因此选项C不符合题意;
=0.3333……,=0.333……,因此选项D不符合题意;
故选:A.
4.(3分)如图,ABCD是四边形,下列条件中可以判定AD∥BC的是( )
A.∠ABD=∠BDC B.∠ABC+∠BCD=180°
C.∠BAD=∠BCD D.∠ADC+∠BCD=180°
【分析】根据平行线的判定定理逐个判断即可.
【解答】解:A、根据∠ABD=∠BDC能推出AB∥CD,不能推出AD∥BC,故本选项不符合题意;
B、根据∠ABC+∠BCD=180°能推出AB∥CD,不能推出AD∥BC,故本选项不符合题意;
C、根据∠BAD=∠BCD不能推出AD∥BC,故本选项不符合题意;
D、根据∠ADC+∠BCD=180°能推出AD∥BC(同旁内角互补,两直线平行),故本选项符合题意;
故选:D.
5.(3分)由2x﹣3y=1可以得到用x表示y的式子为( )
A.y=x﹣1 B.y= C.y=1﹣x D.y=
【分析】把x看做已知数求出y即可.
【解答】解:方程2x﹣3y=1,
移项得:﹣3y=1﹣2x,
解得:y==.
故选:B.
6.(3分)下列命题中是假命题的是( )
A.若x2=2,则x=±
B.若x2=3,则x是一个无理数
C.若a>b,则a+c>b+c
D.若ac>bc,则a>b
【分析】根据平方根的定义对A进行判断;根据平方根的定义和无理数的定义对B进行判断;根据不等式的性质对C、D进行判断.
【解答】解:A、若x2=2,则x=±,所以A选项为真命题;
B、若x2=3,则x=±,所以x为无理数,所以B选项为真命题;
C、若a>b,则a+c>b+c,所以C选项为真命题;
D、若ac>bc,当c>0时,a>b,所以D选项为假命题.
故选:D.
7.(3分)如果点P(1+m,2﹣m)在第二象限,那么m的取值范围是( )
A.m<﹣1 B.m<2 C.﹣1<m<2 D.m>2
【分析】根据第二象限点的坐标特征列出关于m的不等式组,求出不等式组的解集即可求出m的范围.
【解答】解:∵点P(1+m,2﹣m)在第二象限,
∴,
解得:m<﹣1,
则m的取值范围是m<﹣1.
故选:A.
8.(3分)如图,将△ABC沿BC方向平移2cm得到△DEF,若△ABC的周长为18cm,则四边形ABFD的周长为( )
A.16cm B.22cm C.18cm D.20cm
【分析】根据平移的性质可得DF=AC,再求出四边形ABFD的周长等于△ABC的周长加上AD与CF,然后计算即可得解.
【解答】解:∵△ABC沿BC方向平移2cm得到△DEF,
∴DF=AC,AD=CF=2cm,
∴四边形ABFD的周长=AB+BF+DF+AD
=AB+BC+CF+AC+AD
=△ABC的周长+AD+CF
=18+2+2
=22cm.
故选:B.
9.(3分)如图,已知AB∥DE,∠ABC=130°,∠CDE=110°,则∠BCD的度数为( )
A.50° B.60° C.70° D.80°
【分析】作DE的反向延长线交BC于M,根据平行线的性质得出∠BMD=∠ABC=130°,求出∠CMD的度数,根据三角形的外角性质得出∠BCD=∠CDE﹣∠CMD,代入求出即可.
【解答】解:
作DE的反向延长线交BC于M,
∵AB∥DE,∠ABC=130°,
∴∠BMD=∠ABC=130°,
∴∠CMD=180°﹣∠BMD=50°,
∵∠CDE=110°,
∴∠BCD=∠CDE﹣∠CMD=110°﹣50°=60°,
故选:B.
10.(3分)如果关于x的不等式组的整数解仅为3,4,5,那么适合这个不等式组的整数对(a,b)共有( )
A.8对 B.12对 C.15对 D.20对
【分析】首先解不等式组,用a,b表示出不等式组的解集,根据不等式的整数解仅有3,4,5,即可确定a,b的值,从而求解.
【解答】解:解不等式组,得:≤x<,
∵整数解仅有3,4,5,
∴2<≤3,5<≤6,
解得:6<a≤9,25<b≤30,
∴a=7,8,9,b=26,27,28,29,30.
则整数a,b组成的有序数对(a,b)共有15对.
故选:C.
二、填空题:本大题共6小题,每小题3分,满分18分
11.(3分)某校学生来自甲、乙、丙三个地区,其人数比为5:4:3,如图所示的扇形图表示上述分布情况,则“来自甲地区的学生”对应扇形的圆心角的度数为 150° .
【分析】用甲地区所占百分比乘以360°即可求得答案.
【解答】解:“来自甲地区的学生”对应扇形的圆心角的度数为360°×=150°,
故答案为:150°.
12.(3分)已知x=2,y=﹣1是方程ax﹣8y=14的解,则a的值是 3 .
【分析】把x=2,y=﹣1代入方程得出2a+8=14,求出方程的解即可.
【解答】解:∵x=2,y=﹣1是方程ax﹣8y=14的解,
∴代入得:2a+8=14,
解得:a=3,
故答案为:3.
13.(3分)如图,AB∥CD,AC⊥AD,∠ACD=50°,则∠BAD的度数为 40° .
【分析】求出∠CAD=90°,根据三角形你的内角和定理求出∠ADC=40°,根据平行线的性质得出∠BAD=∠ADC,代入求出即可.
【解答】解:∵AC⊥AD,
∴∠CAD=90°,
∵∠ACD=50°,
∴∠ADC=180°﹣∠CAD﹣∠ACD=40°,
∵AB∥CD,
∴∠BAD=∠ADC=40°,
故答案为:40°.
14.(3分)如图,这是一所学校的平面示意图,在同一平面直角坐标系中,教学楼A的坐标为(﹣3,0),实验楼B的坐标为(2,0),则图书馆C的坐标为 (﹣1,﹣3) .
【分析】直接利用已知点坐标进而建立平面直角坐标系,即可得出C点坐标.
【解答】解:如图所示:图书馆C的坐标为(﹣1,﹣3).
故答案为:(﹣1,﹣3).
15.(3分)若(a﹣3)2+=0,则a+b的立方根是 2 .
【分析】根据非负数的性质列式求出a、b的值,然后代入代数式进行计算,再根据立方根的定义解答.
【解答】解:由题意得,a﹣3=0,b﹣5=0,
解得a=3,b=5,
所以,a+b=3+5=8,
所以,a+b的立方根是2.
故答案为:2.
16.(3分)甲和乙同时从A地出发,匀速行走到B地.甲走完一半路程时,乙才走了4千米,乙走完一半路程时,甲已走了9千米.当甲走完全程时,乙未走完的路程还有 4 千米.
【分析】设A,B两地之间的路程为x千米,根据两人的速度之比为定值,即可得出关于x的分式方程,解之经检验后即可得出结论,再结合“甲走完一半路程时,乙才走了4千米”,即可求出结论.
【解答】解:设A,B两地之间的路程为x千米,
依题意,得:=,
化简,得:x2=144,
解得:x1=12,x2=﹣12,
经检验,x1=12,x2=﹣12均为原方程的解,x1=12符合题意,x2=﹣12不符合题意,舍去,
∴x﹣4×2=4.
故答案为:4.
三、解答题:本大题共7小题,满分72分.解答须写出文字说明、推理过程和演算步骤
17.(10分)如图,已知∠AOB=60°,点P在∠AOB的内部,用三角板与量角器作图,并回答问题:
(1)过点P作PC∥OB,交OA于C,并求∠OCP的度数;
(2)过点P作PD⊥OB,垂足为D,连接OP,并比较线段OP与PD的大小.
【分析】(1)连接OP,作∠CPO=∠POD即可,再利用平行线的性质求解即可.
(2)根据垂线段最短即可判断.
【解答】解:(1)如图,直线PC即为所求.
∵PC∥OD,
∴∠OCP+∠AOB=180°,
∵∠AOB=60°,
∴∠OCP=120°.
(2)∵PD⊥OB,
∴PD<OP.
18.(10分)求下列各式中x的值
(1)25x2=4;
(2)(x+1)3=﹣27.
【分析】(1)根据等式的性质,可得平方的形式,根据开方运算,可得答案;
(2)根据开立方运算,可得一元一次方程,根据解方程,可得答案.
【解答】解:(1)方程两边都除以25,得
x2=,
开方得,
x=;
(2)开立方得,
x+1=﹣3,
移项得,
x=﹣4.
19.(10分)解不等式组并把解集在数轴上表示出来.
【分析】分别求出不等式组中两不等式的解集,找出两解集的公共部分确定出不等式组的解集,表示在数轴上即可.
【解答】解:由①得:x>﹣2,
由②得:x≤3,
∴不等式组的解集为﹣2<x≤3,
20.(10分)某家庭记录了使用节水龙头的日用水量样本数据(单位:m3),得到频数分布表如下:
日用水量x
频数
百分比
0≤x<0.1
1
4%
0.1≤x<0.2
2
8%
0.2≤x<0.3
a
20%
0.3≤x<0.4
b
32%
0.4≤x<0.5
6
c
0.5≤x<0.6
3
12%
(1)求a,b,c的值;
(2)在图上补全频数分布直方图;
(3)估计该家庭使用节水龙头100天后,其中日用水量小于0.4m3的天数是多少天?
【分析】(1)根据频数、总数、频率之间的关系进行计算即可;
(2)根据频数分布表,和a、b的值,即可补全频数分布直方图;
(3)样本中日用水量小于0.4m3的天数占调查天数的4%+8%+20%+32%=64%,因此估计100天的64%是4日用水量小于0.4m3的天数占调查天数.
【解答】解:(1)1÷4%=25,a=25×20%=5,b=25×32%=8,c=6÷25=24%,
答:a、b、c的值分别为5,8,24%;
(2)补全频数分布直方图如图所示:
(3)100×(4%+8%+20%+32%)=64(天),
答:该家庭使用节水龙头100天后,其中日用水量小于0.4m3的天数是64天.
21.(10分)如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别是A(﹣5,3),B(﹣3,1),C(﹣2,2).将△ABC先向下平移5个单位长度,然后向右平移6个单位长度,再作关于x轴对称的图形,得到△A1B1C1.
(1)写出点A1,B1,C1的坐标;
(2)在平面直角坐标系xOy中画出△A1B1C1;
(3)求△A1B1C1的面积.
【分析】(1)根据平移规律写出坐标即可.
(2)根据坐标画出图形即可.
(3)利用分割法求出三角形的面积即可.
【解答】解:(1)A1(1,2),B2(3,4),C1(4,3).
(2)如图△A1B1C1即为所求.
(3)=2×3﹣×2×2﹣×1×1﹣×1×3=2.
22.(10分)有大小两种货车,3辆大货车与2辆小货车一次可以运货17吨,5辆大货车与6辆小货车一次可以运货35吨,那么3辆大货车与6辆小货车一次可以运货多少吨?
【分析】设每辆大货车一次可以运货x吨,每辆小货车一次可以运货y吨,根据“3辆大货车与2辆小货车一次可以运货17吨,5辆大货车与6辆小货车一次可以运货35吨”,即可得出关于x,y的二元一次方程组,解之即可得出x,y的值,再将其代入(3x+6y)中即可求出结论.
【解答】解:设每辆大货车一次可以运货x吨,每辆小货车一次可以运货y吨,
依题意,得:,
解得:,
∴3x+6y=3×4+6×=27.
答:3辆大货车与6辆小货车一次可以运货27吨.
23.(12分)如图1,已知∠ACB=80°,点A在直线EF上,点B在直线GH上,且∠CAE+∠CBG=80°.
(1)试判断直线EF与GH的位置关系,并说明理由;
(2)如图2,若点B在直线GH上运动,作∠CAP=2∠CAE,作∠CBP=2∠CBG,试判断∠APB的大小是否会随着点B的运动而发生变化?若不变,求出∠APB的大小;若变化,请说明理由.
【分析】(1)如图1,过点C作CD∥EF,可得∠CAE=∠ACD,由∠ACB=∠ACD+∠BCD=80°,∠CAE+∠CBG=80°.可得∠BCD=∠CBG,得CD∥GH,进而可得直线EF与GH的位置关系;
(2)根据已知条件可得∠CAP+∠CBP=2(∠CAE+∠CBG)=160°,再根据四边形内角和等于360度即可求出∠APB的大小.
【解答】解;(1)直线EF与GH的位置关系是平行,理由如下:
如图1,过点C作CD∥EF,
∴∠CAE=∠ACD,
∵∠ACB=∠ACD+∠BCD=80°,∠CAE+∠CBG=80°.
∴∠BCD=∠CBG,
∴CD∥GH,
∴EF∥GH;
(2)∠APB的大小不会随着点B的运动而发生变化,理由如下:
如图2,∵∠CAP=2∠CAE,∠CBP=2∠CBG,
∴∠CAP+∠CBP=2∠CAE+2∠CBG=2(∠CAE+∠CBG)=2×80°=160°,
∴∠APB=360°﹣∠ACB﹣(∠CAP+∠CBP)=360°﹣80°﹣160°=120°.
所以∠APB的大小为120°.
相关资料
更多








