
数学八年级上册第十二章 全等三角形综合与测试当堂达标检测题
展开时间:100分钟 满分:100分
一.选择题(每小题3分,共30分)
1.已知三角形的两边分别为4和10,则此三角形的第三边可能是( )
A.4B.5C.9D.14
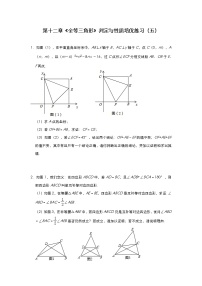
2.如图,BP、CP是△ABC的外角角平分线,若∠P=60°,则∠A的大小为( )
A.30°B.60°C.90°D.120°
3.如图,∠A=20°,∠B=30°,∠C=50°,求∠ADB的度数( )
A.50°B.100°C.70°D.80°
4.将一副三角板按图中的方式叠放,则∠1的度数为( )
A.105°B.100°C.95°D.110°
5.如图,在△ABC中,∠BAC=90°,BD平分∠ABC,CD∥AB交BD于点D,已知∠ACB=34°,则∠D的度数为( )
A.30°B.28°C.26°D.34°
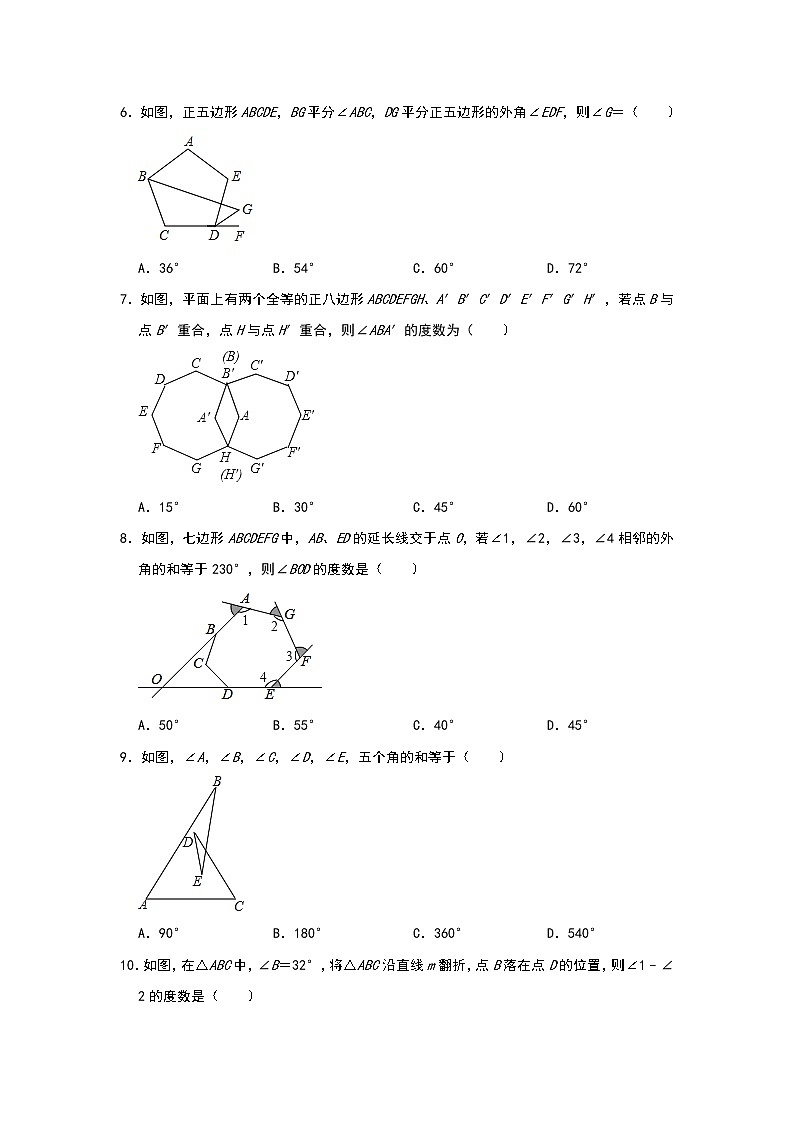
6.如图,正五边形ABCDE,BG平分∠ABC,DG平分正五边形的外角∠EDF,则∠G=( )
A.36°B.54°C.60°D.72°
7.如图,平面上有两个全等的正八边形ABCDEFGH、A′B′C′D′E′F′G′H′,若点B与点B′重合,点H与点H′重合,则∠ABA′的度数为( )
A.15°B.30°C.45°D.60°
8.如图,七边形ABCDEFG中,AB、ED的延长线交于点O,若∠1,∠2,∠3,∠4相邻的外角的和等于230°,则∠BOD的度数是( )
A.50°B.55°C.40°D.45°
9.如图,∠A,∠B,∠C,∠D,∠E,五个角的和等于( )
A.90°B.180°C.360°D.540°
10.如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1﹣∠2的度数是( )
A.32°B.45°C.60°D.64°
二.填空题(每小题4分,共20分)
11.三角形的三边长都是整数,其中两条边长分别是1cm和3cm,则第三条边长是 cm.
12.一个n边形的内角和是它外角和的6倍,则n= .
13.如图,在△ABC中,已知∠B=40°,∠A=30°,则∠BCD= °
14.如图,△ABC中,∠A=55°,将△ABC沿DE翻折后,点A落在BC边上的点A′处.如果∠A′EC=70°,那么∠A′DB的度数为 .
15.如图,六边形ABCDEF的各角都相等,若m∥n,则∠1+∠2= °.
三.解答题(每题10分,共50分)
16.如图,点D,E,G分别是三角形ABC的边AB,AC,BC上的点,点F是线段DG上的点,∠1+∠2=180°,∠C=∠AED.求证∠3=∠B.
请完成证明过程及理由填写.
证明:∵∠1+∠DFE=180°(平角的定义),
∠1+∠2=180°(已知),
∴∠2= (同角的补角相等).
∴EF∥AB( )
∴∠3= ( ).
∵∠C=∠AED(已知),
∴DE∥BC( ).
∴∠B= ( ),
∴∠3=∠B( ).
17.已知:如左图,线段AB、CD相交于点O,连接AD、CB,如右图,在左图的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)在左图中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)在右图中,若∠D=50°,∠B=40°,试求∠P的度数;(写出解答过程)
(3)如果右图中∠D和∠B为任意角,其他条件不变,试写出∠P与∠D、∠B之间数量关系.(直接写出结论)
18.小明在学习过程中,对教材中的一个有趣问题做如下探究:
【习题回顾】已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
【变式思考】如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
【探究廷伸】如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.
19.旧知新意:
我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
尝试探究:
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
初步应用:
(2)如图2,在△ABC纸片中剪去△CDE,得到四边形ABDE,∠1=130°,则∠2﹣∠C= ;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案 .
拓展提升:
(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可接使用,不需说明理由.)
20.将纸片△ABC沿DE折叠使点A落在点A'处
【感知】如图①,点A落在四边形BCDE的边BE上,则∠A与∠1之间的数量关系是 ;
【探究】如图②,若点A落在四边形BCDE的内部,则∠A与∠1+∠2之间存在怎样的数量关系?并说明理由.
【拓展】如图③,点A落在四边形BCDE的外部,若∠1=80°,∠2=24°,则∠A的大小为 .
参考答案
一.选择题
1.解:设此三角形第三边的长为x,则10﹣4<x<10+4,即6<x<14,四个选项中只有9符合条件.
故选:C.
2.证明:∵BP、CP是△ABC的外角的平分线,
∴∠PCB=∠ECB,∠PBC=∠DBC,
∵∠ECB=∠A+∠ABC,∠DBC=∠A+∠ACB,
∴∠PCB+∠PBC=(∠A+∠ABC+∠A+∠ACB)=(180°+∠A)=90°+∠A,
∴∠P=180°﹣(∠PCB+∠PBC)=180°﹣(90°+∠A)=90°﹣∠A=60°,
∴∠A=60°,
故选:B.
3.解:∠BEA是△ACE的外角,
∴∠BEA=∠A+∠C=70°,
∠BDA是△BDE的外角,
∴∠BDA=∠BEA+∠B=100°,
故选:B.
4.解:由图可知,∠2=90°﹣45°=45°,
∴∠1=180﹣45°﹣30°=105°.
故选:A.
5.解:∵∠BAC=90°,∠ACB=34°,
∴∠ABC=180°﹣90°﹣34°=56°,
∵BD平分∠ABC,
∴∠ABD=∠ABC=28°,
∵CD∥AB,
∴∠D=∠ABD=28°,
故选:B.
6.解:如图:
由正五边形ABCDE,BG平分∠ABC,可得∠DPG=90°,
∴∠G+∠EDG=90°,
∵,DG平分正五边形的外角∠EDF,
∴,
∴∠G=90°﹣∠EDG=54°.
故选:B.
7.解:∵两个图形为全等的正八边形,
∴ABA′H为菱形,
∵∠HAB=∠HA′B==135°
∴∠ABA′=180°﹣135°=45°.
故选:C.
8.解:∵∠1、∠2、∠3、∠4的外角的角度和为230°,
∴∠1+∠2+∠3+∠4+230°=4×180°,
∴∠1+∠2+∠3+∠4=490°,
∵五边形OAGFE内角和=(5﹣2)×180°=540°,
∴∠1+∠2+∠3+∠4+∠BOD=540°,
∴∠BOD=540°﹣490°=50°,
故选:A.
9.解:如图所示,延长BE,交AC于点F,CD与BE交于点G,
∵∠CGF=∠D+∠DEG,∠BFC=∠A+∠B,
∴∠A+∠B+∠C+∠D+∠DEG=∠CGF+∠BFC+C=180°.
故选:B.
10.解:如图所示:
由折叠的性质得:∠D=∠B=32°,
根据外角性质得:∠1=∠3+∠B,∠3=∠2+∠D,
∴∠1=∠2+∠D+∠B=∠2+2∠B=∠2+64°,
∴∠1﹣∠2=64°.
故选:D.
二.填空题(共5小题)
11.解:∵两条边长分别是1cm和3cm,
∴第三边的取值范围是2<第三边<4,
∵三边均为整数,
∴第三边的长为3cm,
故答案为:3.
12.解:多边形的外角和是360°,多边形的内角和是180°•(n﹣2),根据题意得:
180•(n﹣2)=360×6,
解得n=14.
故答案为:14.
13.解:∵∠BCD=∠A+∠B,∠A=30°,∠B=40°,
∴∠BCD=70°,
故答案为70.
14.解:由翻折的性质可知:∠ADE=∠EDA′,∠AED=∠A′ED=(180°﹣70°)=55°,
∵∠A=55°,
∴∠ADE=∠EDA′=180°﹣55°﹣55°=70°,
∴∠A′DB=180°﹣140°=40°,
故答案为40°.
15.解:延长DC,交直线n于点G,
∵六边形ABCDEF的各角都相等,
∴AF∥DC,
∴∠2=∠3,
又∵m∥n,
∴∠3+∠4=180°,
∵∠4=∠1,
∴∠1+∠2=180°,
故答案为:180.
三.解答题(共5小题)
16.证明:∵∠1+∠DFE=180°(平角的定义),
∠1+∠2=180°(已知),
∴∠2=∠DFE(同角的补角相等).
∴EF∥AB(内错角相等两直线平行)
∴∠3=∠ADE(两直线平行内错角相等).
∵∠C=∠AED(已知),
∴DE∥BC(同位角相等两直线平行2).
∴∠B=∠ADE(两直线平行同位角相等),
∴∠3=∠B(等量代换),
故答案为:∠DFE,内错角相等两直线平行,两直线平行内错角相等,同位角相等两直线平行,∠ADE,两直线平行同位角相等,等量代换.
17.解:(1)∵∠A+∠D+∠AOD=∠B+∠C+∠BOC=180°,∠AOD=∠BOC,
∴∠A+∠D=∠B+∠C,
故答案为∠A+∠D=∠B+∠C.
(2)由(1)得,∠1+∠D=∠3+∠P,∠2+∠P=∠4+∠B,
∴∠1﹣∠3=∠P﹣∠D,∠2﹣∠4=∠B﹣∠P,
又∵AP、CP分别平分∠DAB和∠BCD,
∴∠1=∠2,∠3=∠4,
∴∠P﹣∠D=∠B﹣∠P,
即2∠P=∠B+∠D,
∴∠P=(50°+40°)÷2=45°.
(3)由(2)可知:2∠P=∠B+∠D.
18.【习题回顾】证明:∵∠ACB=90°,CD是高,
∴∠B+∠CAB=90°,∠ACD+∠CAB=90°,
∴∠B=∠ACD,
∵AE是角平分线,
∴∠CAF=∠DAF,
∵∠CFE=∠CAF+∠ACD∠CEF=∠DAF+∠B,
∴∠CEF=∠CFE;
【变式思考】∠CEF=∠CFE
证明:∵AF为∠BAG的角平分线,
∴∠GAF=∠DAF,
∵CD为AB边上的高,
∴∠ACB=90°,
∴∠ADF=∠ACE=90°,又∵∠CAE=∠GAF,
∴∠CEF=∠CFE;
【探究思考】∠M+∠CFE=90°,
证明:∵C、A、G三点共线 AE、AN为角平分线,
∴∠EAN=90°,又∵∠GAN=∠CAM,
∴∠M+∠CEF=90°,
∵∠CEF=∠EAB+∠B,∠CFE=∠EAC+∠ACD,∠ACD=∠B,
∴∠CEF=∠CFE,
∴∠M+∠CFE=90°.
19.解:(1)∠DBC+∠ECB
=180°﹣∠ABC+180°﹣∠ACB
=360°﹣(∠ABC+∠ACB)
=360°﹣(180°﹣∠A)
=180°+∠A;
(2)∵∠1+∠2=∠180°+∠C,
∴130°+∠2=180°+∠C,
∴∠2﹣∠C=50°;
(3)∠DBC+∠ECB=180°+∠A,
∵BP、CP分别平分外角∠DBC、∠ECB,
∴∠PBC+∠PCB=(∠DBC+∠ECB)=(180°+∠A),
在△PBC中,∠P=180°﹣(180°+∠A)=90°﹣∠A;
即∠P=90°﹣∠A;
故答案为:50°,∠P=90°﹣∠A;
(4)延长BA、CD于Q,
则∠P=90°﹣∠Q,
∴∠Q=180°﹣2∠P,
∴∠BAD+∠CDA=180°+∠Q,
=180°+180°﹣2∠P,
=360°﹣2∠P.
20.解:(1)如图①,∠1=2∠A.
理由如下:由折叠知识可得:∠EA′D=∠A;
∵∠1=∠A+∠EA′D,
∴∠1=2∠A.
(2)如图②,2∠A=∠1+∠2.
理由如下:∵∠1+∠A′DA+∠2+∠A′EA=360°,
∠A+∠A′+∠A′DA+∠A′EA=360°,
∴∠A′+∠A=∠1+∠2,
由折叠知识可得:∠A=∠A′,
∴2∠A=∠1+∠2.
(3)如图③,
∵∠1=∠DFA+∠A,∠DFA=∠A′+∠2,
∴∠1=∠A+∠A′+∠2=2∠A+∠2,
∴2∠A=∠1﹣∠2=56°,
解得∠A=28°.
故答案为:∠1=2∠A;28°.
人教版八年级上册12.1 全等三角形同步训练题: 这是一份人教版八年级上册12.1 全等三角形同步训练题,文件包含八年级数学上册第十二章全等三角形单元培优训练原卷版docx、八年级数学上册第十二章全等三角形单元培优训练解析版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
初中数学人教版八年级上册第十二章 全等三角形综合与测试综合训练题: 这是一份初中数学人教版八年级上册第十二章 全等三角形综合与测试综合训练题,共13页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2021学年第十二章 全等三角形综合与测试单元测试同步训练题: 这是一份2021学年第十二章 全等三角形综合与测试单元测试同步训练题,共8页。试卷主要包含了选择题等内容,欢迎下载使用。