初中12.2 三角形全等的判定第3课时学案

这是一份初中12.2 三角形全等的判定第3课时学案，共4页。学案主要包含了预习导学，合作探究等内容，欢迎下载使用。



1．理解和掌握全等三角形判定方法3——“ASA”，判定方法4——“AAS”；能运用它们判定两个三角形全等．


2．能把证明一对角或线段相等的问题，转化为证明它们所在的两个三角形全等．





阅读教材P39～41，完成预习内容．


知识探究


1．两角和它们的夹边分别相等的两个三角形________(可以简写成“角边角”或“________”)．


2．两角和其中一个角的对边分别相等的两个三角形________(可以简写成“角角边”或“________”)．


3．试总结全等三角形的判定方法，师生共同总结．


三角形全等的条件至少需要三对相等的元素(其中至少需要一条边相等)．


自学反馈


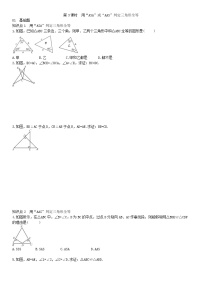
1．能确定△ABC≌△DEF的条件是( )


A．AB＝DE，BC＝EF，∠A＝∠E


B．AB＝DE，BC＝EF，∠C＝∠E


C．∠A＝∠E，AB＝EF，∠B＝∠D


D．∠A＝∠D，AB＝DE，∠B＝∠E


2．如图，已知△ABC的六个元素，则下面甲、乙、丙三个三角形中，和△ABC全等的图形是( )








A．甲和乙 B．乙和丙 C．只有乙 D．只有丙


3．AD是△ABC的角平分线，作DE⊥AB于E，DF⊥AC于F，下列结论错误的是( )


A．DE＝DF B．AE＝AF


C．BD＝CD D．∠ADE＝∠ADF


应用AAS证三角形全等时应注意边是对应角的对边．


4．阅读下题及一位同学的解答过程：如图，AB和CD相交于点O，且OA＝OB，∠A＝∠C.那么△AOD与△COB全等吗？若全等，试写出证明过程；若不全等，请说明理由．





解：△AOD≌△COB.


证明：在△AOD和△COB中，


eq \b\lc\{(\a\vs4\al\c1(∠A＝∠C（已知），,OA＝OB（已知），,∠AOD＝∠COB（对顶角相等），))


∴△AOD≌△COB(ASA)．


问：这位同学的回答及证明过程正确吗？为什么？


应用ASA证全等三角形时应注意边是对应角的夹边．








活动1 小组讨论


例1 已知：如图，在△MPN中，H是高MQ和NR的交点，且MQ＝NQ.求证：HN＝PM.





证明：∵MQ⊥PN，


∴∠MQP＝∠MQN＝90°.


∵NR⊥MP，∴∠MRN＝90°.





∴∠RMH＋∠RHM＝∠QHN＋∠QNH＝90°.


又∵∠RHM＝∠QHN，∴∠PMQ＝∠QNH.


在△PMQ与△HNQ中，∵∠MQP＝∠NQH＝90°，MQ＝NQ，∠PMQ＝∠QNH，∴△PMQ≌△HNQ.∴HN＝PM.


有直角三角形就有互余的角，利用同角(等角)的余角相等是证角相等的常用方法．


例2 已知：如图，AB⊥AE，AD⊥AC，∠E＝∠B，DE＝CB.


求证：AD＝AC.





证明：∵AB⊥AE，AD⊥AC，


∴∠CAD＝∠BAE＝90°.


∴∠CAD＋∠BAD＝∠BAE＋∠BAD.∴∠CAB＝∠DAE.


在△ABC与△AED中，


∵∠CAB＝∠DAE，∠B＝∠E，CB＝DE，


∴△ABC≌△AED.∴AD＝AC.


利用角的和证角相等．


活动2 跟踪训练


1．已知：如图，PM＝PN，∠M＝∠N.求证：AM＝BN.





2．P41页练习1、2题．


善于挖掘隐藏条件“公共边、公共角、对顶角”等．


活动3 课堂小结


1．本节内容是已知两个角和一条边对应相等得全等，三个角对应相等不能确定全等．


2．三角形全等的判定和全等三角形的性质常在一起进行综合应用，有时还得反复用两次或两次以上，从而达到解决问题的目的．





【预习导学】


知识探究


1．全等 ASA 2.全等 AAS


自学反馈


1．D 2.B 3.C 4.略．


【合作探究】


活动2 跟踪训练


1．略． 2.略．