北师大版九年级上册2 用频率估计概率教案

这是一份北师大版九年级上册2 用频率估计概率教案，共2页。



3.2 用频率估计概率





1．借助实验，体会随机事件在每一次实验中发生与否具有不确定性．


2．通过操作，体验重复实验的次数与事件发生的频率之间的关系，能从频率值角度估计事件发生的概率．(重点)


3．懂得开展实验、设计实验，通过实验数据探索规律，并从中学会合作与交流．





阅读教材P69～70，完成下列问题：


自学反馈


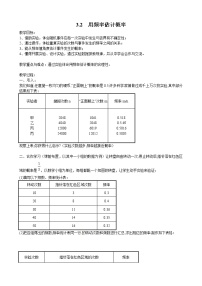
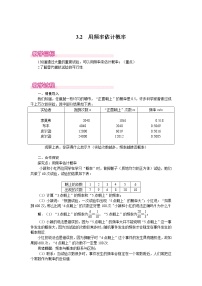
让转盘自由转动一次，停止转动后，指针落在红色区域的概率是eq \f(1,3)，以数学小组为单位，每组都配一个如题的转盘，让学生动手实验来验证：


(1)填写以下频数、频率统计表：


(2)把各组得出的频数，频率统计表同一行的转动次数和频数进行汇总，求出相应的频率，制作如下表格：


(3)根据上面的表格，画出频率分布折线图．


(4)议一议：频率与概率有什么区别和联系？随着重复实验次数的不断增加，频率的变化趋势如何？


结论：从上面的试验可以看到：当重复实验的次数大量增加时，事件发生的频率就稳定在相应的概率附近．因此，我们可以通过大量重复实验，用一个事件发生的频率来估计这一事件发生的概率．





活动1 小组讨论


例1 50个同学中有2个同学的生日相同，不能说明50个同学中有2个同学生日相同的概率是1；如果50个同学中没有2个同学生日相同，不能说明其相应概率是0.(填“能”或“不能”)因此我们只能通过设计方案，通过重复试验的方法来估计50人中有2人生日相同的概率．


收集数据，进行试验，统计结果．


通过以上试验得知50个同学中，有2个学生的生日相同的可能性比较小(填“大”或小)．


小组合作完成教材P70中的“想一想”．


尽可能多的重复试验，方能用频率估计概率．


活动2 跟踪训练


1．某人在做掷硬币试验时，投掷 m次，正面朝上有n次(即正面朝上的频率是p＝eq \f(n,m))．则下列说法中正确的是( )


A．p一定等于eq \f(1,2)


B．p一定不等于eq \f(1,2)


C．多投一次，p更接近eq \f(1,2)


D．投掷次数逐渐增加，p稳定在eq \f(1,2)附近[来源]


2．在一个不透明的布袋中，红色、黑色、白色的玻璃球共有40个，除颜色外其他完全相同．小李通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在15%和45%，则口袋中白色球的个数很可能是( )


A．6 B．16


C．18 D．24


3．甲、乙两名同学在一次用频率去估计概率的实验中统计了某一结果出现的频率，绘出的统计图如图所示，则符合这一结果的试验可能是( )[来源:学&科&网]


A．掷一枚正六面体的骰子，出现1点的概率


B．从装有2个白球和1个红球的袋子中任取一球，取到红球的概率


C．抛一枚硬币，出现正面的概率


D．任意写一个整数，它能被2整除的概率





4．某人把50粒黄豆染色后与一袋黄豆充分混匀，接着抓出100粒黄豆，数出其中有10粒黄豆被染色，则这袋黄豆原来约有________粒．


5．A市大约有100万常住人口，随机抽查了2 000人，具有大学以上学历的有120人，则在A市随机调查一个人，他具有大学以上学历的概率约是________．


活动3 课堂小结


1．可以通过多次试验，用一个事件发生的频率来估计这一事件发生的概率．


2．当实验次数很大时，频率比较稳定，稳定在相应的概率附近．


3．(在一定合理性条件下)假设试验频率＝理论概率，列出方程求解，得要求的未知数值；








【预习导学】


自学反馈


略


【合作探究】


活动2 跟踪训练


1．D 2.B 3.B 4.450 5.6%转动次数
指针落在红色区域次数
频率
10
20
30
40
50
实验次数
指针落在红色区域的次数
频率
80
160
240
320
400
试验次数
有两人生日相同的频数
有两人生日相同的频率