




北师大版九年级上册2 矩形的性质与判定说课ppt课件
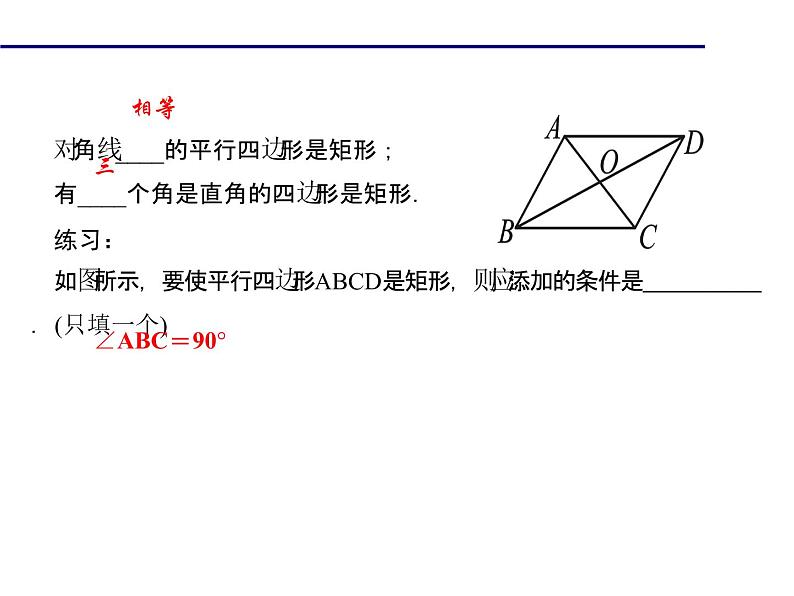
展开对角线____的平行四边形是矩形;有____个角是直角的四边形是矩形.练习:如图所示,要使平行四边形ABCD是矩形,则应添加的条件是 .(只填一个)
1.四边形ABCD的对角线AC,BD相交于点O,下列各条件中,能判断四边形ABCD是矩形的是( )A.AO=CO,BO=DOB.AO=BO=CO=DOC.AC=BD,AO=COD.AO=CO,BO=DO,AC⊥BD
2.下列关于矩形的说法中正确的是( )A.对角线相等的四边形是矩形B.对角线互相平分的四边形是矩形C.矩形的对角线互相垂直平分D.矩形的对角线相等且互相平分
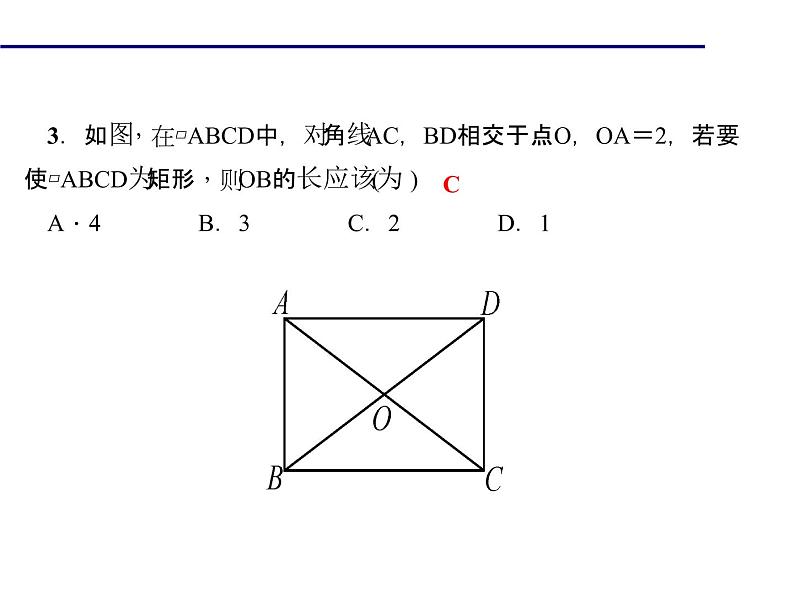
3.如图,在▱ABCD中,对角线AC,BD相交于点O,OA=2,若要使▱ABCD为矩形,则OB的长应该为( )A.4 B.3 C.2 D.1
5.(易错题)如图,在△ABC中,AB=AC,将△ABC绕点C旋转180°得到△FEC,连接AE,BF.当∠ACB为____度时,四边形ABFE为矩形.
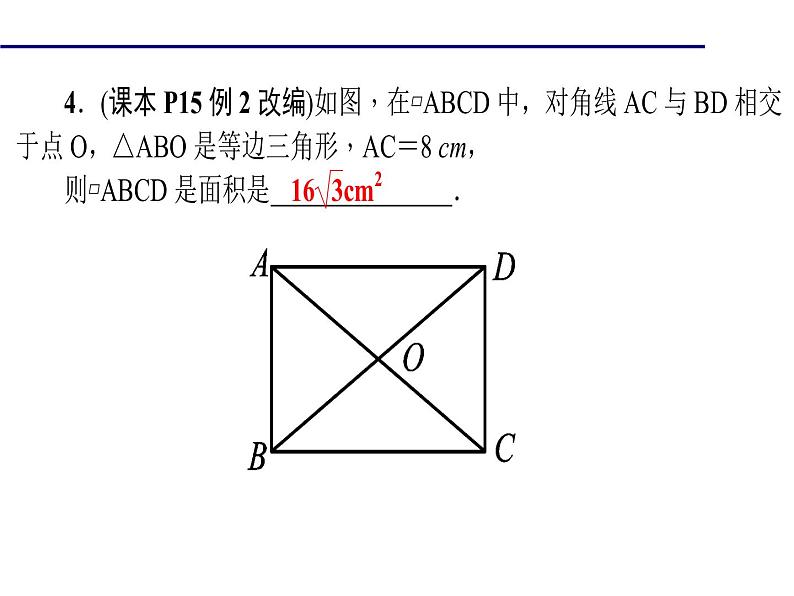
6.如图,在▱ABCD中,对角线AC,BD相交于点O,且∠OBC=∠OCB.求证:四边形ABCD是矩形.证明OB=OC,得到AC=BD即可
7.在数学活动课上,同学们判断一个四边形门框是否为矩形.下面是某学习小组4位同学拟定的方案,其中正确的是( )A.测量对角线是否互相平分B.测量两组对边是否分别相等C.测量其中三个角是否都为直角D.测量对角线是否相等
8.如图,直角∠AOB内的一点P到这个角的两边的距离之和为6,则图中四边形的周长为____.9.如图,点M是矩形ABCD的边AD的中点,点P为BC上一点,PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足条件 时,四边形PEMF为矩形.
10.已知▱ABCD的对角线交于点O,分别添加下列条件:①∠ABC=90°;②AC⊥BD;③AC=BD;④OA=OD.能使▱ABCD是矩形的条件的序号是 .
11.如图,点E,F分别为△ABC的边BC,CA的中点,延长EF到点D,使得DF=EF,连接DA,DC,AE.(1)求证:四边形ABED是平行四边形;(2)若AB=AC,求证:四边形AECD是矩形.
(1)∵AF=CF,DF=EF,∴四边形AECD是平行四边形,∴AD∥BC,AD=CE,又∵BE=CE,∴AD=BE,∴四边形ABED是平行四边形(2)∵AB=AC,BE=CE,∴AE⊥BC,∴∠AEC=90°,∴▱AECD是矩形
(1)∵BE⊥AC,DF⊥AC,∴∠BEO=∠DFO=90°,∵点O是EF的中点,∴OE=OF,又∵∠BOE=∠DOF,∴△BOE≌△DOF(ASA)
13.(2016·吉林)如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.求证:四边形AODE是矩形.∵DE∥AC,AE∥BD,∴四边形AODE是平行四边形.∵四边形ABCD是菱形,∴AC⊥BD,∴∠AOD=90°.∴四边形AODE是矩形
14.(阿凡题:1071404)(教材例4变式题)如图,在△ABC中,点O是边AC上一个动点,过点O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.连接AE,AF.(1)求证:OE=OF;(2)若CE=12,CF=5,求OC的长;(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
(1)∵CF平分∠ACD,且MN∥BD,∴∠ACF=∠FCD=∠CFO.∴OF=OC.同理可证OC=OE.∴OE=OF
初中数学北师大版九年级上册2 矩形的性质与判定优秀ppt课件: 这是一份初中数学北师大版九年级上册2 矩形的性质与判定优秀ppt课件,文件包含第2课时矩形的判定pptx、第2课时矩形的判定教案及反思doc、活动框架mp4等3份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
北师大版九年级上册2 矩形的性质与判定优质课件ppt: 这是一份北师大版九年级上册2 矩形的性质与判定优质课件ppt,文件包含12矩形的性质与判定第2课时教学课件pptx、第一章特殊平行四边形12矩形的性质与判定第2课时教案内含练习docx等2份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
北师大版九年级上册2 矩形的性质与判定习题课件ppt: 这是一份北师大版九年级上册2 矩形的性质与判定习题课件ppt,共27页。PPT课件主要包含了①③④等内容,欢迎下载使用。













