



北师大版九年级上册2 矩形的性质与判定授课ppt课件
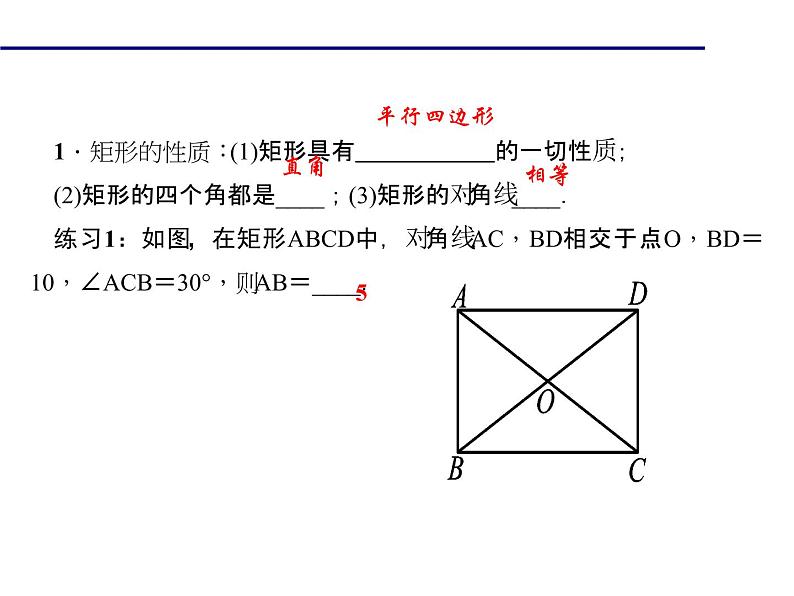
展开1.矩形的性质:(1)矩形具有 的一切性质;(2)矩形的四个角都是____;(3)矩形的对角线____.练习1:如图,在矩形ABCD中,对角线AC,BD相交于点O,BD=10,∠ACB=30°,则AB=____.
2.矩形的判定:(1)有一个角是____的平行四边形是矩形;(2)有三个角是____的 是矩形;(3)对角线____的 是矩形.
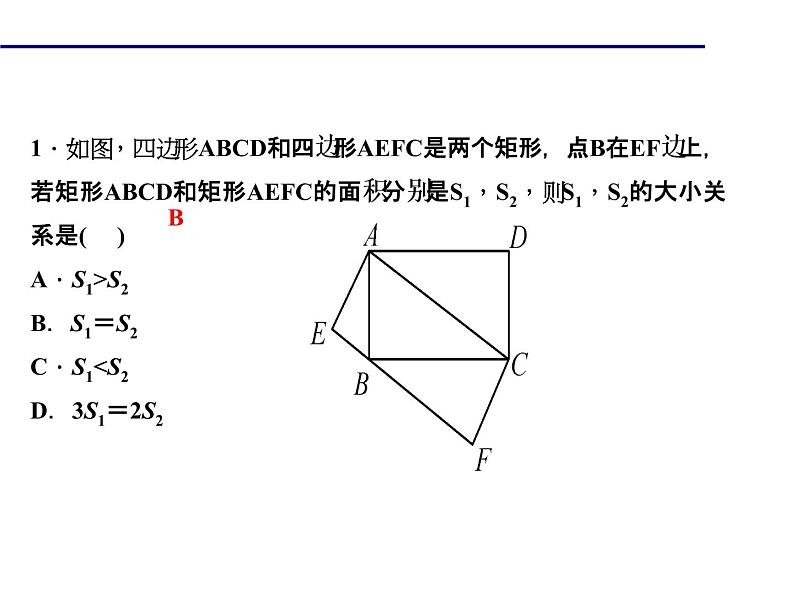
1.如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1,S2,则S1,S2的大小关系是( )A.S1>S2 B.S1=S2C.S1
3.(2016·天津)如图,把一张矩形纸片ABCD沿对角线AC折叠,点B的对应点为B′,AB′与DC相交于点E,则下列结论一定正确的是( )A.∠DAB′=∠CAB′B.∠ACD=∠B′CDC.AD=AED.AE=CE
4.在四边形ABCD中,AC和BD的交点为点O,下列条件中不能判定四边形ABCD为矩形的是( )A.AB=CD,AD=BC,AC=BDB.AO=CO,BO=DO,∠A=90°C.∠A=∠C,∠B+∠C=180°,∠AOB=∠BOCD.AB∥CD,AB=CD,∠A=90°
8.在四边形ABCD中,对角线AC,BD交于点O,从①AB=CD;②AB∥CD;③OA=OC;④OB=OD;⑤AC=BD;⑥∠ABC=90°.这六个条件中,可选取三个推出四边形ABCD是矩形,如①②⑤⇒四边形ABCD是矩形,请再写出符合要求的两个:①②⑥⇒四边形ABCD是矩形;③④⑤⇒四边形ABCD是矩形;(另外③④⑥,②③⑤⇒四边形ABCD是矩形).
9.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.(1)求证:BD=BE;(2)若∠DBC=30°,BO=4,求四边形ABED的面积.
(1)∵四边形ABCD是矩形,∴BD=AC,AB∥CE,又∵BE∥AC,∴四边形ABEC是平行四边形,∴BE=AC,∴BD=BE
10.如图,在矩形ABCD中,AB=2,BC=4,对角线AC的垂直平分线分别交AD,AC于点E,O,连接CE,则CE的长为( )A.3 B.3.5C.2.5 D.2.8
12.如图,在矩形ABCD中,两条对角线AC,BD相交于点O,点E是AC上的一点,且BO=2AE,∠AOD=120°,求证:BE⊥AC.证明△AOB为等边三角形,点E是OA的中点即可
14.如图,四边形ABCD是菱形,点E,F,G,H分别是AD,AB,BC,CD的中点.(1)求证:四边形EFGH是矩形;(2)若菱形ABCD的面积是50,求四边形EFGH的面积.
15.如图,点D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.(1)求证:CD=AN;(2)若∠AMD=2∠MCD,求证:四边形ADCN是矩形.
(1)证△AMD≌△CMN得AD=CN,又∵AD∥CN,∴四边形ADCN是平行四边形,∴CD=AN (2)∵∠AMD=2∠MCD,∠AMD=∠MCD+∠MDC,∴∠MCD=∠MDC,∴MD=MC,由(1)知四边形ADCN是平行四边形,∴MD=MN=MA=MC,∴AC=DN,∴▱ADCN是矩形
(1)∵四边形ABCD是矩形,∴AD∥BC,∴∠ANM=∠CMN,由折叠知∠CNM=∠ANM,∴∠CNM=∠CMN,∴CN=CM
数学北师大版2 矩形的性质与判定课文内容课件ppt: 这是一份数学北师大版2 矩形的性质与判定课文内容课件ppt,共10页。PPT课件主要包含了创设情境导入新课,探究新知经历过程,想一想,巩固练习深化提高等内容,欢迎下载使用。
初中数学北师大版九年级上册第一章 特殊平行四边形2 矩形的性质与判定完美版课件ppt: 这是一份初中数学北师大版九年级上册第一章 特殊平行四边形2 矩形的性质与判定完美版课件ppt,文件包含第3课时矩形的性质与判定的综合运用pptx、第3课时矩形的性质与判定的运用教案及反思doc等2份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
北师大版九年级上册2 矩形的性质与判定教课内容ppt课件: 这是一份北师大版九年级上册2 矩形的性质与判定教课内容ppt课件,共17页。PPT课件主要包含了一个内角是直角,几何画板,对边平行且相等,对角相等邻角互补,对角线互相平分,是中心对称图形,∠B90°,∠ABC90°,又∵BEED,∴EAEC等内容,欢迎下载使用。













