数学北师大版第五章 二元一次方程组7 用二元一次方程组确定一次函数表达式学案

这是一份数学北师大版第五章 二元一次方程组7 用二元一次方程组确定一次函数表达式学案，共5页。

基础导练


1．一次函数y＝7－4x和y＝1－x的图象的交点坐标为___________，则方程组 SKIPIF 1 < 0 的解为___________．


2．已知 SKIPIF 1 < 0 是方程组 SKIPIF 1 < 0 的解，那么由两个方程得到的一次函数y＝___________和y＝___________的交点坐标是 ．


3．方程组 SKIPIF 1 < 0 解的情况是________，则一次函数y＝2－2x与y＝5－2x图象之间的位置关系是________．


4．若一次函数 SKIPIF 1 < 0 和一次函数 SKIPIF 1 < 0 的交点坐标为（m，8）．则m＝ ，b＝ ．


5．如果 SKIPIF 1 < 0 是方程组 SKIPIF 1 < 0 的解，则一次函数y＝mx＋n的解析式为 ．


6．在图中的两直线l1、l2的交点坐标可以看作方程组 的解．


2


4


6


-4


O


x


y


l1





千米


4


2


20


60


分





6题图 7题图


7．已知A、B两地相距4千米，上午8：00甲从A地出发步行到B地，8：20乙从B地出发骑自行车到A地，甲、乙两人离A地的距离（千米）与时间（分）的关系如图，由图中的信息可知，乙出发_______分他们所走的路程一样．


8．某航空公司规定，乘客可以免费携带一定质量的行李，但超过该质量则需购买行李票，且行李费y（元）是行李质量x（千克）的一次函数，现知王芳带了30千克的行李，买了行李票50元．李刚带了40千克的行李，买了行李票100元．则这家航空公司规定旅客最多可免费携带多少千克的行李？























9．用图象法解下列方程组：


（1） SKIPIF 1 < 0 （2） SKIPIF 1 < 0























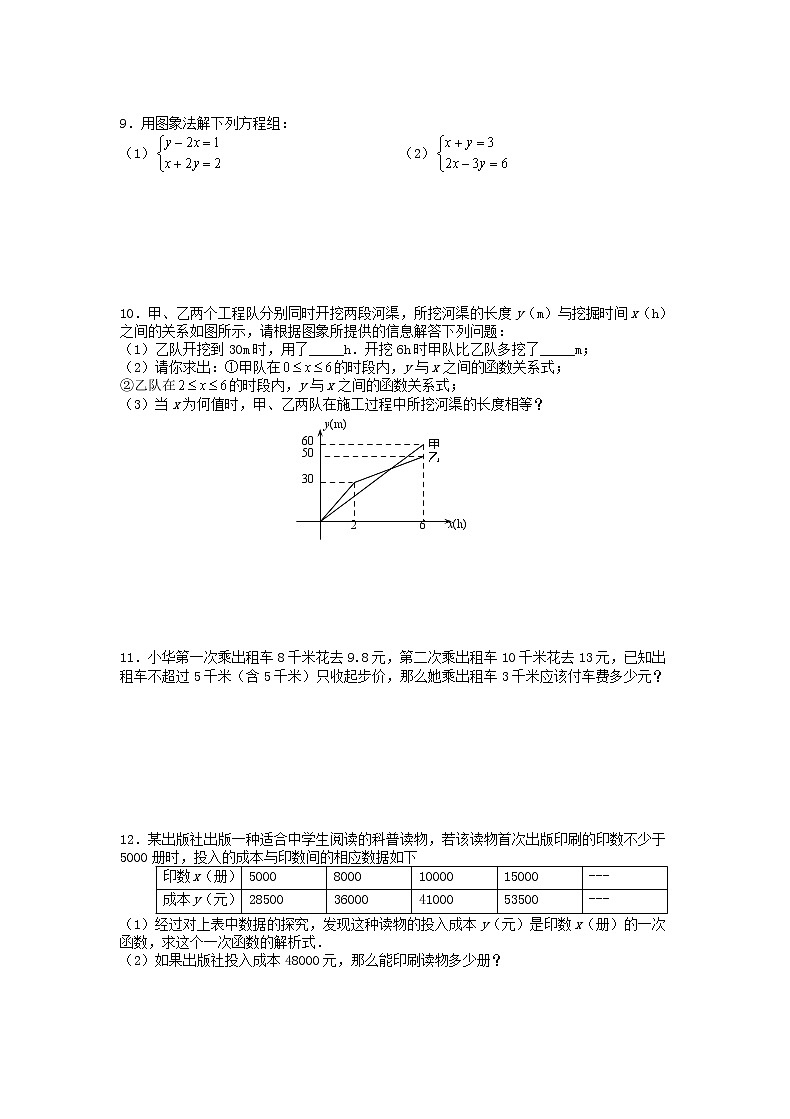
10．甲、乙两个工程队分别同时开挖两段河渠，所挖河渠的长度y（m）与挖掘时间x（h）之间的关系如图所示，请根据图象所提供的信息解答下列问题：


（1）乙队开挖到30m时，用了_____h．开挖6h时甲队比乙队多挖了_____m；


（2）请你求出：①甲队在 SKIPIF 1 < 0 的时段内，y与x之间的函数关系式；


②乙队在 SKIPIF 1 < 0 的时段内，y与x之间的函数关系式；


（3）当x为何值时，甲、乙两队在施工过程中所挖河渠的长度相等？


6


2


O


x(h)


y(m)


30


60


乙


甲


50




















11．小华第一次乘出租车8千米花去9.8元，第二次乘出租车10千米花去13元，已知出租车不超过5千米（含5千米）只收起步价，那么她乘出租车3千米应该付车费多少元？


























12．某出版社出版一种适合中学生阅读的科普读物，若该读物首次出版印刷的印数不少于5000册时，投入的成本与印数间的相应数据如下


（1）经过对上表中数据的探究，发现这种读物的投入成本y（元）是印数x（册）的一次函数，求这个一次函数的解析式．


（2）如果出版社投入成本48000元，那么能印刷读物多少册？

















能力提升


13．如图：过点A的一次函数的图象与正比例函数y＝2x的图象交于点B，能表示这个一次函数图象的方程是（ ）


A．2x－y＋3＝0B．x－y－3＝0C．2y－x＋3＝0D．x＋y－3＝0


A








y＝2x


B


x


1


0


3


y


SKIPIF 1 < 0


13题图 15题图


14．已知一次函数y1＝－ SKIPIF 1 < 0 x－4，与y2＝2ax＋4a＋b


（1）求a、b为何值时，两函数的图象重合？


（2）如果它们图象的交点为 P（－1，3），试确定方程组 SKIPIF 1 < 0 的解并求a、b的值？

















15．如图，l甲、l乙分别表示甲走路与乙骑自行车（在同一条路上）行走的路程s与时间t的关系，观察图象并回答下列问题：


（1）乙出发时，与甲相距________千米；


（2）走了一段路程后，乙的自行车发生故障，停下来修理，修车的时间为______小时；


（3）乙从出发起，经过______小时与甲相遇；


（4）甲行走的路程s（千米）与时间t（时）之间的函数关系是 ；


（5）如果乙的自行车不出现故障，那么乙出发后经过______时与甲相遇，相遇处离乙的出发点______千米，并在图中标出其相遇点．


16．某企业有甲、乙两个长方体的蓄水池，将甲池中的水以每小时6立方米的速度注入乙池，甲、乙两个蓄水池中水的深度y（米）与注水时间x（时）之间的函数图像如图所示，结合图像回答下列问题：


（1）分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数关系式；


（2）求注水多长时间甲、乙两个蓄水池水的深度一样；


（3）求注水多长时间甲、乙两个蓄水池的蓄水量相同．


O


3


x（小时）


1


2


4


y(米)























17．下图表示甲、乙两名选手在一次自行车越野赛中，路程y（千米）随时间x（分）变化的图象．根据图象回答问题：


（1）求比赛开始多少分钟时，两人第一次相遇？


（2）求这次比赛全程是多少千米？


（3）求比赛开始多少分钟时，两人第二次相遇？

















18阿基米德与金冠之迷


相传，2000多年前古希腊的亥尼洛国王做了一顶金王冠．但是，这个国王相当多疑，他怀疑工匠用银子偷换了王冠中的金子．国王便要求阿基米德查出王冠是否是由纯金制造的，而且提出要求不能损坏王冠．阿基米德捧着这顶王冠整日苦苦思索却找不到问题的答案．有一天，阿基米德去浴室洗澡，当他跨入盛满水的浴桶后，随着身子进入浴桶，他发现有一部分水从浴桶中溢出，阿基米德看到这个现象头脑中马上意识到了什么，便高呼：“我找到了！我找到了！”，他的脑海中顿时闪现：不是可以通过对比金冠和与金冠重量相当的金块与银块的排水量来测量吗? 他忘记了自己还光着身子，便从浴桶中一跃而出奔向王宫．一路上高呼：“我找到了！我找到了！”他这一声高呼便宣告了阿基米德原理的诞生，解决了王冠之迷．


有资料这样描写阿基米德鉴定金冠的过程：因为金冠是12磅，于是取来12磅的纯金和12磅的纯银，称它们在水中的质量分别是 SKIPIF 1 < 0 磅 SKIPIF 1 < 0 磅，再称金冠在水中的质量是 SKIPIF 1 < 0 磅，于是算出金冠中是否掺了银子以及掺了多少银子．


聪明的你能说明其中所蕴涵的数学道理吗？






































参考答案


1．（2. －1）， SKIPIF 1 < 0 2． SKIPIF 1 < 0 ，y＝－2x＋8，（2，4） 3．无解，平行 4．5；13 5．y＝x＋2 6． SKIPIF 1 < 0 7．10分 8． SKIPIF 1 < 0 ，则当 SKIPIF 1 < 0 时， SKIPIF 1 < 0 ．所以旅客最多可免费携带20千克的行李 9．略 10．（1）2，10；（2）y＝10x， y＝5x＋20；（3）x＝4 11．5元 12．（1）y＝2.5x＋16000；（2）12800 册 13．B 14．（1）若两函数图象重合，需使 SKIPIF 1 < 0 ，解得 SKIPIF 1 < 0 ．∴a＝1，b＝－8时，两函数的图象重合；（2）若两直线相交于点（－1，3），则 SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 15．（1）10；（2）1；（3）3；（4） SKIPIF 1 < 0 ；（5） SKIPIF 1 < 0 ， SKIPIF 1 < 0


16．（1） SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；（2）交点 SKIPIF 1 < 0 ；（3）设甲底面积a，乙底面积b，t小时它们的蓄水量相同．由题得：2a＝3×6，a＝9；（4－1）b＝3×6，b＝6；9 SKIPIF 1 < 0 ．


17．（1） SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；（2） SKIPIF 1 < 0 ， SKIPIF 1 < 0 ；（3） SKIPIF 1 < 0 ， SKIPIF 1 < 0


18.略





印数x（册）
5000
8000
10000
15000
---
成本y（元）
28500
36000
41000
53500
---