





初中数学浙教版八年级上册2.4 等腰三角形的判定定理课文配套ppt课件
展开第2章 特殊三角形2.4 等腰三角形的性质定理
2、等腰三角形的两个底角相等.
(在同一个三角形中,等边对等角)
1、等腰三角形的两腰相等.
3、等腰三角形三线合一
顶角平分线、底边上的中线 和底边上的高
等腰三角形的判定方法:
1、有两边相等的三角形是等腰三角形。(定义)
两个角相等的三角形会是等腰三角形吗?
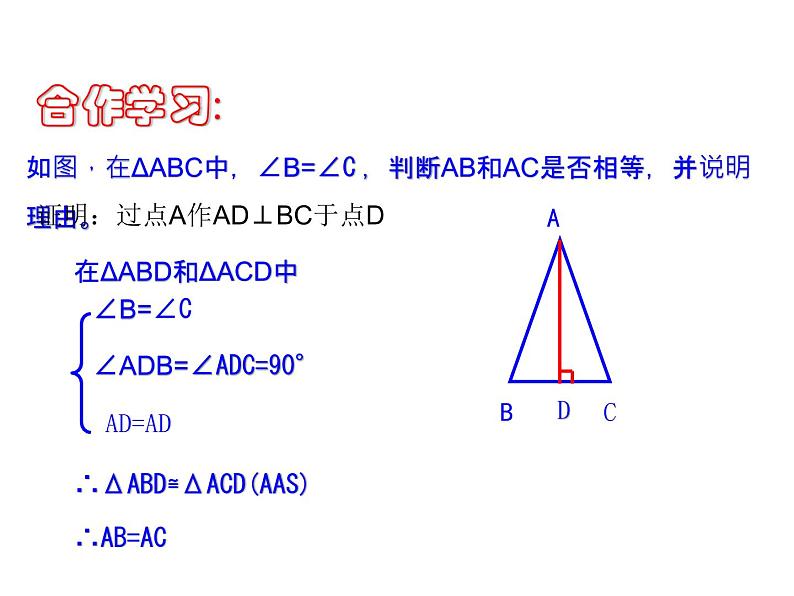
如图,在ΔABC中,∠B=∠C,判断AB和AC是否相等,并说明理由。
在ΔABD和ΔACD中
∴ΔABD≌ΔACD(AAS)
证明:过点A作AD⊥BC于点D
“在同一个三角形中,等角对等边。”
2、如果一个三角形有两个角相等,那么这个三角形是等腰三角形.
“在同一个三角形中, 等边对等角。”
1、有两边相等的三角形是等腰三角形。
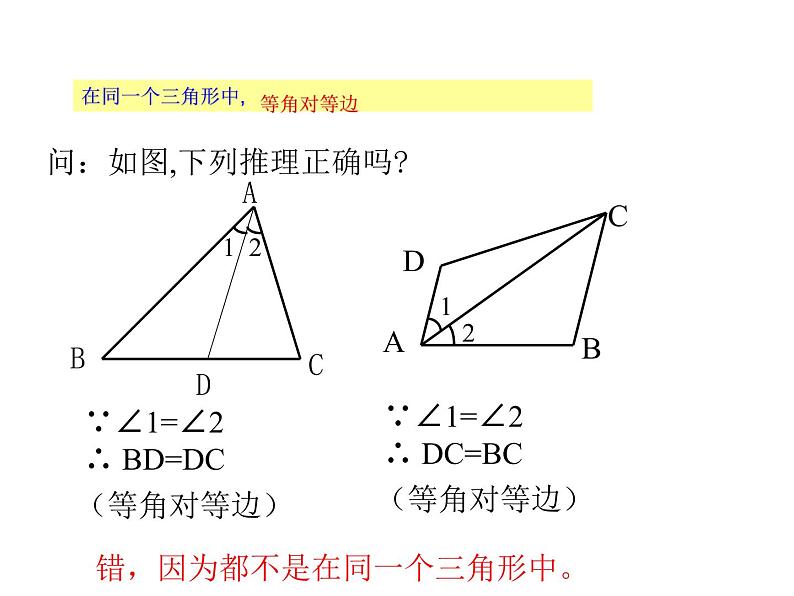
问:如图,下列推理正确吗?
错,因为都不是在同一个三角形中。
1.在△ABC中, 已知∠A=40°,∠B=70°,判断△ABC是什么三角形,为什么?
答:等腰三角形。理由:∵∠A=40° ,∠B=70° ∴ ∠C=180°- ∠A- ∠B=180°-40°-70°=70°∴ ∠B= ∠C ∴ △ABC是等腰三角形
2、已知:如图(2),∠A=36°, ∠DBC=36°, ∠C=72°,计算∠1和∠2的度数,并说明图中有哪些是等腰三角形。
2.如图,在△ABC中,D、E分别是AB、AC上的点,DE∥BC,∠1= ∠2。说明△ABC的等腰三角形的理由.
变2. 已知:如图,DE∥BC,∠1=∠2.求证:BD=CE.
∴AD=AE(在同一个三角形中,等角对等边)
∴∠1=∠B,∠2=∠C
∴AB=AC(在同一个三角形中,等角对等边)
∴AB-AD=AE-AC
例:一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°.量出AC的长,它就是河宽(即A,B之间的距离).这个方法正确吗?请说明理由.
1、说明线段所在的两个三角形全等。
2、说明同一个三角形中线段所对的两个角相等。
解: ∵ ∠ DAC= ∠ C+ ∠ ABC(三角形外角和的性质)
∴ ∠ ABC= ∠ DAC -∠ ACB=60 °- 30 ° =30 °
∴ ∠ ABC= ∠ C
∴ AB=AC(在同一个三角形中, 等角对等边)
想一想:还有其它测量河宽的方法吗?
又 ∵ ∠ C=30 ° ∠ DAC= 60 °
(1)一个三角形还满足什么条件时会成为等边三角形?
①三个角都相等的三角形是等边三角形.
②有一个角等于60°的等腰三角形是等边三角形.
点拨:有一个角是60°,在等腰三角形中有两种情况:(1)这个角是底角;(2)这个角是顶角.
三条边都相等的三角形是等边三角形.
证明:三个角都相等的三角形是等边三角形.已知:△ABC中,∠A=∠B=∠C.求证:△ABC是等边三角形.证明:∵∠A=∠B, ∴BC=AC(在同一个三角形中,等角对等边). 又∵∠A=∠C, ∴BC=AB(在同一个三角形中,等角对等边). ∴AB=BC=CA, 即△ABC是等边三角形.
证明:∵AB=AC,∠B=60°(已知),∴∠C=∠B=60°(在同一个三角形中,等角对等边)∴∠A=60°(三角形内角和定理).∴∠A=∠B =∠C=60°. ∴△ABC是等边三角形(三个角都相等的三角形是等边三角形).
已知:如图,在△ABC中,AB=AC,∠B=60°.求证:△ABC是等边三角形.
第一种情况:有一个底角是60°;
证明:∵AB=AC,∠A=60°(已知),∴∠C=∠B=60°(在同一个三角形中,等角对等边) ∴∠A=∠B=∠C =60°,∴△ABC是等边三角形(三个角都相等的三角形是等边三角形).
第二种情况:顶角是60°;
已知:如图,在△ABC中,AB=AC,∠A=60°.求证:△ABC是等边三角形.
初中数学2.4 等腰三角形的判定定理多媒体教学ppt课件: 这是一份初中数学2.4 等腰三角形的判定定理多媒体教学ppt课件,共18页。PPT课件主要包含了探究新知,探究归纳,用文字语言表示为,用数学语言表示为,学以致用,例题探究,跟踪练习,课堂小结等内容,欢迎下载使用。
初中数学浙教版八年级上册2.3 等腰三角形的性质定理图文ppt课件: 这是一份初中数学浙教版八年级上册2.3 等腰三角形的性质定理图文ppt课件,共16页。PPT课件主要包含了两边相等,轴对称,回顾旧知,已知ABAC,探究新知,°或55º,或45°,试一试,等腰三角形的主要特征,总结反思等内容,欢迎下载使用。
初中数学浙教版八年级上册2.3 等腰三角形的性质定理教课ppt课件: 这是一份初中数学浙教版八年级上册2.3 等腰三角形的性质定理教课ppt课件,共17页。PPT课件主要包含了想一想,AB≠AC等内容,欢迎下载使用。













