
初中数学2.3 等腰三角形的性质定理导学案
展开A组
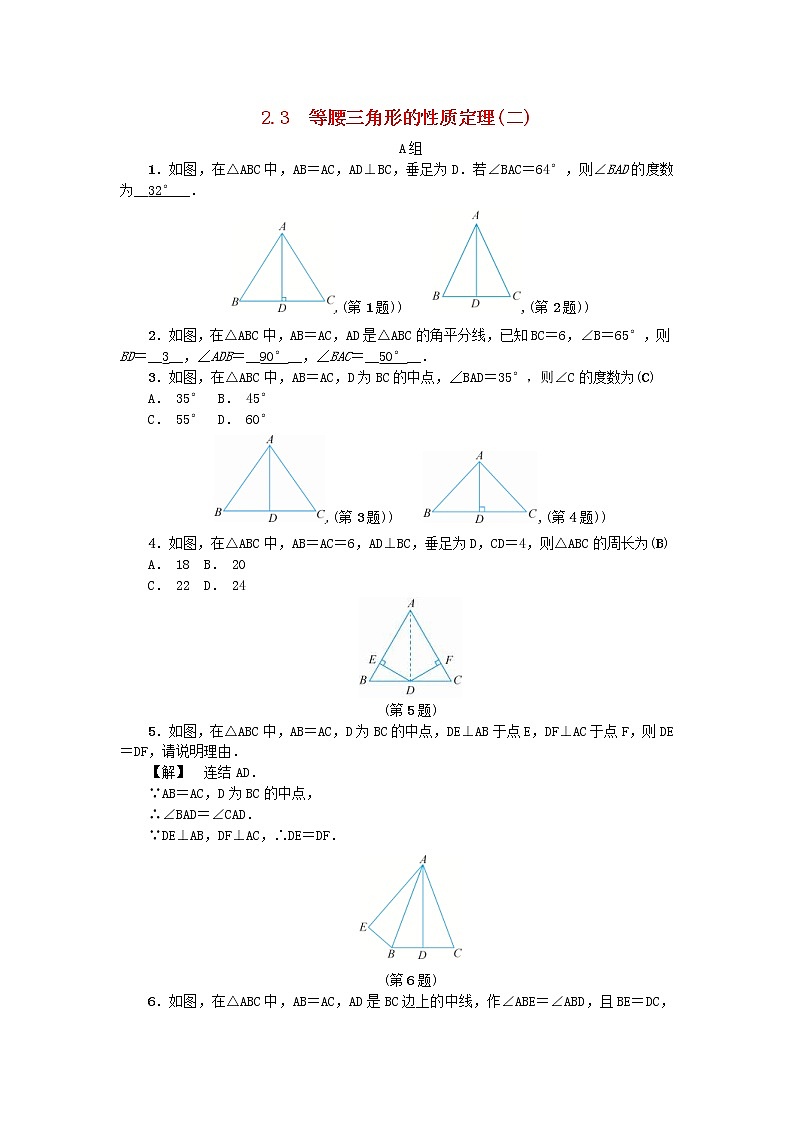
1.如图,在△ABC中,AB=AC,AD⊥BC,垂足为D.若∠BAC=64°,则∠BAD的度数为__32°__.
,(第1题)) ,(第2题))
2.如图,在△ABC中,AB=AC,AD是△ABC的角平分线,已知BC=6,∠B=65°,则BD=__3__,∠ADB=__90°__,∠BAC=__50°__.
3.如图,在△ABC中,AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为(C)
A. 35° B. 45°
C. 55° D. 60°
,(第3题)) ,(第4题))
4.如图,在△ABC中,AB=AC=6,AD⊥BC,垂足为D,CD=4,则△ABC的周长为(B)
A. 18 B. 20
C. 22 D. 24
(第5题)
5.如图,在△ABC中,AB=AC,D为BC的中点,DE⊥AB于点E,DF⊥AC于点F,则DE=DF,请说明理由.
【解】 连结AD.
∵AB=AC,D为BC的中点,
∴∠BAD=∠CAD.
∵DE⊥AB,DF⊥AC,∴DE=DF.
(第6题)
6.如图,在△ABC中,AB=AC,AD是BC边上的中线,作∠ABE=∠ABD,且BE=DC,连结AE.求证:AB平分∠EAD.
【解】 ∵AB=AC,AD是BC边上的中线,
∴BD=DC,AD⊥BC.
又∵BE=DC,∴BD=BE.
又∵∠ABD=∠ABE,AB=AB,
∴△ABD≌△ABE(SAS),
∴∠BAD=∠BAE,
即AB平分∠EAD.
(第7题)
7.如图,在等腰三角形ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG分别交AD,AC于点E,G,EF⊥AB,垂足为F.求证:EF=ED.
【解】 ∵AB=AC,AD是BC边上的中线,∴AD⊥BC.
又∵BG平分∠ABC,EF⊥AB,∴EF=ED.
B组
(第8题)
8.如图,D,E分别是△ABC的边BC,AC上的点,若AB=AC,AD=AE,则(B)
A. 当∠B为定值时,∠CDE为定值
B. 当α为定值时,∠CDE为定值
C. 当β为定值时,∠CDE为定值
D. 当γ为定值时,∠CDE为定值
【解】 ∵AB=AC,∴∠B=∠C.
∵AD=AE,∴∠ADE=∠AED=γ.
∵∠AED=∠C+∠CDE,∠ADC=∠B+α,
即γ=∠C+∠CDE,γ+∠CDE=∠B+α,
∴2∠CDE=α.
9.如图,∠BOC=9°,点A在OB上,且OA=1,按以下要求画图:以点A为圆心,1为半径向右画弧交OC于点A1,得第一条线段AA1;再以点A1为圆心,1为半径向右画弧交OB于点A2,得第二条线段A1A2;再以点A2为圆心,1为半径向右画弧交OC于点A3,得第三条线段A2A3……这样一直画下去,最多能画__9__条线段.
(第9题)
【解】 由题意可知:AO=A1A,A1A=A2A1,…,
则∠AOA1=∠OA1A,∠A1AA2=∠A1A2A,….
∵∠BOC=9°,∴∠A1AB=2∠BOC=18°.
同理可得∠A2A1C=27°,∠A3A2B=36°,∠A4A3C=45°,∠A5A4B=54°,∠A6A5C=63°,∠A7A6B=72°,∠A8A7C=81°,∠A9A8B=90°,
∴第10个三角形将有两个底角等于90°,不符合三角形的内角和定理,故最多能画9条线段.
10.如图,在△ABC中,AB=AC,D是BC的中点,BF⊥AC于点F,交AD于点E,∠BAC=45°.求证:△AEF≌△BCF.
(第10题)
【解】 过点F作FG⊥AB于点G.
∵∠BAC=45°,BF⊥AF,
∴∠ABF=45°.
∵FG⊥AB,
∴∠AGF=∠BGF=90°.
在△AGF和△BGF中,
∵eq \b\lc\{(\a\vs4\al\c1(∠GAF=∠GBF=45°,,∠AGF=∠BGF,,GF=GF,))
∴△AGF≌△BGF(AAS),
∴AF=BF.
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∴∠EAF+∠C=90°.
∵BF⊥AC,
∴∠AFE=∠BFC=90°,∠CBF+∠C=90°,
∴∠EAF=∠CBF.
在△AEF和△BCF中,
∵eq \b\lc\{(\a\vs4\al\c1(∠EAF=∠CBF,,AF=BF,,∠AFE=∠BFC,))
∴△AEF≌△BCF(ASA).
(第11题)
11.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F.
(1)求证:DE=DF.
(2)问:如果DE,DF分别是∠ADB,∠ADC的平分线,那么它们还相等吗?
【解】 (1)∵AB=AC,AD⊥BC,
∴AD平分∠BAC.
∵DE⊥AB,DF⊥AC,
∴DE=DF.
(2)相等.理由如下:
由(1)知AD⊥BC,∠DAE=∠DAF,
∴∠ADB=∠ADC=90°.
∵DE,DF分别是∠ADB,∠ADC的平分线,
∴∠ADE=eq \f(1,2)∠ADB,∠ADF=eq \f(1,2)∠ADC,
∴∠ADE=∠ADF.
在△ADE和△ADF中,
∵eq \b\lc\{(\a\vs4\al\c1(∠DAE=∠DAF,,AD=AD,,∠ADE=∠ADF,))
∴△ADE≌△ADF(ASA),
∴DE=DF.
数学乐园
(第12题)
12.如图,在等腰三角形ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线相交于点O,点C沿EF折叠后与点O重合,求∠CEF的度数.
【解】 连结BO.
∵∠BAC=50°,∠BAC的平分线与AB的中垂线相交于点O,
∴∠OBA=∠OAB=eq \f(1,2)∠BAC=25°.
∵AB=AC,∠BAC=50°,
∴∠ABC=∠ACB=65°.
∴∠OBC=65°-25°=40°.
根据等腰三角形的对称性,得∠OCB=∠OBC=40°.
∵点C沿EF折叠后与点O重合,
∴EO=EC,∠CEF=∠OEF,
∴∠EOC=∠ECO=40°,
∴∠CEF=∠OEF=eq \f(180°-2×40°,2)=50°.
初中数学浙教版八年级上册第2章 特殊三角形综合与测试导学案: 这是一份初中数学浙教版八年级上册第2章 特殊三角形综合与测试导学案,共13页。学案主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
浙教版八年级上册2.7 探索勾股定理学案设计: 这是一份浙教版八年级上册2.7 探索勾股定理学案设计,共5页。
浙教版八年级上册2.7 探索勾股定理导学案: 这是一份浙教版八年级上册2.7 探索勾股定理导学案,共4页。













