




初中数学浙教版八年级上册1.3 证明教学演示课件ppt
展开第1章 三角形的初步认识1.3 证明(1)
现阶段我们在数学上学习的命题由几类?
(包括定义、公理和定理)
判定一个命题是真命题的方法:
(1)通过推理的方式,即根据已知的事实来推断未知事实;
(2)人们经过长期实践后而公认为正确的.
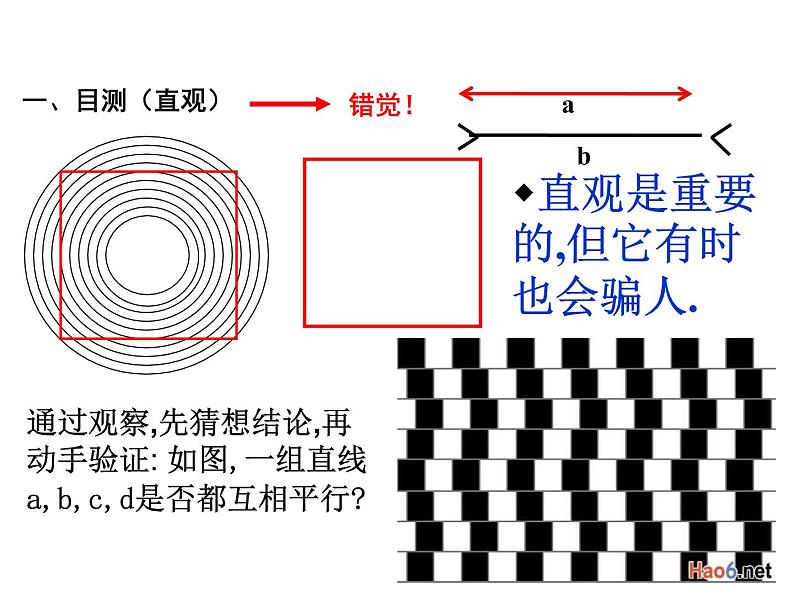
通过观察,先猜想结论,再动手验证: 如图,一组直线a,b,c,d是否都互相平行?
直观是重要的,但它有时也会骗人.
如何判断一个命题是真命题?
当n=6时, n2-3n+7 =25不是素数
当n=0,1,2,3,4时,代数式n2-3n+7的值分别是7,5,5,7,11,它们都是素数.那么,命题“对于自然数n,代数式n2-3n+7的值都是素数”是真命题吗?
四、判定一个命题是真命题的方法:
通过推理的方式,即根据已知的事实来推断未知事实;
要判定一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、基本事实、定理,一步一步推得结论成立,这样的推理过程叫做 证明 。
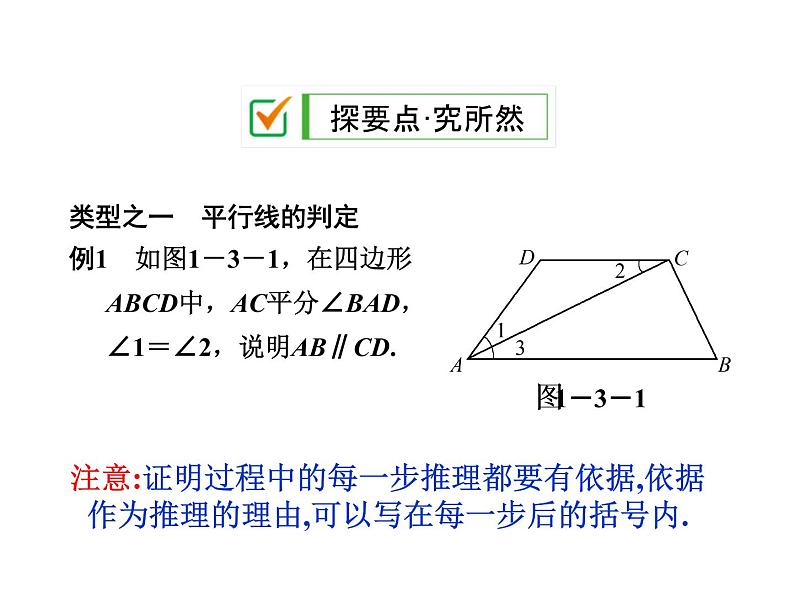
类型之一 平行线的判定例1 如图1-3-1,在四边形ABCD中,AC平分∠BAD,∠1=∠2,说明AB∥CD.
注意:证明过程中的每一步推理都要有依据,依据 作为推理的理由,可以写在每一步后的括号内.
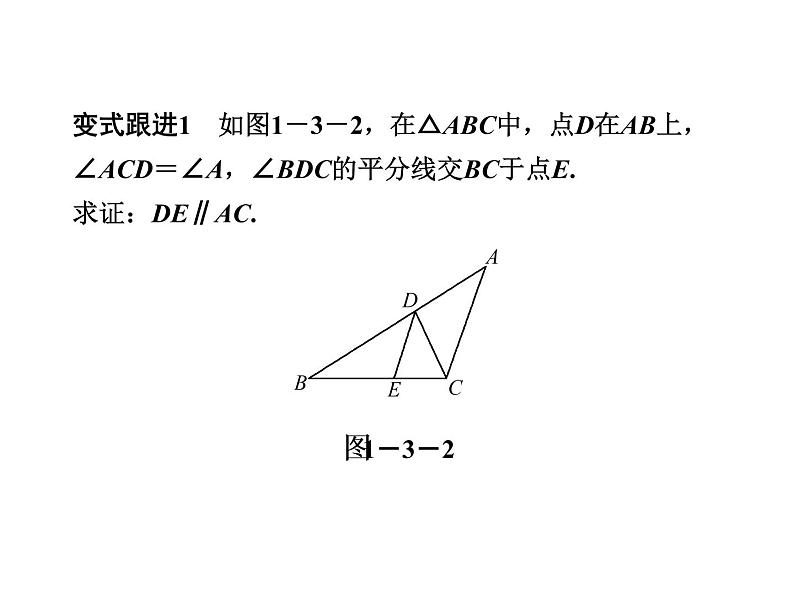
变式跟进1 如图1-3-2,在△ABC中,点D在AB上,∠ACD=∠A,∠BDC的平分线交BC于点E.求证:DE∥AC.
证明:∵∠BDE+∠CDE=180°-∠ADC=∠A+∠ACD,又∵DE是∠BDC的平分线,∠ACD=∠A,∴∠A=∠BDE,∴DE∥AC(同位角相等,两直线平行).
类型之二 平行线的性质例2 如图1-3-3,直线AB∥CD,直线EF分别交AB,CD于点M,N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠1的度数.
【解析】 根据角平分线的定义,两直线平行内错角相等的性质解答.解:∵∠EMB=50°,∴∠BMF=180°-∠EMB=130°.∵AB∥CD,∴∠1=∠BMG=65°.
变式跟进2 [2014·德州]如图1-3-4,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为 ( )A.30° B.60° C.80° D.120°
变式跟进3 如图1-3-5,AB∥CD,直线EF分别交AB,CD于点E,F,EG平分∠AEF,∠1=40°,求∠2的度数.
解:∵AB∥CD,∴∠1=∠AEG.∵EG平分∠AEF,∴∠1=∠GEF,∠AEF=2∠1.又∵∠AEF+∠2=180°,∴∠2=180°-2∠1=180°-80°=100°.
类型之三 平行线的判定与性质的综合例3 如图1-3-6,∠A=∠C,∠1和∠2互补,那么AB与CD是否平行?请说明理由.
解:∵∠1和∠2互补,∴AD∥BC,∴∠C+∠ADC=180°,又∵∠A=∠C,∴∠A+∠ADC=180°,∴AB∥CD.
变式跟进4 请将下列证明过程补充完整.已知:如图1-3-7,AD⊥BC,EF⊥BC,垂足分别为D,F,∠EGA=∠E.求证:AD平分∠BAC.
证明:∵AD⊥BC,EF⊥BC(已知),∴∠EFC=∠ADC=90°(垂直的定义).∴_______∥ _______.∴ __________= _________(两直线平行,内错角相等), __________= _________(两直线平行,同位角相等).∵ __________= _________(已知),∴ _____________________,∴AD平分∠BAC(____________________).
第2课时 三角形的内角和定理及推论
对于三角形,我们已经有哪些认识?
1.三角形的内角和性质:三角形三个内角的和等于_________.2.三角形的外角定义:由三角形一条边的延长线和另一条相邻的边组成的角.性质1:三角形的一个外角等于与它不相邻的两个___________.性质2:三角形的一个外角大于与它不相邻的任何一个内角.
三角形的三个内角的和等于180°.
如图,∠A,∠B,∠C是△ABC的三个内角.
∠A+∠B+∠C=180°
实验1:先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图1),然后把另处两角相向对折,使其顶点与已折角的顶点相嵌合(图2)、(图3),最后得到(图4)所示的结果。
例1、求证:三角形三个内角的和等于180º.
实验2: 将纸片三角形顶角剪下,随意将它们拼凑在一起。
在证明三角形内角和时,小明的想法是把三个角“凑”到A处,他过点A作直线DE//BC,(如图)。他的想法可行吗?
证明 过点A作DE∥BC.则∠C=∠CAE,∠B=∠BAD(两直线平行,内错角相等)∴∠BAC+∠B+∠C=∠BAC+∠BAD+∠CAE =∠DAE=180º(平角的定义)
你还有其他的证明方法么?
3.证明几何命题的格式格式:(1)按照题意画出图形;(2)分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论;(3)在“证明”中写出推理过程.
类型之一 三角形的内角和的运用例1 如图1-3-12,△ABC中,∠A=60°,∠B∶∠C=1∶5.求∠B的度数.
变式跟进1 如图1-3-13,△ABC中,∠B=50°,∠C=60°,点D是BC边上的任意一点,DE⊥AB于E,DF⊥AC于F,那么∠EDF等于 ( )A.80° B.110°C.130° D.140°
变式跟进2 如图1-3-14,AD是△ABC的高,BE平分∠ABC交AD于O,∠BAC=50°,∠C=54°.求:∠AEB和∠AOB的度数.
解:∵∠BAC=50°,∠C=54°,∴∠ABC=180°-∠C-∠BAC=76°,∵BE平分∠ABC,在△ABE中,∠AEB=180°-∠BAC-∠ABE=180°-50°-38°=92°,∵AD是高线,∠ABD=76°,∴∠BAD=14°.在△OBA中,∠AOB=180°-∠BAO-∠ABO.∴∠AOB=128°.综上,∠AEB=92°,∠AOB=128°.
类型之二 三角形的外角性质应用例2 星期天,小明见爸爸愁眉苦脸地在看一张图纸,他便悄悄地来到爸爸身边,想看爸爸为什么犯愁.爸爸见到他,高兴地对他说:“来帮我一个忙,你看这是一个四边形零件的平面图,它要求∠BDC等于140°才算合格.”小明通过测量得∠A=90°,∠B=19°,∠C=40°后就下结论说此零件不合格,于是爸爸让小明解释这是为什么,小明很轻松地说出了原因,并用如下的两种方法解出此题.请你代小明分别说出不合格的理由.
(1)如图1-3-15(1),连结AD并延长;(2)如图1-3-15(2),延长CD交AB于E.
【解析】 直接利用各个三角形中的外角和等于与它不相邻的两个内角和求解.解:(1)∠BDC=∠1+∠2=∠A+∠B+∠C=90°+19°+40°=149°≠140°,故不合格;(2)∠BDC=∠1+∠B=∠A+∠C+∠B=149°≠140°,故不合格.
【点悟】 (1)三角形的外角等于与它不相邻的两个内角和.(2)三角形的内角和是180°.求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件.
变式跟进3 如图1-3-16,AB∥CD,∠E=37°,∠C=20°,则∠EAB的度数为 ( )A.57° B.60° C.63° D.123°
变式跟进4 如图1-3-17,l1∥l2,∠α=______度.【解析】 ∵l1∥l2,∴∠1=120°,∵∠2=∠1,∴∠α=180°-∠2-25°=35°.
变式跟进5 如图1-3-18,∠A+∠B+∠C+∠D+∠E=__________.
初中数学浙教版八年级上册第1章 三角形的初步知识1.3 证明教学演示ppt课件: 这是一份初中数学浙教版八年级上册第1章 三角形的初步知识1.3 证明教学演示ppt课件,共19页。PPT课件主要包含了教学目标,证明思路,由“因”导“果”,执“果”索“因”,步步有据,证明步骤,按题意画出图形,内角和,例3求证,=180º等内容,欢迎下载使用。
初中数学浙教版八年级上册第1章 三角形的初步知识1.3 证明背景图ppt课件: 这是一份初中数学浙教版八年级上册第1章 三角形的初步知识1.3 证明背景图ppt课件,共19页。PPT课件主要包含了教学目标,真命题,假命题,举反例,定义公理已证明的定理,推理的依据,问题情境1,线段ab相等吗,问题情境2,问题情境3等内容,欢迎下载使用。
初中数学浙教版八年级上册第1章 三角形的初步知识1.3 证明说课课件ppt: 这是一份初中数学浙教版八年级上册第1章 三角形的初步知识1.3 证明说课课件ppt,共11页。PPT课件主要包含了说一说,∠1∠A+∠B,小试牛刀1,小试牛刀2,练一练,试一试,想一想等内容,欢迎下载使用。













