人教版八年级上册第十一章 三角形综合与测试课后测评

这是一份人教版八年级上册第十一章 三角形综合与测试课后测评，共13页。




一．选择题


1．下列各组长度的三条线段能组成三角形的是（ ）


A．1，2，3B．1，1，2C．1，2，2D．1，5，7


2．已知，在△ABC中，∠B是∠A的3倍，∠C比∠A大30°，则∠A的度数是（ ）


A．30°B．50°C．70°D．90°


3．如图，在△ABC中，BC边上的高为（ ）





A．ADB．BEC．BFD．CG


4．如图，△ABC中，∠A＝40°，将△ABC沿DE折叠，点A落在F处，则∠FDB+∠FEC的度数为（ ）





A．140°B．120°C．70°D．80°


5．一个多边形的内角和比它的外角和的2倍还大180°，这个多边形的边数为（ ）


A．7B．8C．9D．10


6．如果多边形的内角和是外角和的k倍，那么这个多边形的边数是（ ）


A．kB．2k+1C．2k+2D．2k﹣2


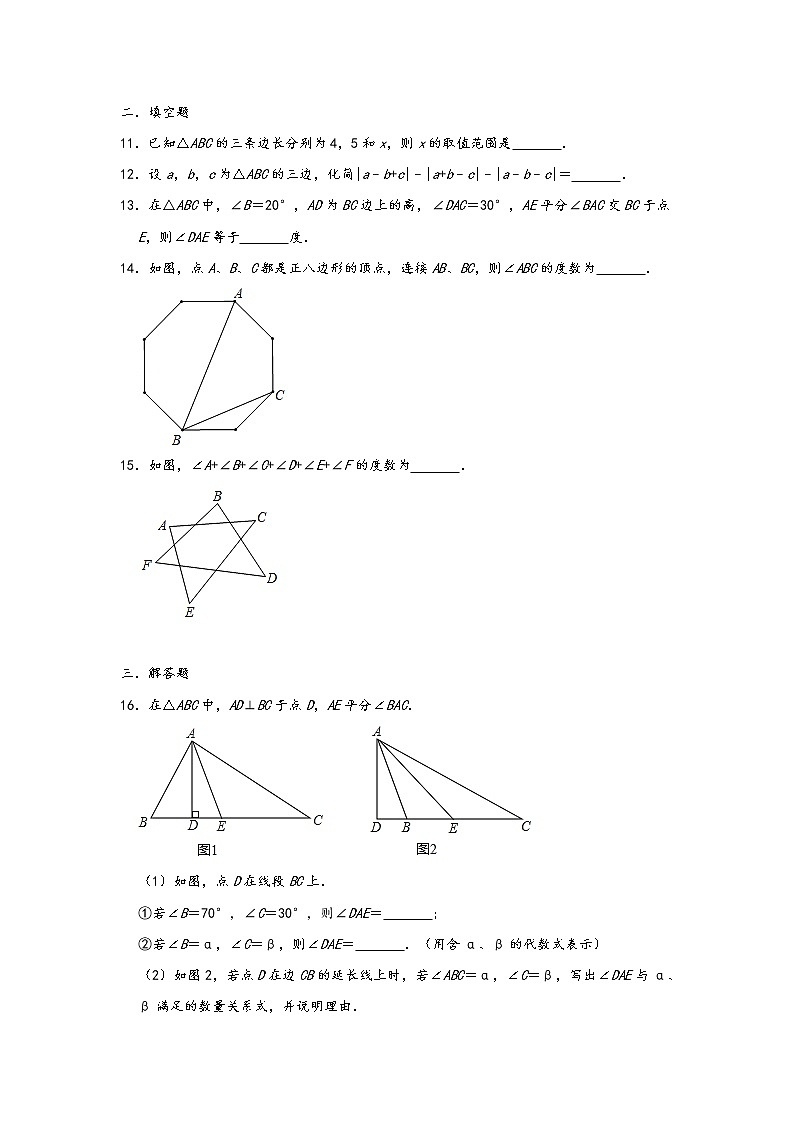
7．如图，AD是△ABC的角平分线，点O在AD上，且OE⊥BC于点E，∠BAC＝60°，∠C＝80°，则∠EOD的度数为（ ）





A．20°B．30°C．10°D．15°


8．如图，小丽画了一个三角形，不小心被墨水污染了，只剩下一个角（锐角）．小丽画的三角形可能是（ ）





A．锐角三角形B．直角三角形


C．钝角三角形D．以上都有可能


9．为了使一扇旧木门不变形，木工师傅在木门的背面加钉了一根木条，这样做的道理是（ ）





A．两点之间，线段最短


B．垂线段最短


C．三角形具有稳定性


D．两直线平行，内错角相等


10．如下图，BE是∠ABD的角平分线，CF是∠ACD的角平分线，BE与CF交于点G，点∠BDC＝140°，∠BGC＝110°，则∠A的度数为（ ）





A．70°B．75°C．80°D．85°





二．填空题


11．已知△ABC的三条边长分别为4，5和x，则x的取值范围是 ．


12．设a，b，c为△ABC的三边，化简|a﹣b+c|﹣|a+b﹣c|﹣|a﹣b﹣c|＝ ．


13．在△ABC中，∠B＝20°，AD为BC边上的高，∠DAC＝30°，AE平分∠BAC交BC于点E，则∠DAE等于 度．


14．如图，点A、B、C都是正八边形的顶点，连接AB、BC，则∠ABC的度数为 ．





15．如图，∠A+∠B+∠C+∠D+∠E+∠F的度数为 ．








三．解答题


16．在△ABC中，AD⊥BC于点D，AE平分∠BAC．





（1）如图，点D在线段BC上．


①若∠B＝70°，∠C＝30°，则∠DAE＝ ；


②若∠B＝α，∠C＝β，则∠DAE＝ ．（用含α、β的代数式表示）


（2）如图2，若点D在边CB的延长线上时，若∠ABC＝α，∠C＝β，写出∠DAE与α、β满足的数量关系式，并说明理由．


17．△ABC中，∠C＝80°，点D、E分别是△ABC边AC、BC上的点，点P是一动点，令∠PDA＝∠1，∠PEB＝∠2，∠DPE＝∠α．．


（1）若点P在边AB上，且∠α＝50°，如图1，则∠1+∠2＝ ；


（2）若点P在边AB上运动，如图2所示，则∠α、∠1、∠2之间的关系为 ．


（3）若点P运动到边AB的延长线上，如图3，则∠α、∠1、∠2之间有何关系？猜想并说明理由








18．如图，在△ABC中，∠B＝40°，∠C＝70°，AD是△ABC的角平分线，点E在BD上，点F在CA的延长线上，EF∥AD．


（1）求∠BAF的度数．


（2）求∠F的度数．














19．四边形ABCD中，∠BAD的角平分线与边BC交于点E，∠ADC的角平分线交直线AE于点O．


（1）若点O在四边形ABCD的内部，


①如图1，若AD∥BC，∠B＝40°，∠C＝70°，则∠DOE＝ °；


②如图2，试探索∠B、∠C、∠DOE之间的数量关系，并将你的探索过程写下来．


（2）如图3，若点O在四边形ABCD的外部，请你直接写出∠B、∠C、∠DOE之间的数量关系．

















20．直线MN与直线PQ垂直相交于O，点A在射线OP上运动，点B在射线OM上运动．


（1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值；


（2）如图2，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线相交于E、F，则∠EAF＝ °；在△AEF中，如果有一个角是另一个角的3倍，试求∠ABO的度数．








参考答案


一．选择题


1．解：A.1+2＝3，不能构成三角形，不合题意；


B.1+1＝2，不能构成三角形，不合题意；


C..1+2＞2，能构成三角形，符合题意；


D.1+5＜7，不能构成三角形，不合题意．


故选：C．


2．解：由题意，


解得，


故选：A．


3．解：由图可知，△ABC中，BC边上的高为AD，


故选：A．


4．解：∵∠A＝40°，


∴∠ADE+∠AED＝180°﹣∠A＝140°，


由折叠知，∠ADE＝∠FDE，∠AED＝∠FED，


∴∠ADF+∠AEF＝2（∠ADE+∠AED）＝280°，


∵∠FDB+∠FEC＝180°﹣∠ADF+180°﹣∠AEF＝360°﹣280°＝80°，


故选：D．


5．解：设这个多边形的边数为n，


根据题意得，（n﹣2）•180°＝360°×2+180°，


解得n＝7．


故选：A．


6．解：设这个多边形的边数是n，


则（n﹣2）•180°＝k•360°，


解得n＝2k+2．


故选：C．


7．解：∵∠BAC＝60°，∠C＝80°，


∴∠B＝40°．


又∵AD是∠BAC的角平分线，


∴∠BAD＝∠BAC＝30°，


∴∠ADE＝70°，


又∵OE⊥BC，


∴∠EOD＝20°．


故选：A．


8．解：∵此三角形只知道一个角为锐角，其他角可能有钝角或直角也可能是都是锐角，


∴三角形可能为：A、锐角三角形；B、直角三角形；C、钝角三角形都有可能．


故选：D．


9．解：这样做的道理是三角形具有稳定性．


故选：C．


10．解：如图，连接BC．


BE是∠ABD的平分线，CF是∠ACD的平分线，


∴∠ABE＝∠DBE＝∠ABD，∠ACF＝∠DCF＝∠ACD，


又∠BDC＝140°，∠BGC＝110°，


∴∠DBC+∠DCB＝40°，∠GBC+∠GCB＝70°，


∴∠EBD+∠FCD＝70°﹣40°＝30°，


∴∠ABE+∠ACF＝30°，


∴∠ABE+∠ACF+∠GBC+∠GCB＝70°+30°＝100°，即∠ABC+∠ACB＝100°，


∴∠A＝80°．


故选：C．





二．填空题（共5小题）


11．解：∵三角形的两边长分别为4和5，


∴第三边长x的取值范围是：5﹣4＜x＜5+4，


即：1＜x＜9，


故答案为：1＜x＜9．


12．解：∵a，b，c为△ABC的三边，


∴a﹣b+c＞0，a+b﹣c＞0，a﹣b﹣c＜0，


∴|a﹣b+c|﹣|a+b﹣c|﹣|a﹣b﹣c|＝a﹣b+c﹣（a+b﹣c）+（a﹣b﹣c）


＝a﹣b+c﹣a﹣b+c+a﹣b﹣c


＝a﹣3b+c．


故答案为：a﹣3b+c．


13．解：有两种情况：①当∠BAC是钝角时，如图：


∵AD为BC边上的高，


∴∠ADC＝90°，


∵∠DAC＝30°，


∴∠ACB＝60°，


∵∠ABC＝20°，


∴∠BAC＝180°﹣∠ABC﹣∠ACB＝100°，


∵AE平分∠BAC，


∴∠CAE＝BAC＝50°，


∴∠DAE＝∠CAE﹣∠CAD＝50°﹣30°＝20°；


②当∠BAC是锐角时，如图：


∵AD为BC边上的高，


∴∠ADC＝90°，


∵∠DAC＝30°，


∴∠ACD＝60°，


∴∠ACB＝180°﹣60°＝120°，


∵∠ABC＝20°，


∴∠BAC＝180°﹣∠ABC﹣∠ACB＝40°，


∵AE平分∠BAC，


∴∠CAE＝BAC＝20°，


∴∠DAE＝∠CAE+∠CAD＝20°+30°＝50°；


故答案为：20或50．


14．解：如图，





∵正八边形的每个内角的度数为：＝135°，


∴∠CBD＝＝22.5°，＝67.5°，


∴∠ABC＝∠ABD﹣∠CBD＝67.5°﹣22.5°＝45°．


故答案为：45°．


15．解：在△ACE和△BDF中，


∠A+∠C+∠E＝180°，∠B+∠D+∠F＝180°，


∴∠A+∠B+∠C+∠D+∠E+∠F＝180°+180°＝360°，


故答案为：360°．


三．解答题（共5小题）


16．解：（1）①∵∠B＝70°，∠C＝30°，


∴∠BAC＝180°﹣70°﹣30°＝80°，


∵AE平分∠BAC，


∴，


∴∠AED＝∠C+∠EAC＝70°，


∴∠DAE＝90°﹣∠AED＝20°．


②∵∠B＝α，∠C＝β，


∴∠BAC＝180°﹣α﹣β，


∵AE平分∠BAC，


∴∠EAC＝90°﹣α﹣β，


∴∠DAE＝90°﹣∠AED＝90°﹣（∠C+∠EAC）＝＝．


故答案为：①20°，②；


（2）∠DAE＝．


理由：∵∠DAB+∠D＝∠ABC，


∴∠DAB＝∠ABC﹣∠D＝α﹣90°，


∵AE平分∠BAC，


∴＝＝＝，


∵∠DAE＝∠DAB+∠BAE，


∴＝．


17．解：（1）如图1，连接CP，


∵∠1是△CDP的外角，


∴∠1＝∠DCP+∠DPC，


同理可得，∠2＝∠ECP+∠EPC，


∴∠1+∠2＝∠ACB+∠DPE＝80°+50°＝130°，





故答案为：130°；





（2）如图，连接CP，


∵∠1是△CDP的外角，


∴∠1＝∠DCP+∠DPC，


同理可得，∠2＝∠ECP+∠EPC，


∴∠1+∠2＝∠ACB+∠DPE＝80°+∠α，





故答案为：∠1+∠2＝80°+∠α；





（3）∠1＝80°+∠2+∠α，理由如下：





如图3，∵在△CDM中，∠1＝∠C+∠CMD，


在△EMP中，∠CMD＝∠2+∠α，


∴∠1＝∠C+∠2+∠α，


即∠1＝80°+∠2+∠α．


18．解：（1）∵∠BAF＝∠B+∠C，


∵∠B＝40°，∠C＝70°，


∴∠BAF＝110°；


（2）∵∠BAF＝110°，


∴∠BAC＝70°，


∵AD是△ABC的角平分线，


∴∠DAC＝BAC＝35°，


∵EF∥AD，


∴∠F＝∠DAC＝35°．


19．解：（1）①∵AD∥BC，∠B＝40°，∠C＝70°，


∴∠BAD＝140°，∠ADC＝110°，


∵AE、DO分别平分∠BAD、∠CDA，


∴∠OAD＝70°，∠ADO＝55°，


∴∠DOE＝∠OAD+∠ADO＝70°+55°＝125°


故答案为：125；





②∠B+∠C+2∠DOE＝360°，


理由：∵∠DOE＝∠OAD+∠ADO，


∵AE、DO分别平分∠BAD、∠CDA，


∴2∠DOE＝∠BAD+∠ADC，


∵∠B+∠C+∠BAD+∠ADC＝360°，


∴∠B+∠C+2∠DOE＝360°；





（2）∠B+∠C＝2∠DOE，


理由：∵∠BAD+∠ADC＝360°﹣∠B﹣∠C，∠EAD+∠ADO＝180°﹣∠DOE，


∵AE、DO分别平分∠BAD、∠CDA，


∴∠BAD＝2∠EAD，∠ADC＝2∠ADO，


∴∠BAD+∠ADC＝2（∠EAD+∠ADO），


∴360°﹣∠B﹣∠C＝2（180°﹣∠DOE），


∴∠B+∠C＝2∠DOE．


20．解：（1）∠AEB的大小不变，


∵直线MN与直线PQ垂直相交于O，


∴∠AOB＝90°，


∴∠OAB+∠OBA＝90°，


∵AE、BE分别是∠BAO和∠ABO角的平分线，


∴∠BAE＝∠OAB，∠ABE＝∠ABO，


∴∠BAE+∠ABE＝（∠OAB+∠ABO）＝×90°＝45°，


∴∠AEB＝135°；





（2）∵AE、AF分别是∠BAO和∠OAG的角平分线，


∴∠EAO＝∠BAO，∠FAO＝∠GAO，


∴∠EAF＝（∠BAO+∠GAO）＝×180°＝90°．


故答案为：90；


∵∠BAO与∠BOQ的角平分线相交于E，


∴∠EAO＝∠BAO，∠EOQ＝∠BOQ，


∴∠E＝∠EOQ﹣∠EAO＝（∠BOQ﹣∠BAO）＝∠ABO，


即∠ABO＝2∠E，


在△AEF中，∵有一个角是另一个角的3倍，故分四种情况讨论：


①∠EAF＝3∠E，∠E＝30°，则∠ABO＝60°；


②∠EAF＝3∠F，∠E＝60°，∠ABO＝120°（舍去）；


③∠F＝3∠E，∠E＝22.5°，∠ABO＝45°；


④∠E＝3∠F，∠E＝67.5°，∠ABO＝135°（舍去）．


∴∠ABO为60°或45°．